Pourquoi la moyenne est-elle importante en statistiques ?

La moyenne d’un ensemble de données représente la valeur moyenne de l’ensemble de données. Il est calculé comme suit :

Moyenne = Σx _i / n

où:

• Σ : Un symbole qui signifie « somme »
• x _i : La i ^ème observation dans un ensemble de données
• n : le nombre total d’observations dans l’ensemble de données

Par exemple, supposons que nous ayons l’ensemble de données suivant avec 11 observations :

Ensemble de données : 3, 4, 4, 6, 7, 8, 12, 13, 15, 16, 17

La moyenne de l’ensemble de données est calculée comme suit :

Moyenne = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9,54

En statistiques, la moyenne est importante pour les raisons suivantes :

1. La moyenne nous donne une idée de l’endroit où se trouve le « centre » d’un ensemble de données.

2. En raison de la façon dont elle est calculée, la moyenne contient une information provenant de chaque observation d’un ensemble de données.

L’exemple suivant illustre ces deux raisons.

Exemple : Calculer la moyenne d’un ensemble de données

Supposons que nous disposions d’un ensemble de données contenant le prix de vente de 10 000 maisons différentes dans une certaine ville.

Au lieu de regarder des milliers de lignes de données brutes , nous pouvons calculer la valeur moyenne pour comprendre rapidement le prix de vente moyen des maisons dans cette ville.

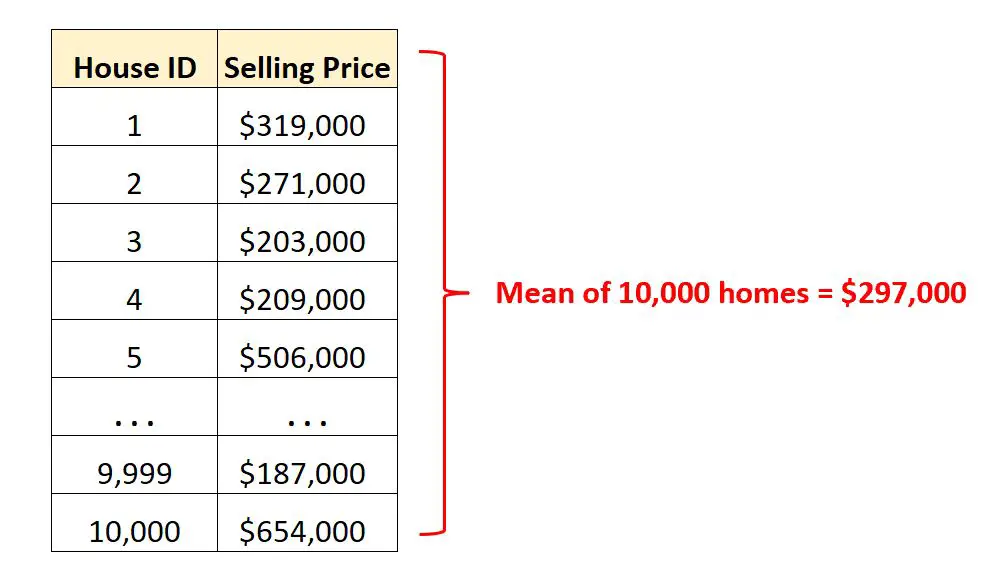
En sachant que le prix de vente moyen est de 297 000 $, on a une idée de ce à quoi se vend une maison « typique » dans cette ville.

Cette valeur unique de la moyenne est beaucoup plus facile à interpréter que de regarder toutes les lignes de données brutes.

Et puisque chaque prix de vente de maison a été utilisé pour calculer la moyenne, nous pourrions multiplier le prix de vente moyen par le nombre total de maisons pour trouver le prix de vente total de toutes les maisons de cette ville :

• Prix de vente total de toutes les maisons = Prix de vente moyen * Nombre de maisons
• Prix de vente total de toutes les maisons = 297 000 $ * 10 000
• Prix de vente total de toutes les maisons = 2 970 000 000 $

Nous pouvons voir que le prix de vente total de toutes les maisons de cette ville est de 2,97 milliards de dollars.

Quand utiliser la moyenne

Lors de l’analyse d’ensembles de données, nous souhaitons souvent comprendre où se situe la valeur centrale.

En statistiques, il existe deux métriques courantes que nous utilisons pour mesurer le centre d’un ensemble de données :

• Moyenne : la valeur moyenne dans un ensemble de données
• Médiane : La valeur médiane dans un ensemble de données

La moyenne est la manière la plus courante de mesurer le centre d’un ensemble de données, mais elle peut en réalité être trompeuse dans les situations suivantes :

• Quand la distribution est asymétrique .
• Lorsque la distribution contient des valeurs aberrantes .

Pour illustrer cela, considérons les deux exemples suivants.

Exemple 1 : Calcul de la moyenne d’une distribution asymétrique

Considérez la répartition suivante des salaires pour les résidents d’une certaine ville :

Les salaires élevés du côté droit de la distribution éloignent la moyenne du centre de la distribution.

Ainsi, la médiane rend mieux compte du salaire « typique » d’un résident que la moyenne, car la distribution est asymétrique vers la droite.

Dans cet exemple particulier, le salaire moyen est de 47 000 $ tandis que le salaire médian est de 32 000 $.

Ainsi, la médiane est beaucoup plus représentative du salaire type dans cette ville.

Exemple 2 : Calcul de la moyenne en présence de valeurs aberrantes

Considérez le graphique suivant qui montre la superficie en pieds carrés des maisons dans une certaine rue :

La moyenne est fortement influencée par quelques maisons extrêmement grandes, alors que la médiane ne l’est pas.

Nous pouvons voir que la médiane parvient mieux à capturer la superficie « typique » d’une maison dans cette rue que la moyenne, car elle n’est pas influencée par les valeurs extrêmes.

Résumé

Voici un bref résumé des principaux points à retenir de cet article :

• La moyenne représente la valeur moyenne dans un ensemble de données.
• La moyenne est importante car elle nous donne une idée de l’endroit où se situe la valeur centrale dans un ensemble de données.
• La moyenne est également importante car elle contient une information provenant de chaque observation d’un ensemble de données.
• La moyenne peut être trompeuse lorsqu’un ensemble de données est asymétrique ou contient des valeurs aberrantes. Dans ces scénarios, la médiane donne une idée plus précise de l’endroit où se trouve le « centre » d’un ensemble de données.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur d’autres statistiques descriptives :

Pourquoi la médiane est-elle importante dans les statistiques ?
Pourquoi l’écart type est-il important dans les statistiques ?
Quand utiliser la moyenne par rapport à la médiane