Distribution de Poisson ou distribution normale : quelle est la différence ?

La distribution de Poisson et la distribution normale sont deux des distributions de probabilité les plus couramment utilisées en statistique.

Ce didacticiel fournit une explication rapide de chaque distribution ainsi que deux différences clés entre les distributions.

Un aperçu : la distribution de Poisson

La distribution de Poisson décrit la probabilité d’obtenir k succès pendant un intervalle de temps donné.

Si une variable aléatoire X suit une distribution de Poisson, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = λ ^k * e ^{– λ} / k !

où:

• λ : nombre moyen de succès survenus au cours d’un intervalle spécifique
• k : nombre de réussites
• e : une constante égale à environ 2,71828

Par exemple, supposons qu’un hôpital particulier connaisse en moyenne 2 naissances par heure. Nous pouvons utiliser la formule ci-dessus pour déterminer la probabilité de connaître 3 naissances dans une heure donnée :

P(X=3) = 2 ³ * e ^{– 2} / 3 ! = 0,1805

La probabilité de connaître 3 naissances dans une heure donnée est de 0,1805 .

Un aperçu : la distribution normale

La distribution normale décrit la probabilité qu’une variable aléatoire prenne une valeur dans un intervalle donné.

La fonction de densité de probabilité d’une distribution normale peut s’écrire :

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

où:

• σ : Écart type de la distribution
• μ : Moyenne de la distribution
• x : valeur de la variable aléatoire

Par exemple, supposons que le poids d’une certaine espèce de loutres soit normalement distribué avec μ = 40 livres et σ = 5 livres.

Si nous sélectionnons au hasard une loutre dans cette population, nous pouvons utiliser la formule suivante pour trouver la probabilité qu’elle pèse entre 38 et 42 livres :

P(38 < X < 42) = (1/σ√ 2π )e ^{-1/2((42-40)/5) 2} – (1/σ√ 2π )e ^{-1/2((38-40) /5) 2} = 0,3108

La probabilité que la loutre sélectionnée au hasard pèse entre 38 et 42 livres est de 0,3108 .

Différence n°1 : données discrètes ou continues

La première différence entre la distribution de Poisson et la distribution normale réside dans le type de données modélisées par chaque distribution de probabilité.

Une distribution de Poisson est utilisée lorsque vous travaillez avec des données discrètes qui ne peuvent prendre que des valeurs entières égales ou supérieures à zéro. Voici quelques exemples :

• Nombre d’appels reçus par heure dans un centre d’appels
• Nombre de clients par jour dans un restaurant
• Nombre d’accidents de voiture par mois

Dans chaque scénario, la variable aléatoire ne peut prendre que la valeur 0, 1, 2, 3, etc.

Une distribution normale est utilisée lorsque vous travaillez avec des données continues pouvant prendre n’importe quelle valeur allant de l’infini négatif à l’infini positif. Voici quelques exemples :

• Poids d’un certain animal
• Hauteur d’une certaine plante
• Temps de marathon des femmes
• Température en Celsius

Dans ces scénarios, les variables aléatoires peuvent prendre n’importe quelle valeur comme -11,3, 21,343435, 85, etc.

Différence n°2 : forme des distributions

La deuxième différence entre la distribution de Poisson et la distribution normale réside dans la forme des distributions.

Une distribution normale présentera toujours une forme de cloche :

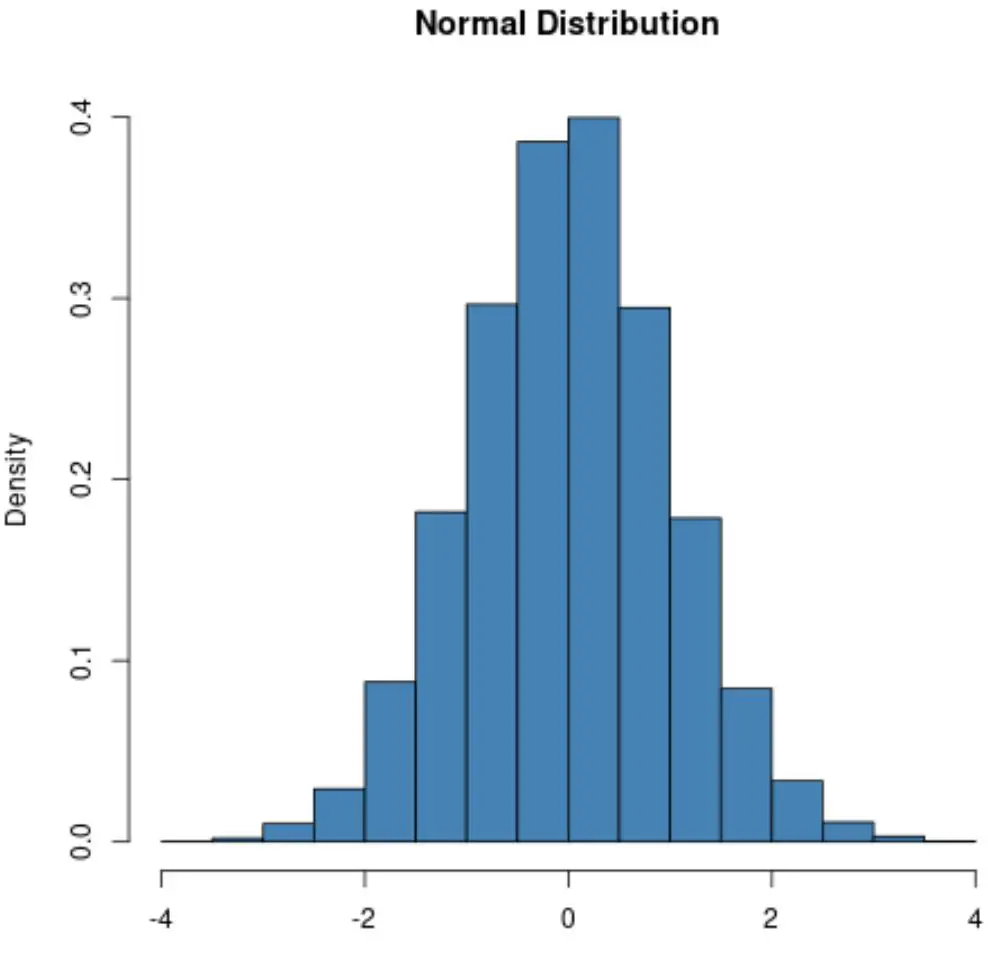
Cependant, la forme de la distribution de Poisson varie en fonction de la valeur moyenne de la distribution.

Par exemple, une distribution de Poisson avec une petite valeur pour la moyenne comme μ = 3 sera fortement asymétrique à droite :

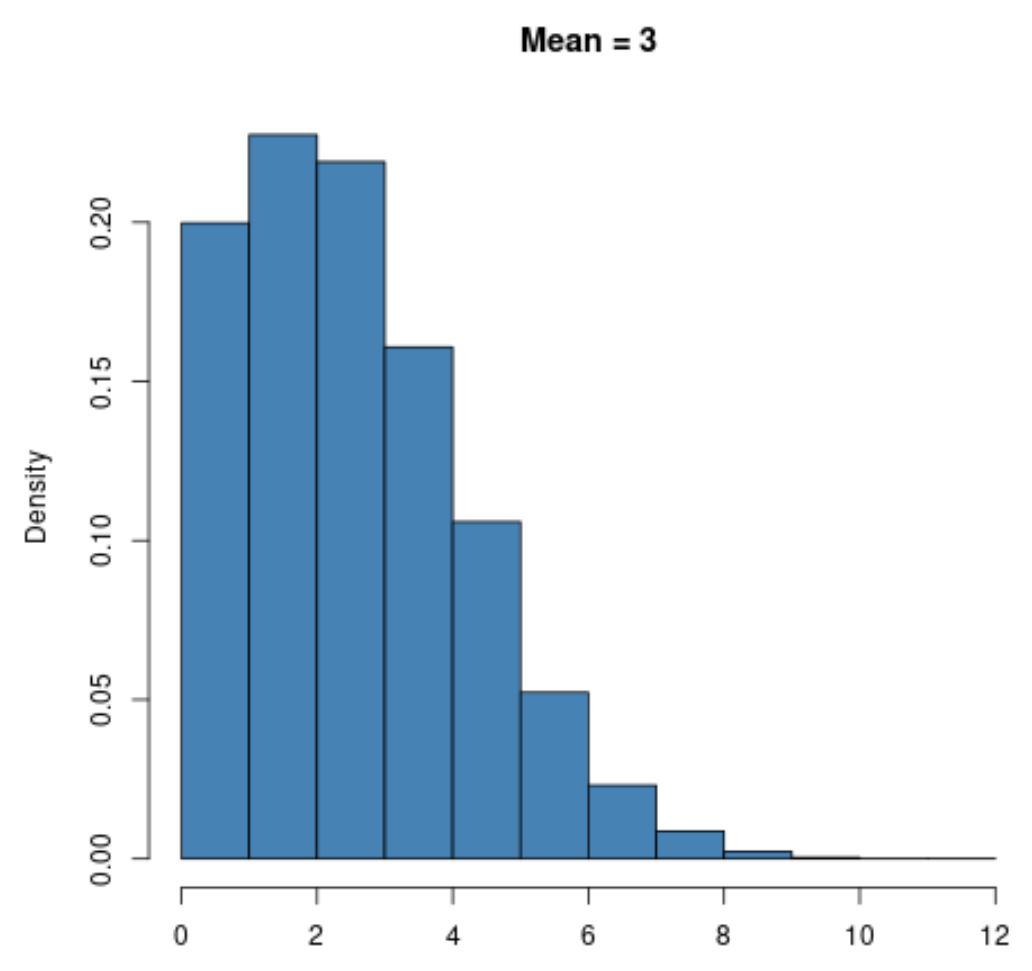
Cependant, une distribution de Poisson avec une valeur de moyenne plus grande comme μ = 20 présentera une forme de cloche tout comme la distribution normale :

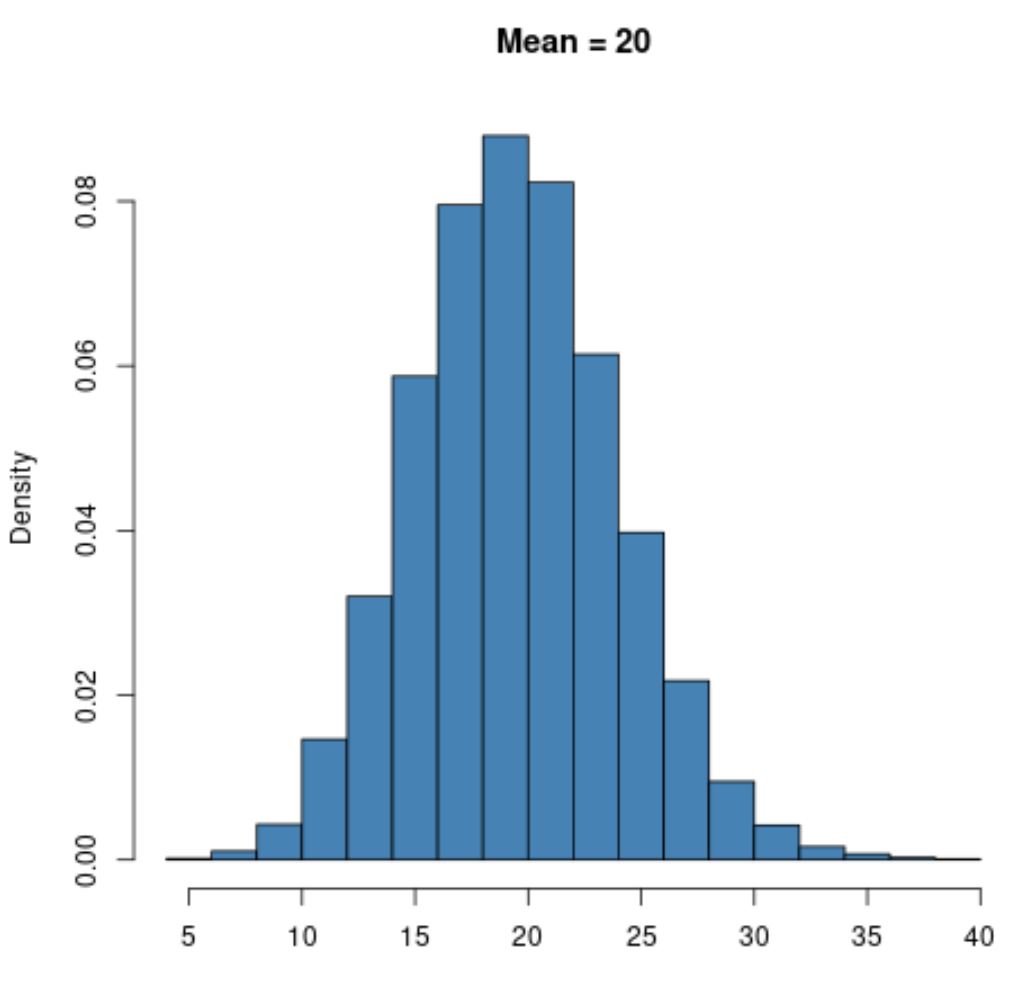
Notez que la limite inférieure d’une distribution de Poisson sera toujours nulle, quelle que soit la valeur de la moyenne, car une distribution de Poisson ne peut être utilisée qu’avec des valeurs entières égales ou supérieures à zéro.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la distribution de Poisson :

Une introduction à la distribution de Poisson
Les quatre hypothèses de la distribution de Poisson
5 exemples concrets de la distribution de Poisson

Les didacticiels suivants fournissent des informations supplémentaires sur la distribution normale :

Une introduction à la distribution normale
6 exemples concrets de la distribution normale
Générateur d’ensembles de données de distribution normale