Comment effectuer un test t sur un échantillon dans SAS
Un test t sur un échantillon est utilisé pour déterminer si la moyenne d’une population est égale ou non à une certaine valeur.
Ce didacticiel explique comment effectuer un test t sur un échantillon dans SAS.
Exemple : un échantillon de test t dans SAS
Supposons qu’un botaniste veuille savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces. Elle prélève un échantillon aléatoire de 12 plantes et enregistre chacune de leurs hauteurs en pouces.
Les hauteurs sont les suivantes : 14, 14, 16, 13, 12, 17, 15, 14, 15, 13, 15, 14
Utilisez les étapes suivantes pour effectuer un test t sur un échantillon afin de déterminer si la hauteur moyenne de cette espèce de plante est réellement égale à 15 pouces.
Étape 1 : Créez les données.
Tout d’abord, nous utiliserons le code suivant pour créer l’ensemble de données dans SAS :
/*create dataset*/ data my_data; input Height; datalines; 14 14 16 13 12 17 15 14 15 13 15 14 ; run; /*print dataset*/ proc print data=my_data;
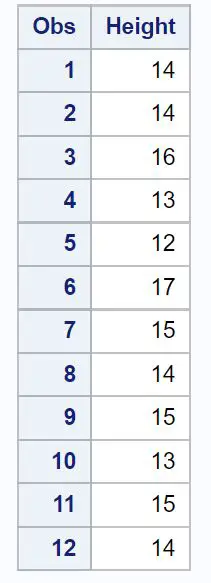
Étape 2 : Effectuez un test t sur un échantillon.
Ensuite, nous utiliserons proc ttest pour effectuer le test t sur un exemple :
/*perform one sample t-test*/ proc ttest data=my_data sides=2 alpha=0.05 h0=15; var Height; run;
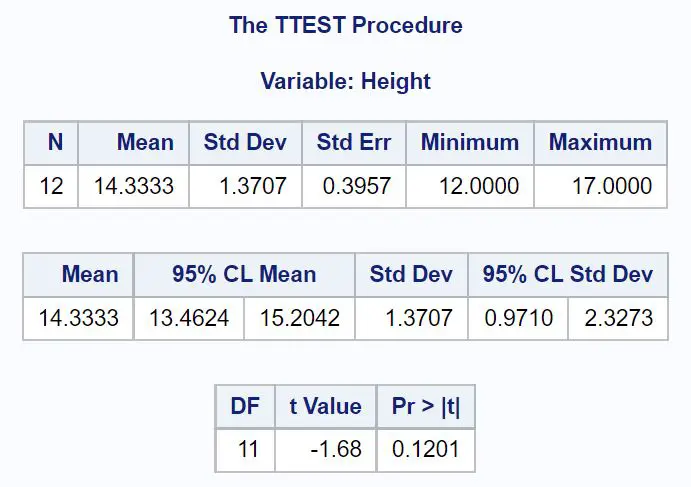
Le premier tableau affiche des statistiques descriptives pour notre échantillon, notamment :
- N (observations totales) : 12
- Moyenne (moyenne de l’échantillon) : 14,3333
- Std Dev (écart type de l’échantillon) : 1,3707
- Erreur standard (erreur standard, calculée comme s/√ n ) : 0,3957
- Minimum (la valeur minimale): 12
- Maximum (la valeur maximale) 17
Le deuxième tableau affiche l’ intervalle de confiance à 95 % pour la vraie moyenne de la population :
- IC à 95 % pour μ : [13,4624, 15,2042]
Le troisième tableau affiche la statistique du test t et la valeur p correspondante :
- statistique du test t : -1,68
- Valeur p : 0,1201
Remarque : La statistique du test t a été calculée comme suit :
- t statistique de test = ( x – μ) / (s/√ n )
- statistique du test t = (14,3333-15) / (1,3707/√ 12 )
- statistique du test t = -1,68
Rappelons que le test t sur un échantillon utilise les hypothèses nulles et alternatives suivantes :
- H 0 : μ = 15 pouces
- H A : μ ≠ 15 pouces
Puisque la valeur p ( .1201 ) n’est pas inférieure à 0.05, nous ne parvenons pas à rejeter l’hypothèse nulle.
Cela signifie que nous n’avons pas suffisamment de preuves pour affirmer que la hauteur moyenne de certaines espèces de plantes est différente de 15 pouces.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tests statistiques courants dans SAS :
Comment effectuer un test de classement signé Wilcoxon dans SAS
Comment effectuer une ANOVA unidirectionnelle dans SAS
