Comment utiliser le CDF normal dans R (avec exemples)
Vous pouvez utiliser les méthodes suivantes pour travailler avec le CDF (fonction de distribution cumulative) normal dans R :
Méthode 1 : calculer les probabilités CDF normales
#calculate probability that random value is less than 1.96 in normal CDF pnorm(1.96) #calculate probability that random value is greater than 1.96 in normal CDF pnorm(1.96, lower.tail=FALSE)
Méthode 2 : tracer le CDF normal
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #plot normal CDF plot(x, prob, type="l")
Les exemples suivants montrent comment utiliser ces méthodes dans la pratique.
Exemple 1 : Calculer les probabilités CDF normales
Le code suivant montre comment calculer la probabilité qu’une variable aléatoire prenne une valeur inférieure à 1,96 dans une distribution normale standard :
#calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)
[1] 0.9750021
La probabilité qu’une variable aléatoire prenne une valeur inférieure à 1,96 dans une distribution normale standard est de 0,975 .
Nous pouvons également trouver la probabilité qu’une variable aléatoire prenne une valeur supérieure à 1,96 en utilisant l’argument lower.tail :
#calculate probability that random value is greater than 1.96 in normal CDF pnorm(1.96, lower.tail=FALSE) [1] 0.0249979
Et nous pouvons utiliser la syntaxe suivante pour trouver la probabilité qu’une variable aléatoire prenne une valeur comprise entre deux valeurs dans une distribution normale standard :
#calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)
[1] 0.9500042
La probabilité qu’une variable aléatoire prenne une valeur comprise entre -1,96 et 1,96 dans une distribution normale standard est de 0,95 .
Exemple 2 : tracer le CDF normal
Le code suivant montre comment tracer un CDF normal :
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #plot normal CDF plot(x, prob, type="l")
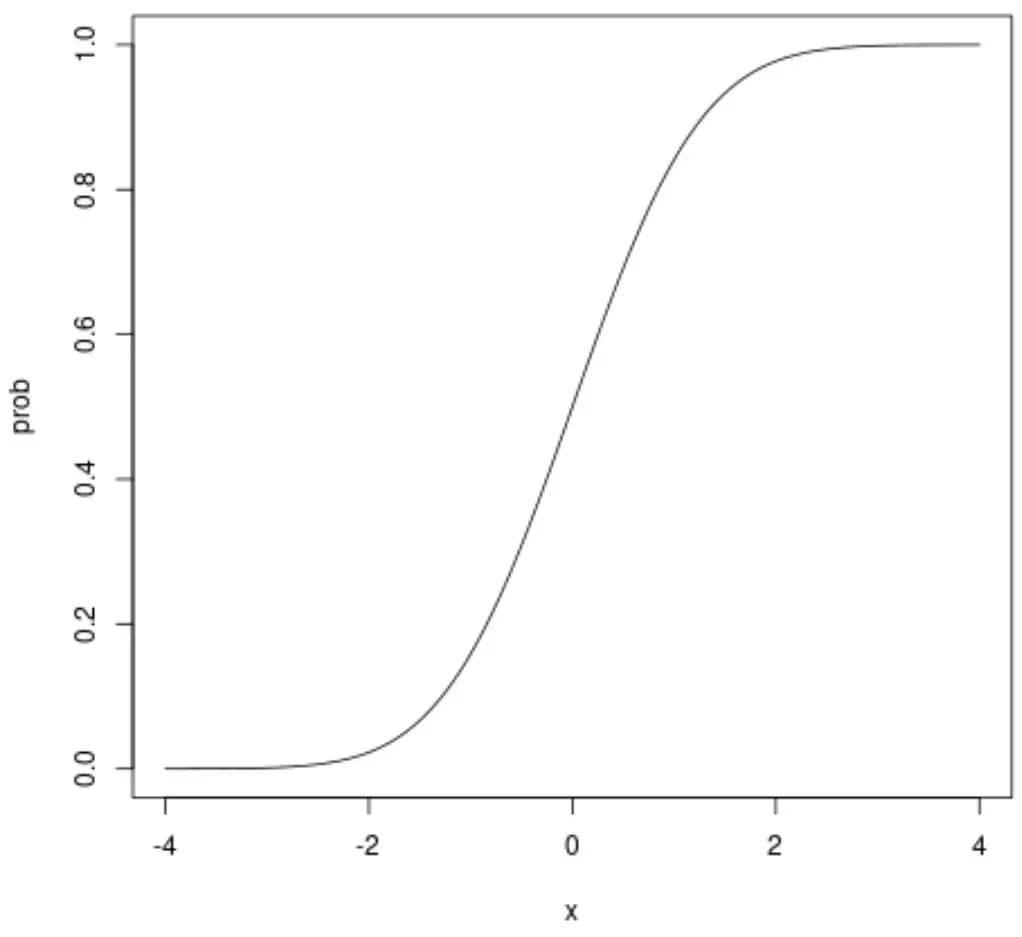
L’axe des x montre les valeurs d’une variable aléatoire qui suit une distribution normale standard et l’axe des y montre la probabilité qu’une variable aléatoire prenne une valeur inférieure à la valeur indiquée sur l’axe des x.
Par exemple, si nous regardons x = 1,96, nous verrons que la probabilité cumulée que x soit inférieur à 1,96 est d’environ 0,975 :
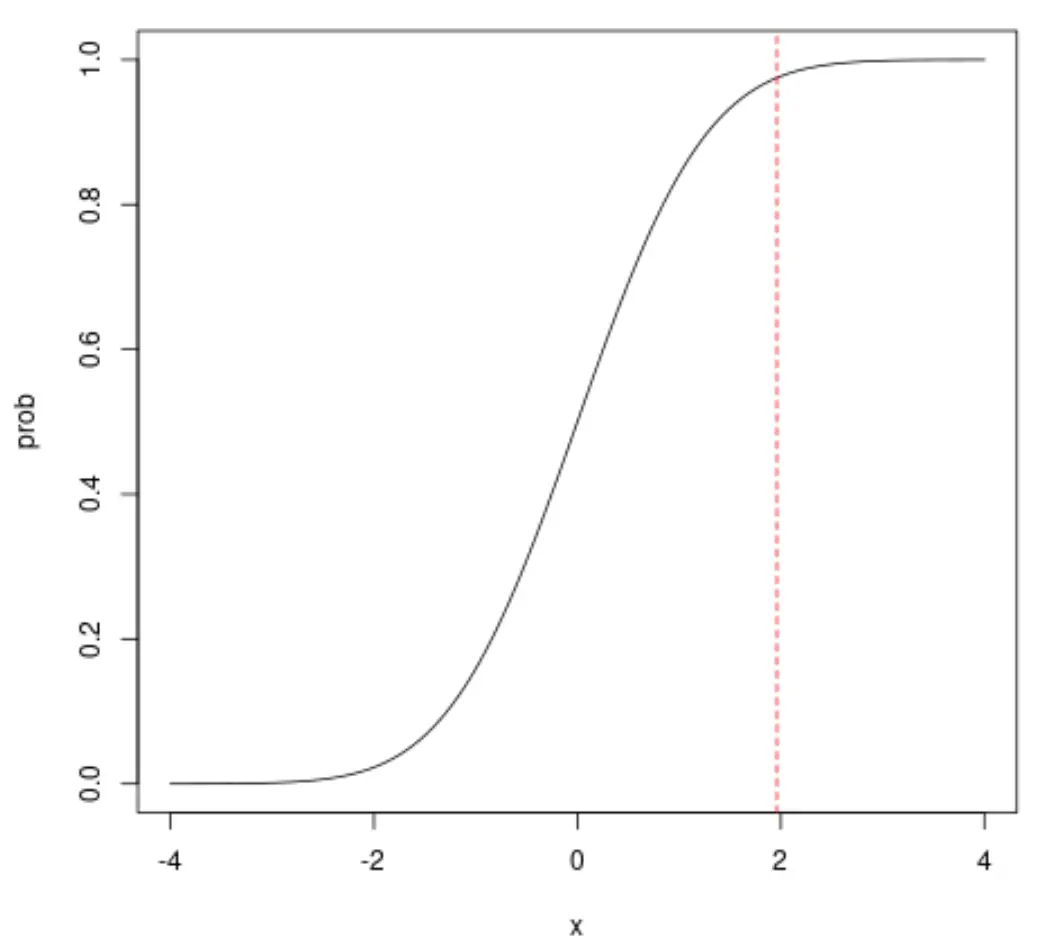
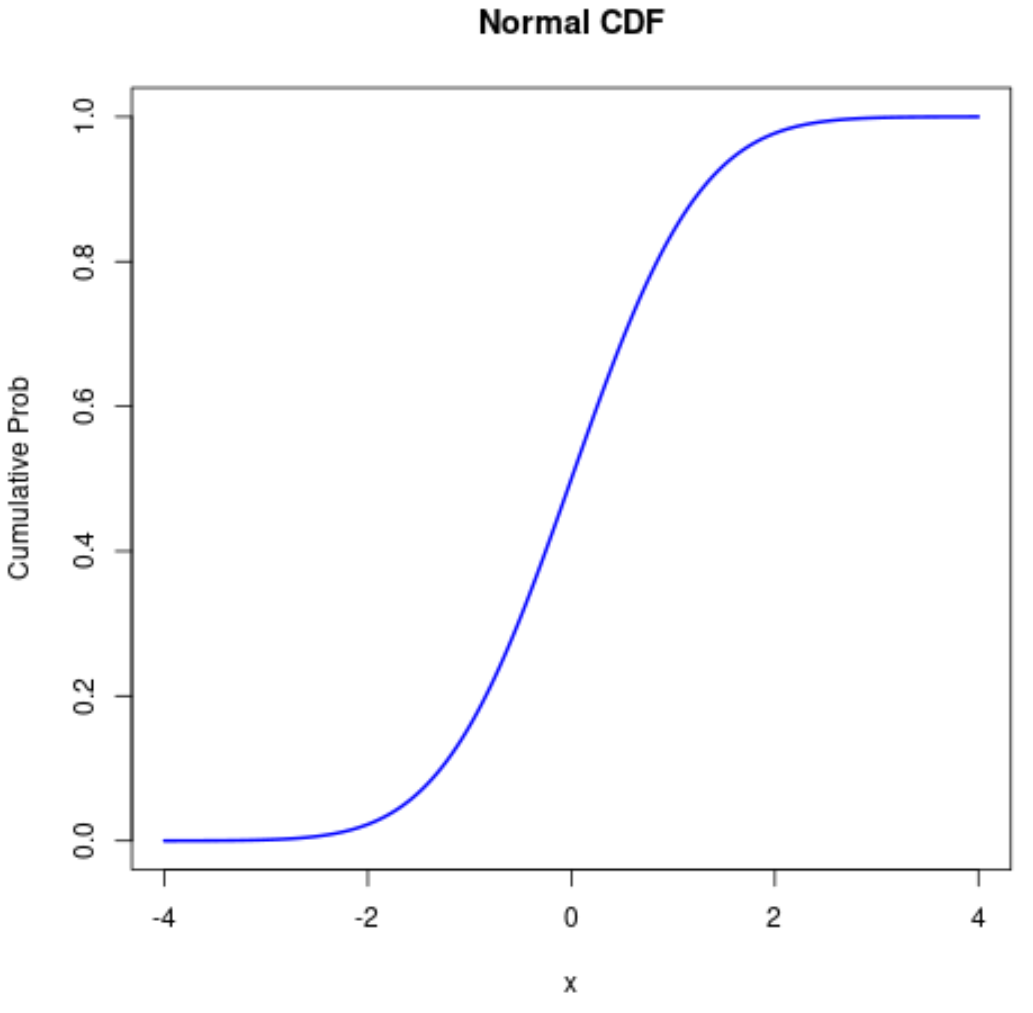
Notez que vous pouvez également modifier l’esthétique du tracé CDF normal :
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #plot normal CDF plot(x, prob, type='l', col='blue', lwd=2, main='Normal CDF', ylab='Cumulative Prob')
Connexe : Comment utiliser la fonction seq dans R
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres opérations courantes dans R :
Comment tracer une distribution normale dans R
Comment calculer les scores Z dans R
Un guide sur dnorm, pnorm, qnorm et rnorm dans R
