5 exemples de calcul de la valeur attendue dans la vie réelle

La valeur attendue est une valeur qui nous indique la moyenne attendue qu’une variable aléatoire prendra dans un nombre infini d’essais.

Nous utilisons la formule suivante pour calculer la valeur attendue d’un événement :

Valeur attendue = Σx * P(x)

où:

• x : valeur des données
• P(x) : Probabilité de valeur

Cette formule peut sembler un peu déroutante, mais elle aura plus de sens lorsque vous la verrez utilisée dans le contexte d’exemples réels.

Les exemples suivants montrent comment la valeur attendue est calculée dans cinq situations réelles différentes.

Exemple 1 : Investissements

La valeur attendue est souvent utilisée par les sociétés commerciales pour déterminer le profit ou la perte attendu d’un investissement.

Par exemple, supposons qu’un investissement particulier puisse générer un rendement annuel de 5 % avec une probabilité de 0,95, mais qu’il puisse également générer un rendement annuel de -20 % avec une probabilité de 0,05.

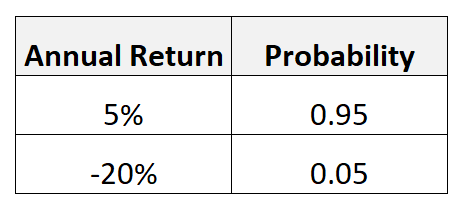
Nous calculerions la valeur attendue de cet investissement comme suit :

• Valeur attendue = 5%*.95 + (-20%)*.05 = 3.75%

Cet investissement particulier a une valeur attendue positive.

Cela signifie que si nous investissions dans cet investissement particulier un nombre infini de fois, nous nous attendrions à un rendement annuel moyen à long terme de 3,75 %.

Exemple 2 : Météo

La valeur attendue est souvent utilisée par les entreprises agricoles pour déterminer la quantité de pluie attendue qui tombera au cours d’une saison donnée.

Par exemple, supposons qu’il y ait 20 % de chances d’avoir 1 pouce de pluie, 70 % de chances d’avoir 2 pouces de pluie et 10 % de chances d’avoir 3 pouces de pluie.

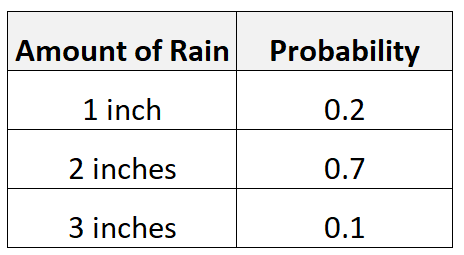
Nous calculerions la valeur attendue de la quantité de pluie comme suit :

• Valeur attendue = 0,2*1 + 0,7*2 + 0,1*3 = 1,9 pouces

Exemple 3 : Jeux de hasard

La valeur attendue est souvent utilisée par les joueurs pour déterminer combien ils pourraient potentiellement gagner à un jeu donné.

Par exemple, supposons que dans un certain jeu, il y ait 5 % de chances de gagner 100 $, 50 % de chances de gagner 0 $ et 45 % de chances de perdre 20 $.

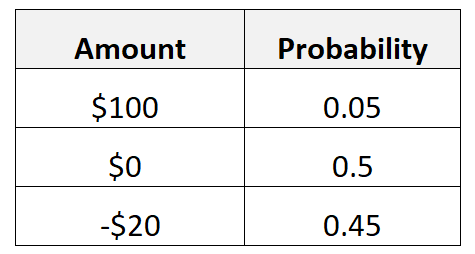
Nous calculerions la valeur attendue des gains comme suit :

• Valeur attendue = 0,05*100$ + 0,5*0$ + 0,45*(-20$) = -4$

Cela signifie que si nous jouions à ce jeu un nombre infini de fois, nous nous attendrions à perdre 4 $ à chaque fois que nous jouons, en moyenne.

Exemple 4 : Entreprise

La valeur attendue est souvent utilisée par les entreprises pour calculer le retour attendu sur les dépenses publicitaires.

Par exemple, supposons que pour une publicité particulière, il y ait 10 % de chances de recevoir un retour de 5 $, 30 % de chances de recevoir un retour de 2 $ et 60 % de chances de recevoir un retour de -8 $.

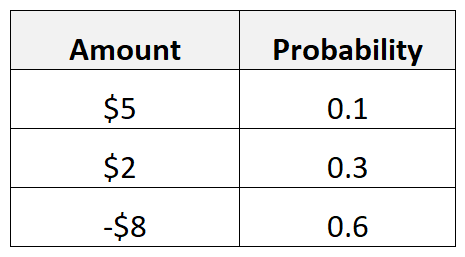
Nous calculerions la valeur attendue de la publicité comme suit :

• Valeur attendue = 0,1*5$ + 0,3*2$ + 0,6*(-8$) = -3,70$

Cette publicité particulière a une valeur attendue négative.

Cela signifie que si l’entreprise utilisait cette publicité particulière un nombre infini de fois, elle s’attendrait à perdre en moyenne 3,70 $ à chaque fois.

Exemple 5 : Entreprenariat

La valeur attendue est souvent utilisée par les individus pour décider s’ils doivent ou non se lancer dans l’entrepreneuriat.

Par exemple, supposons qu’un individu pense que s’il quitte son emploi et travaille à son compte, il a 60 % de chances de gagner 20 000 $ au cours de sa première année, 30 % de chances de gagner 60 000 $ et 10 % de chances de gagner 20 000 $. 0 $.

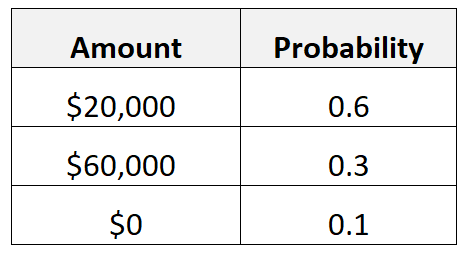
Nous calculerions la valeur attendue de leurs revenus au cours de la première année d’entrepreneuriat comme suit :

• Valeur attendue = 0,6*20 000 $ + 0,3*60 000 $ + 0,1*0 $ = 30 000 $

Selon que cette somme d’argent est suffisante ou non, l’individu pourra alors choisir de conserver son emploi actuel ou de le quitter.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la valeur attendue :

Comment calculer la valeur attendue dans Excel
Comment calculer la valeur attendue dans R (avec des exemples)
Valeur attendue par rapport à la moyenne : quelle est la différence ?