Comment utiliser la distribution t en Python
La distribution t est une distribution de probabilité similaire à la distribution normale , sauf qu’elle a des « queues » plus lourdes que la distribution normale.
Autrement dit, plus de valeurs dans la distribution sont situées aux extrémités que dans le centre par rapport à la distribution normale :
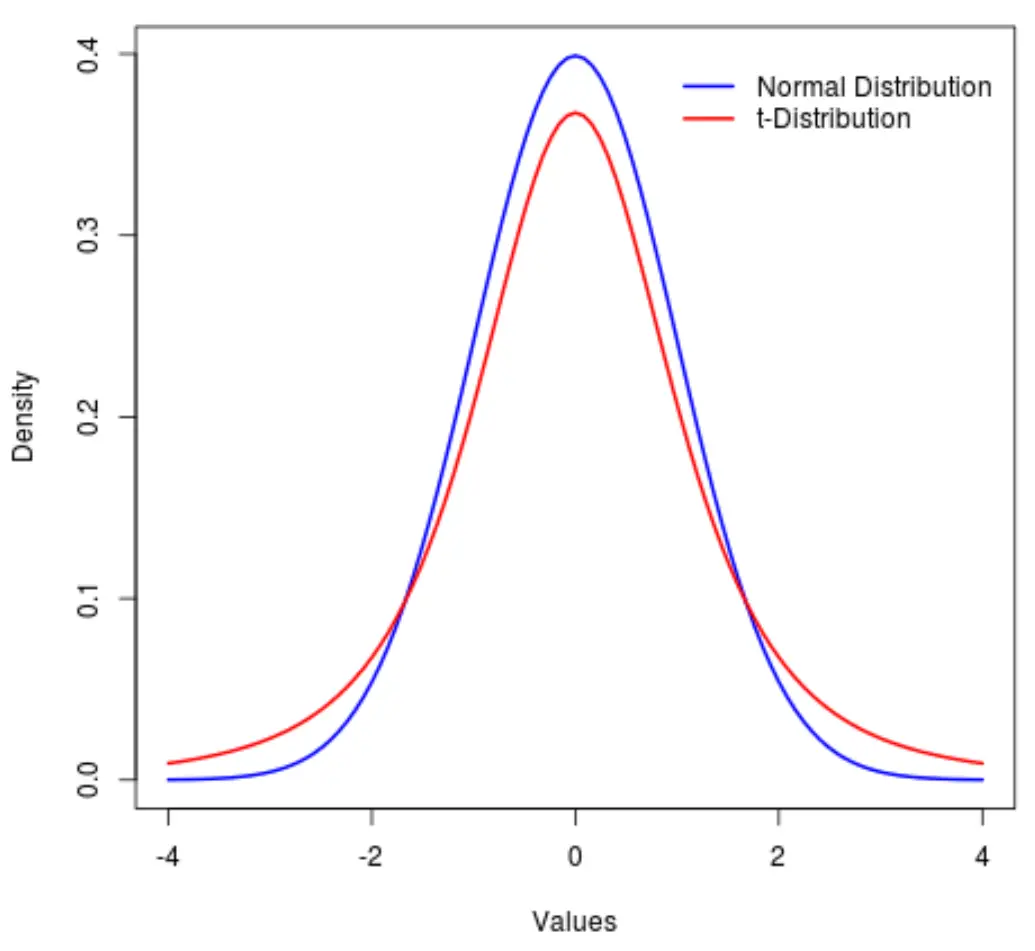
Ce tutoriel explique comment utiliser la distribution t en Python.
Comment générer à la distribution
Vous pouvez utiliser la fonction t.rvs(df, size) pour générer des valeurs aléatoires à partir d’une distribution avec des degrés de liberté et une taille d’échantillon spécifiques :
from scipy.stats import t #generate random values from t distribution with df=6 and sample size=10 t.rvs(df=6, size=10) array([-3.95799716, -0.01099963, -0.55953846, -1.53420055, -1.41775611, -0.45384974, -0.2767931 , -0.40177789, -0.3602592 , 0.38262431])
Le résultat est un tableau de 10 valeurs qui se suivent selon une distribution avec 6 degrés de liberté.
Comment calculer les valeurs P à l’aide de la distribution t
Nous pouvons utiliser la fonction t.cdf(x, df, loc=0, scale=1) pour trouver la valeur p associée à une statistique de test t.
Exemple 1 : Trouver une valeur P unilatérale
Supposons que nous effectuions un test d’hypothèse unilatéral et que nous obtenions une statistique de test de -1,5 et des degrés de liberté = 10 .
Nous pouvons utiliser la syntaxe suivante pour calculer la valeur p qui correspond à cette statistique de test :
from scipy.stats import t #calculate p-value t.cdf(x=-1.5, df=10) 0.08225366322272008
La valeur p unilatérale qui correspond à la statistique de test de -1,5 avec 10 degrés de liberté est de 0,0822 .
Exemple 2 : Trouver une valeur P bilatérale
Supposons que nous effectuions un test d’hypothèse bilatéral et que nous obtenions une statistique de test de 2,14 et des degrés de liberté = 20 .
Nous pouvons utiliser la syntaxe suivante pour calculer la valeur p qui correspond à cette statistique de test :
from scipy.stats import t #calculate p-value (1 - t.cdf(x=2.14, df=20)) * 2 0.04486555082549959
La valeur p bilatérale qui correspond à la statistique de test de 2,14 avec 20 degrés de liberté est de 0,0448 .
Remarque : Vous pouvez vérifier ces réponses à l’aide du calculateur de distribution t inverse .
Comment tracer à la distribution
Vous pouvez utiliser la syntaxe suivante pour tracer une distribution avec des degrés de liberté spécifiques :
from scipy.stats import t import matplotlib.pyplot as plt #generate t distribution with sample size 10000 x = t.rvs(df=12, size=10000) #create plot of t distribution plt.hist(x, density=True, edgecolor='black', bins=20)
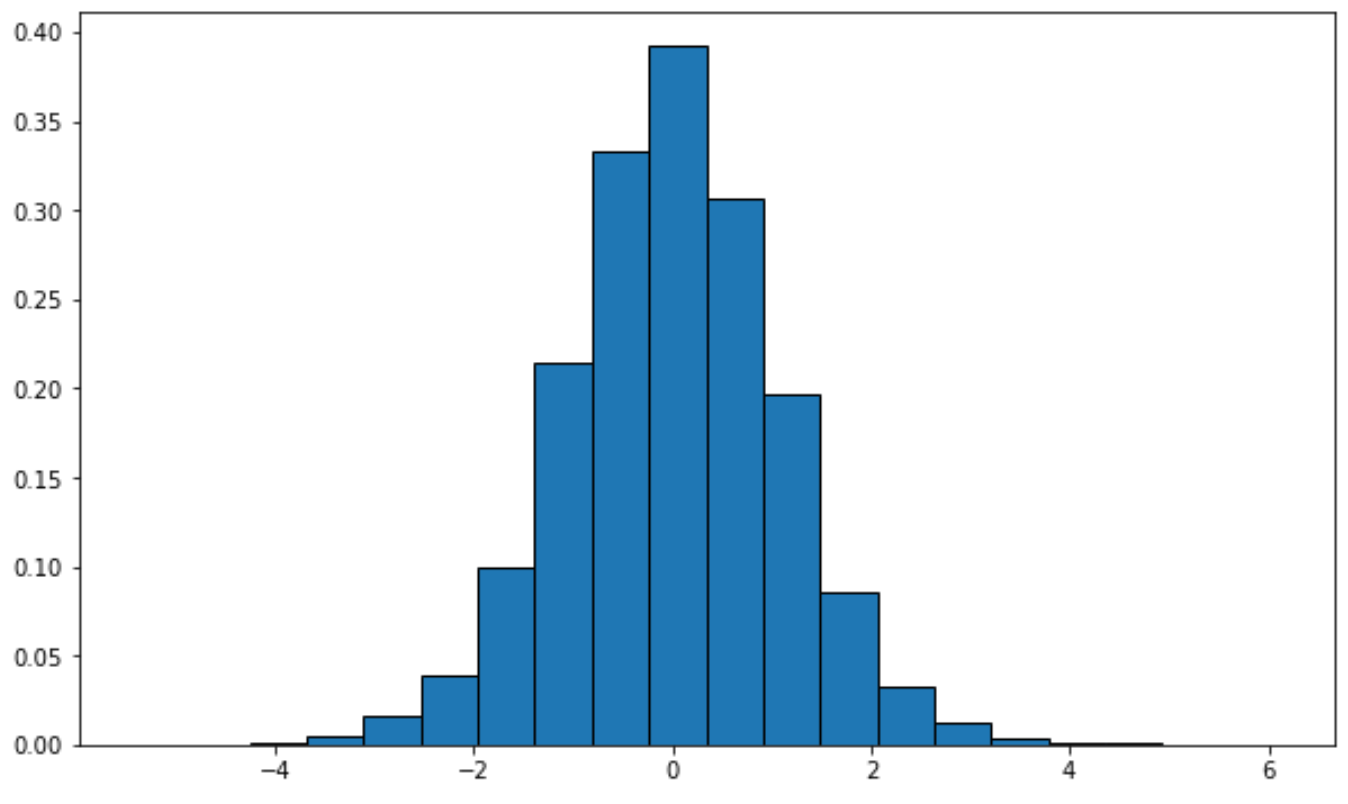
Alternativement, vous pouvez créer une courbe de densité à l’aide du package de visualisation seaborn :
import seaborn as sns #create density curve sns.kdeplot(x)
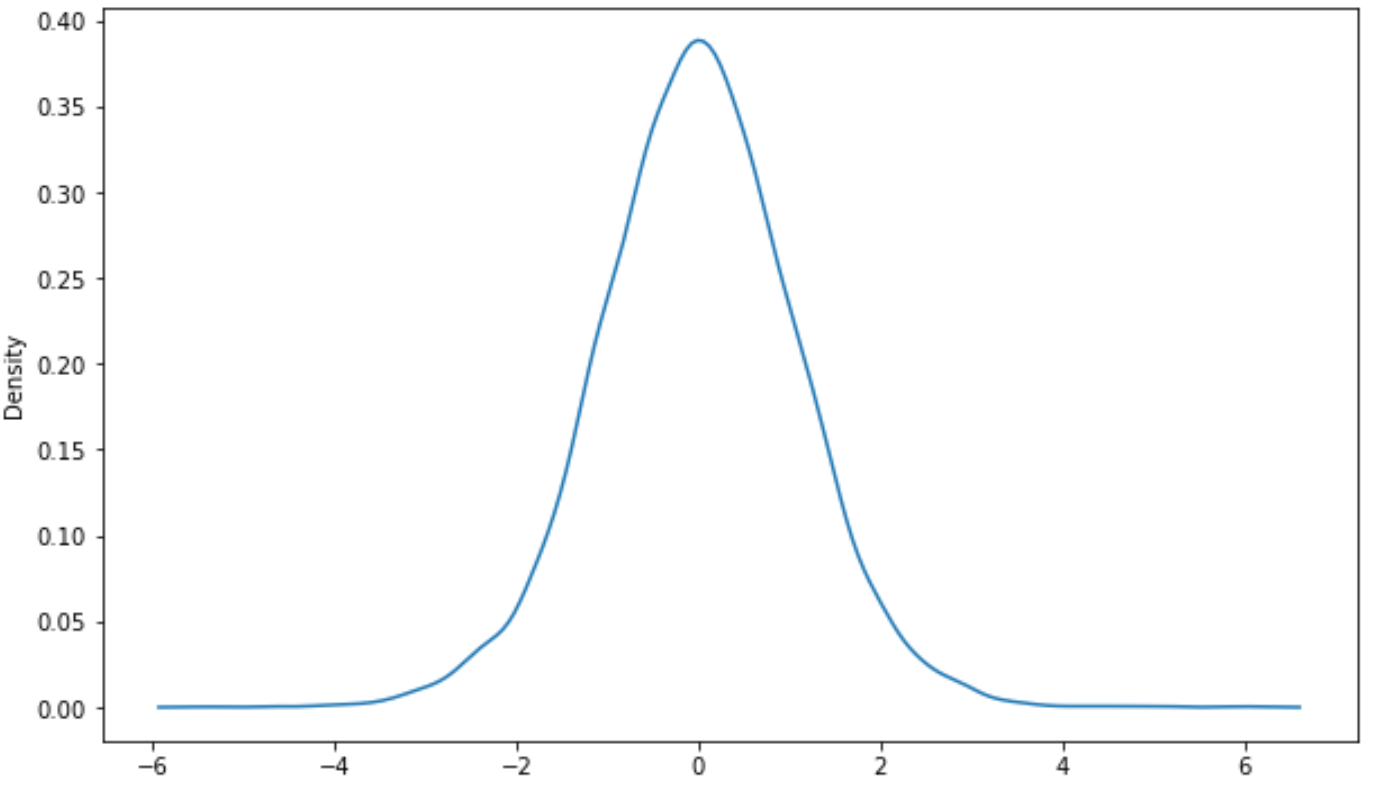
Ressources additionnelles
Les didacticiels suivants offrent des informations supplémentaires sur la distribution t :
Distribution normale vs distribution t : quelle est la différence ?
Calculateur de distribution t inverse
