Comprendre le test t dans la régression linéaire
La régression linéaire est utilisée pour quantifier la relation entre une variable prédictive et une variable de réponse.
Chaque fois que nous effectuons une régression linéaire, nous voulons savoir s’il existe une relation statistiquement significative entre la variable prédictive et la variable de réponse.
Nous testons la signification en effectuant un test t pour la pente de régression. Nous utilisons l’hypothèse nulle et alternative suivante pour ce test t :
- H 0 : β 1 = 0 (la pente est égale à zéro)
- H A : β 1 ≠ 0 (la pente n’est pas égale à zéro)
Nous calculons ensuite la statistique du test comme suit :
t = b / SE b
où:
- b : estimation du coefficient
- SE b : erreur type de l’estimation du coefficient
Si la valeur p qui correspond à t est inférieure à un certain seuil (par exemple α = 0,05), alors nous rejetons l’hypothèse nulle et concluons qu’il existe une relation statistiquement significative entre la variable prédictive et la variable réponse.
L’exemple suivant montre comment effectuer un test t pour un modèle de régression linéaire dans la pratique.
Exemple : exécution d’un test t pour la régression linéaire
Supposons qu’un professeur souhaite analyser la relation entre les heures étudiées et les notes obtenues aux examens pour 40 de ses étudiants.
Il effectue une régression linéaire simple en utilisant les heures étudiées comme variable prédictive et les résultats d’examen reçus comme variable de réponse.
Le tableau suivant montre les résultats du modèle de régression :
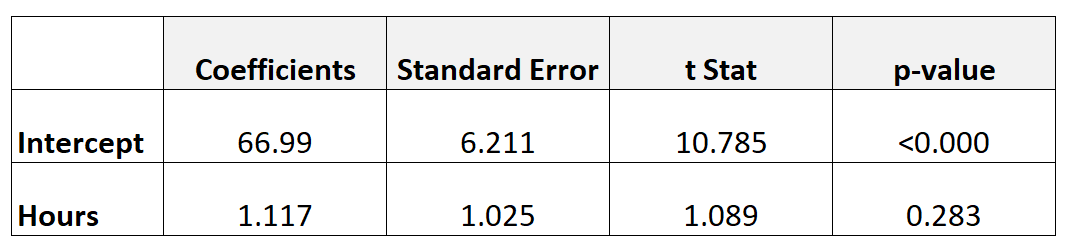
Pour déterminer si les heures étudiées ont une relation statistiquement significative avec la note de l’examen final, nous pouvons effectuer un test t.
Nous utilisons l’hypothèse nulle et alternative suivante pour ce test t :
- H 0 : β 1 = 0 (la pente des heures étudiées est égale à zéro)
- H A : β 1 ≠ 0 (la pente des heures étudiées n’est pas égale à zéro)
Nous calculons ensuite la statistique du test comme suit :
- t = b / SE b
- t = 1,117 / 1,025
- t = 1,089
La valeur p qui correspond à t = 1,089 avec df = n-2 = 40 – 2 = 38 est 0,283 .
Notez que nous pouvons également utiliser le calculateur de score T vers valeur P pour calculer cette valeur p :

Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.
Cela signifie que les heures étudiées n’ont pas de relation statistiquement significative entre les résultats de l’examen final.
Ressources additionnelles
Les didacticiels suivants offrent des informations supplémentaires sur la régression linéaire :
Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
Comment interpréter les coefficients de régression
Comment interpréter le test F de signification globale en régression
