MAE vs RMSE : quelle métrique devriez-vous utiliser ?

Les modèles de régression sont utilisés pour quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Chaque fois que nous ajustons un modèle de régression, nous voulons comprendre dans quelle mesure le modèle est capable d’utiliser les valeurs des variables prédictives pour prédire la valeur de la variable de réponse.

Deux mesures que nous utilisons souvent pour quantifier dans quelle mesure un modèle s’adapte à un ensemble de données sont l’erreur absolue moyenne (MAE) et l’erreur quadratique moyenne (RMSE), qui sont calculées comme suit :

MAE : Une métrique qui nous indique la différence absolue moyenne entre les valeurs prédites et les valeurs réelles dans un ensemble de données. Plus le MAE est faible, mieux un modèle s’adapte à un ensemble de données.

MAE = 1/n * Σ|y _je – ŷ _je |

où:

• Σ est un symbole qui signifie « somme »
• y _i est la valeur observée pour la ^ième observation
• ŷ _i est la valeur prédite pour la i ^ème observation
• n est la taille de l’échantillon

RMSE : Une métrique qui nous indique la racine carrée de la différence quadratique moyenne entre les valeurs prédites et les valeurs réelles dans un ensemble de données. Plus le RMSE est bas, mieux un modèle s’adapte à un ensemble de données.

Il est calculé comme suit :

RMSE = √ Σ(y _je – ŷ _je ) ² / n

où:

• Σ est un symbole qui signifie « somme »
• ŷ _i est la valeur prédite pour la i ^ème observation
• y _i est la valeur observée pour la ^ième observation
• n est la taille de l’échantillon

Exemple : Calcul du RMSE et du MAE

Supposons que nous utilisions un modèle de régression pour prédire le nombre de points que 10 joueurs marqueront dans un match de basket-ball.

Le tableau suivant montre les points prédits par le modèle par rapport aux points réels marqués par les joueurs :

À l’aide du calculateur MAE , nous pouvons calculer que le MAE est de 3,2.

Cela nous indique que la différence absolue moyenne entre les valeurs prédites par le modèle et les valeurs réelles est de 3,2.

À l’aide du calculateur RMSE , nous pouvons calculer que le RMSE est égal à 4 .

Cela nous indique que la racine carrée des différences quadratiques moyennes entre les points marqués prédits et les points réellement marqués est de 4.

Notez que chaque métrique nous donne une idée de la différence typique entre la valeur prédite faite par le modèle et la valeur réelle dans l’ensemble de données, mais l’interprétation de chaque métrique est légèrement différente.

RMSE vs MAE : quelle métrique devriez-vous utiliser ?

Si vous souhaitez attribuer plus de poids aux observations qui sont plus éloignées de la moyenne (c’est-à-dire si un écart de 20 est plus de deux fois pire qu’un écart de 10), il est préférable d’utiliser le RMSE pour mesurer l’erreur, car le Le RMSE est plus sensible aux observations plus éloignées de la moyenne.

Cependant, si être « décalé » à 20 est deux fois plus grave qu’être « décalé » à 10 alors il est préférable d’utiliser le MAE.

Pour illustrer cela, supposons que nous ayons un joueur qui est clairement aberrant en termes de nombre de points marqués :

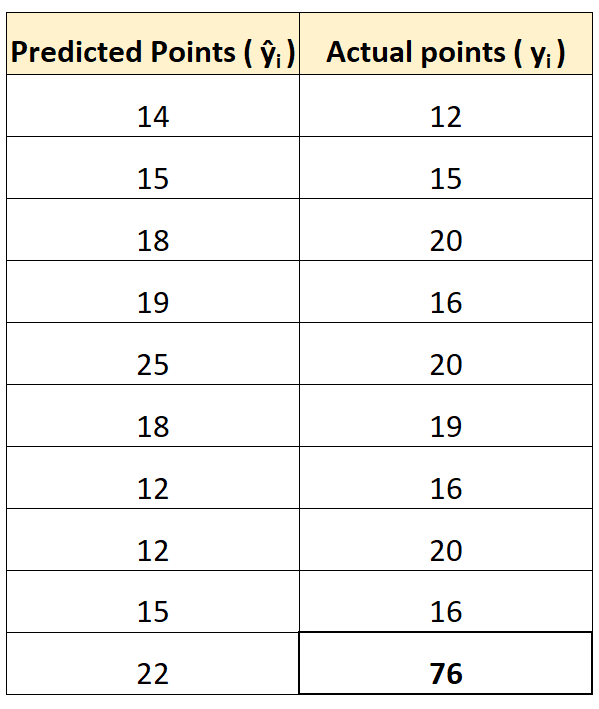
À l’aide des calculateurs en ligne mentionnés précédemment, nous pouvons calculer le MAE et le RMSE comme étant :

• MAE : 8
• RMSE : 16,4356

Notez que le RMSE augmente beaucoup plus que le MAE.

En effet, RMSE utilise des différences au carré dans sa formule et la différence au carré entre la valeur observée de 76 et la valeur prédite de 22 est assez grande. Cela entraîne une augmentation significative de la valeur du RMSE.

En pratique, nous adaptons généralement plusieurs modèles de régression à un ensemble de données et calculons une seule de ces métriques pour chaque modèle.

Par exemple, nous pourrions ajuster trois modèles de régression différents et calculer le RMSE pour chaque modèle. Nous sélectionnerions alors le modèle avec la valeur RMSE la plus basse comme « meilleur » modèle, car c’est celui qui fait les prédictions les plus proches des valeurs réelles de l’ensemble de données.

Dans les deux cas, assurez-vous simplement de calculer la même métrique pour chaque modèle. Par exemple, ne calculez pas le MAE pour un modèle et le RMSE pour un autre modèle, puis comparez ces deux mesures.

Ressources additionnelles

Les tutoriels suivants expliquent comment calculer le MAE à l’aide de différents logiciels statistiques :

Comment calculer l’erreur absolue moyenne dans Excel
Comment calculer l’erreur absolue moyenne dans R
Comment calculer l’erreur absolue moyenne en Python

Les tutoriels suivants expliquent comment calculer le RMSE à l’aide de différents logiciels statistiques :

Comment calculer l’erreur quadratique moyenne dans Excel
Comment calculer l’erreur quadratique moyenne dans R
Comment calculer l’erreur quadratique moyenne en Python