Comprendre l’erreur standard d’une pente de régression

L’ erreur type d’une pente de régression est un moyen de mesurer « l’incertitude » dans l’estimation d’une pente de régression.

Il est calculé comme suit :

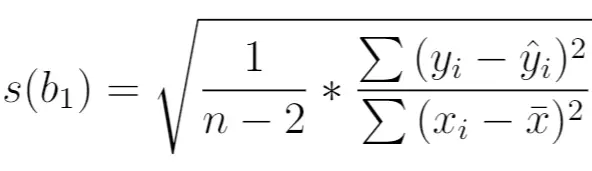
où:

• n : taille totale de l’échantillon
• y _i : valeur réelle de la variable de réponse
• ŷ _i : valeur prédite de la variable de réponse
• x _i : valeur réelle de la variable prédictive
• x̄ : valeur moyenne de la variable prédictive

Plus l’erreur type est petite, plus la variabilité autour de l’estimation du coefficient pour la pente de régression est faible.

L’erreur type de la pente de régression sera affichée dans une colonne « erreur type » dans la sortie de régression de la plupart des logiciels statistiques :

Les exemples suivants montrent comment interpréter l’erreur type d’une pente de régression dans deux scénarios différents.

Exemple 1 : Interprétation d’une petite erreur standard d’une pente de régression

Supposons qu’un professeur veuille comprendre la relation entre le nombre d’heures étudiées et la note obtenue à l’examen final des étudiants de sa classe.

Il collecte des données pour 25 étudiants et crée le nuage de points suivant :

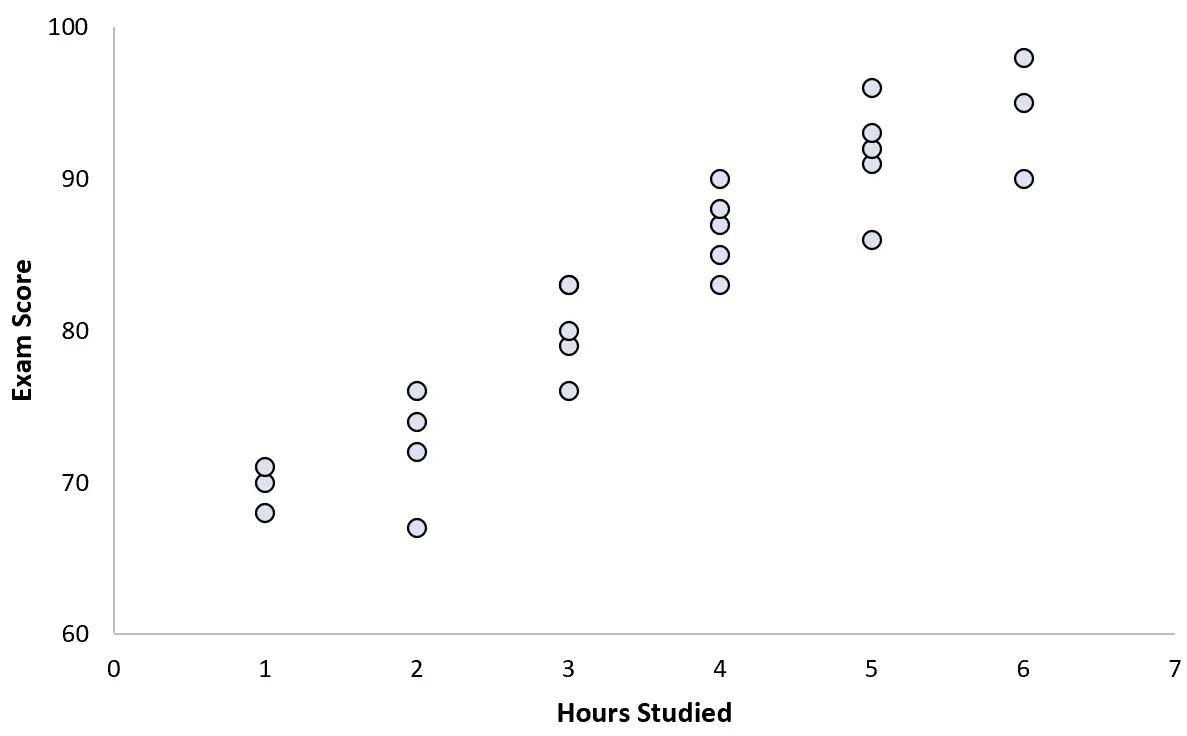
Il existe une association clairement positive entre les deux variables. À mesure que le nombre d’heures étudiées augmente, la note à l’examen augmente à un rythme assez prévisible.

Il a ensuite ajusté un modèle de régression linéaire simple en utilisant les heures étudiées comme variable prédictive et la note à l’examen final comme variable de réponse.

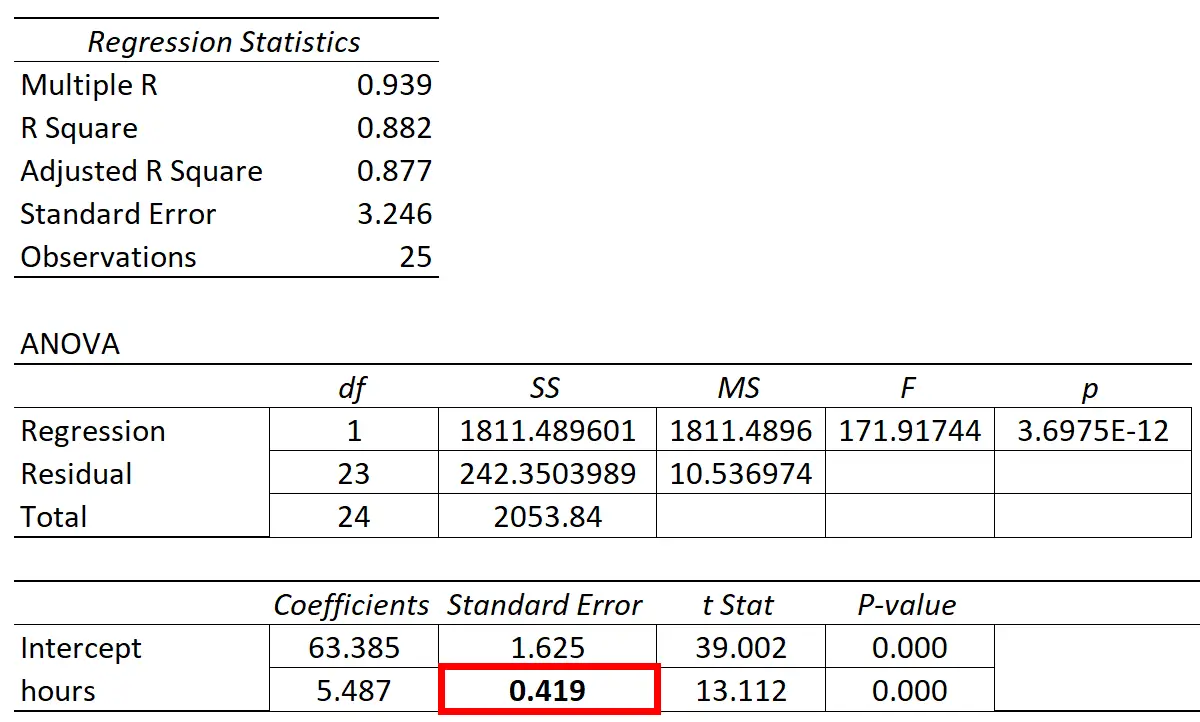
Le tableau suivant montre les résultats de la régression :

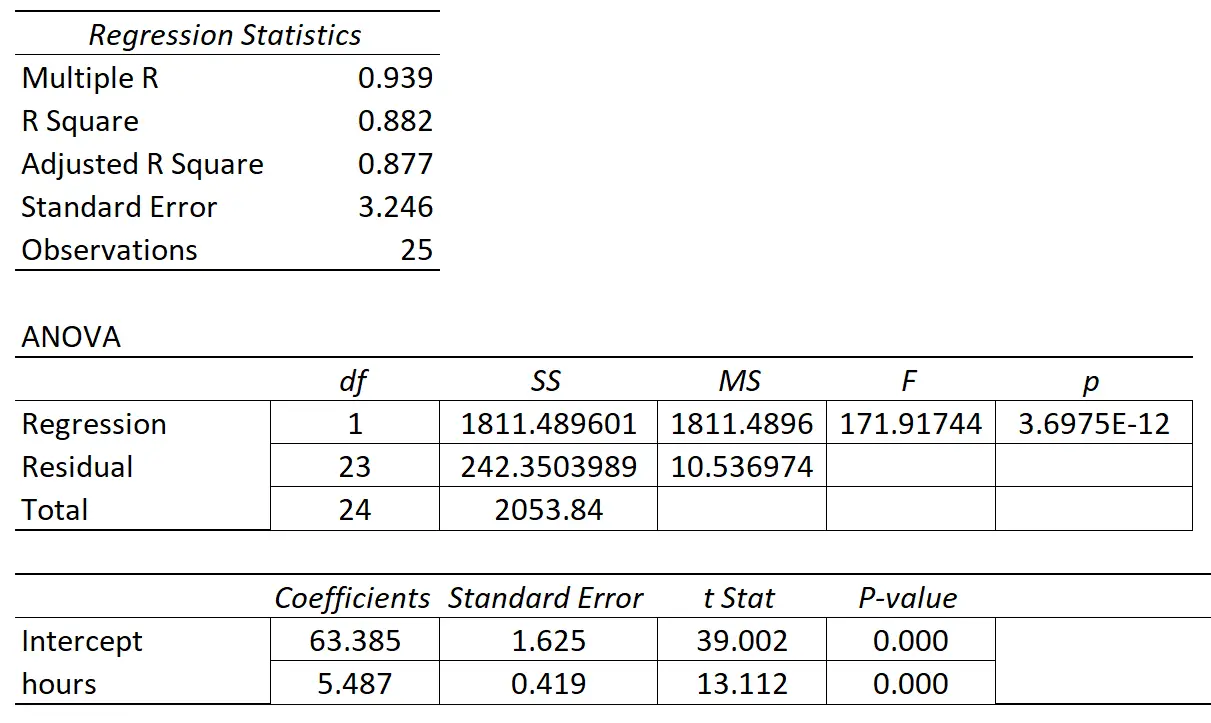
Le coefficient de la variable prédictive « heures d’études » est de 5,487. Cela nous indique que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de 5,487 de la note à l’examen.

L’erreur standard est de 0,419 , ce qui représente une mesure de la variabilité autour de cette estimation pour la pente de régression.

Nous pouvons utiliser cette valeur pour calculer la statistique t pour la variable prédictive « heures étudiées » :

• statistique t = estimation du coefficient / erreur standard
• statistique t = 5,487 / 0,419
• statistique t = 13,112

La valeur p qui correspond à cette statistique de test est de 0,000, ce qui indique que les « heures étudiées » ont une relation statistiquement significative avec la note finale de l’examen.

Étant donné que l’erreur type de la pente de régression était faible par rapport à l’estimation du coefficient de la pente de régression, la variable prédictive était statistiquement significative.

Exemple 2 : Interprétation d’une grande erreur type d’une pente de régression

Supposons qu’un autre professeur souhaite comprendre la relation entre le nombre d’heures étudiées et la note obtenue à l’examen final des étudiants de sa classe.

Elle collecte des données pour 25 étudiants et crée le nuage de points suivant :

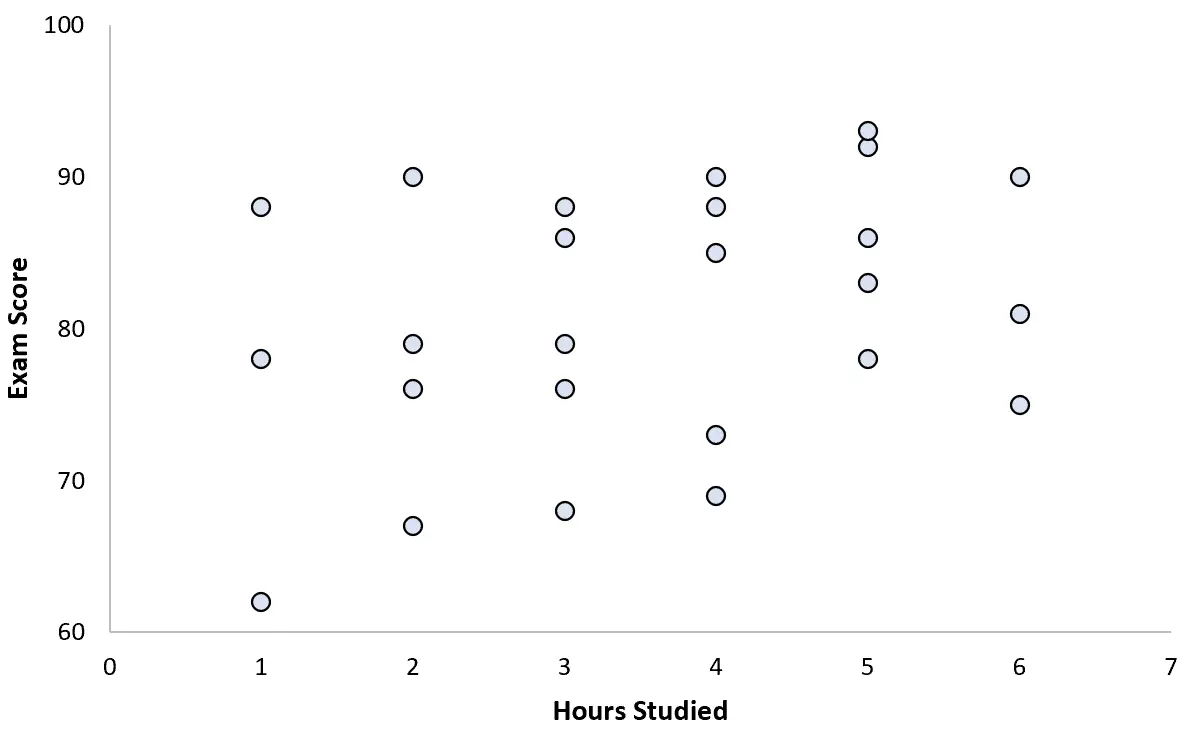
Il semble y avoir une légère association positive entre les deux variables. À mesure que le nombre d’heures d’étude augmente, la note à l’examen augmente généralement, mais pas à un rythme prévisible.

Supposons que le professeur ajuste ensuite un modèle de régression linéaire simple en utilisant les heures étudiées comme variable prédictive et la note à l’examen final comme variable de réponse.

Le tableau suivant montre les résultats de la régression :

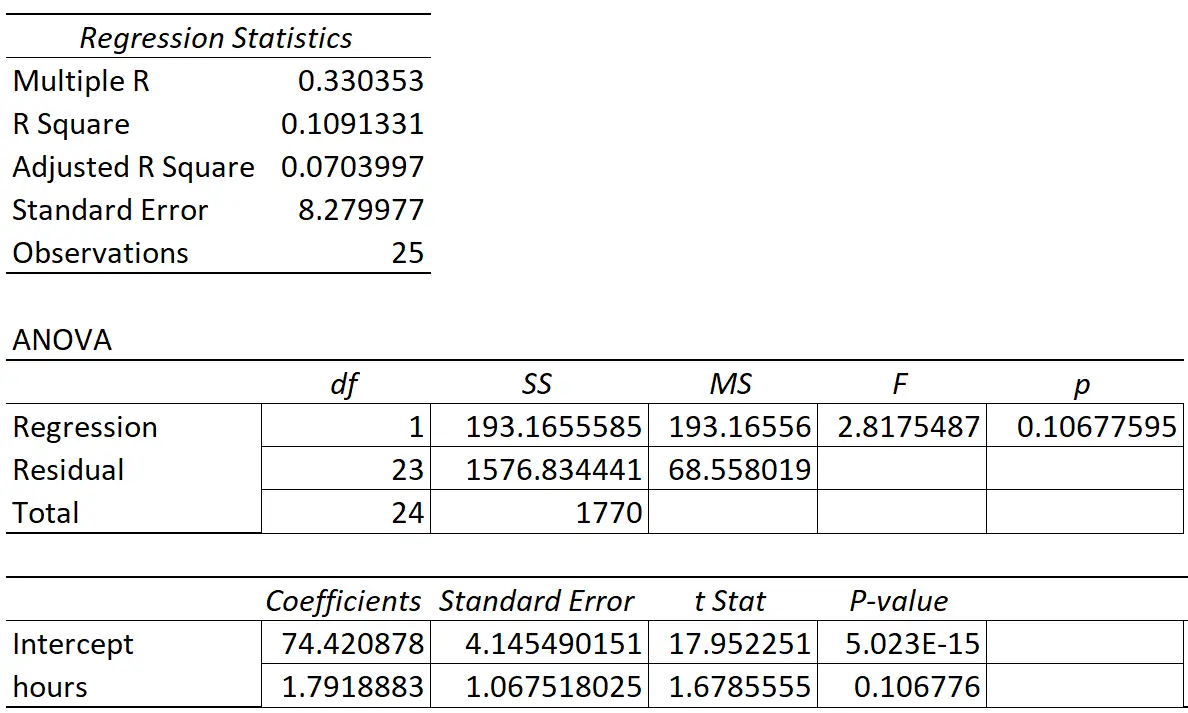
Le coefficient de la variable prédictive « heures d’études » est de 1,7919. Cela nous indique que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de 1,7919 de la note à l’examen.

L’erreur type est de 1,0675 , qui est une mesure de la variabilité autour de cette estimation pour la pente de régression.

Nous pouvons utiliser cette valeur pour calculer la statistique t pour la variable prédictive « heures étudiées » :

• statistique t = estimation du coefficient / erreur type
• statistique t = 1,7919 / 1,0675
• statistique t = 1,678

La valeur p qui correspond à cette statistique de test est de 0,107. Puisque cette valeur p n’est pas inférieure à 0,05, cela indique que les « heures étudiées » n’ont pas de relation statistiquement significative avec la note de l’examen final.

Étant donné que l’erreur type de la pente de régression était importante par rapport à l’estimation du coefficient de la pente de régression, la variable prédictive n’était pas statistiquement significative.

Ressources additionnelles

Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
Comment lire et interpréter un tableau de régression