Comment tester la normalité dans R (4 méthodes)

De nombreux tests statistiques supposent que les ensembles de données sont normalement distribués.

Il existe quatre manières courantes de vérifier cette hypothèse dans R :

1. (Méthode visuelle) Créez un histogramme.

• Si l’histogramme est à peu près en forme de « cloche », alors les données sont supposées être distribuées normalement.

2. (Méthode visuelle) Créez un tracé QQ.

• Si les points du tracé se situent à peu près le long d’une ligne diagonale droite, alors les données sont supposées être distribuées normalement.

3. (Test statistique formel) Effectuez un test Shapiro-Wilk.

• Si la valeur p du test est supérieure à α = 0,05, alors les données sont supposées être normalement distribuées.

4. (Test statistique formel) Effectuez un test de Kolmogorov-Smirnov.

• Si la valeur p du test est supérieure à α = 0,05, alors les données sont supposées être normalement distribuées.

Les exemples suivants montrent comment utiliser chacune de ces méthodes dans la pratique.

Méthode 1 : créer un histogramme

Le code suivant montre comment créer un histogramme pour un ensemble de données normalement distribué et non normalement distribué dans R :

#make this example reproducible
set.seed(0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
par(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col='steelblue', main='Normal')
hist(non_normal_data, col='steelblue', main='Non-normal')

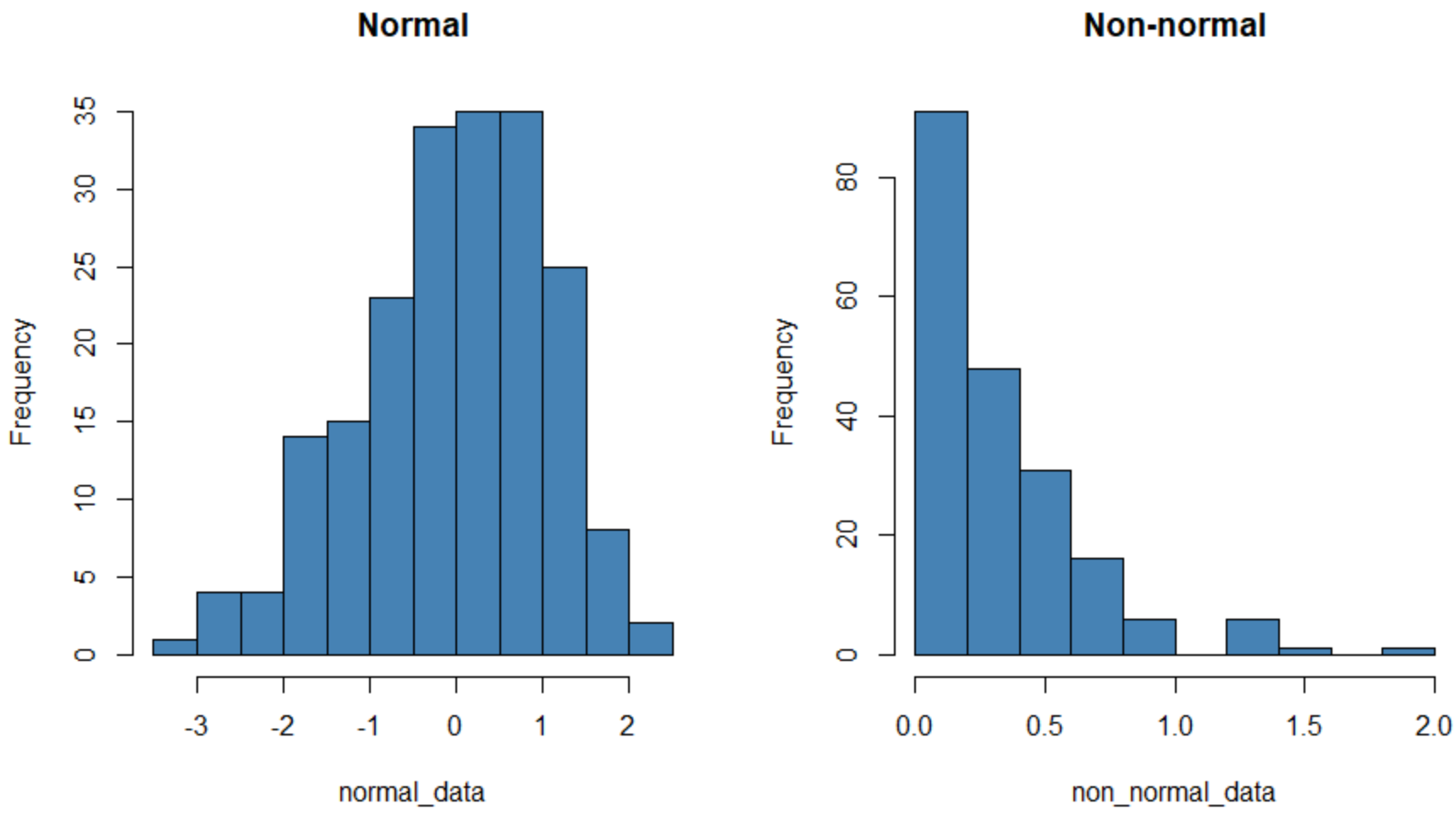
L’histogramme de gauche présente un ensemble de données qui est normalement distribué (à peu près en forme de « cloche ») et celui de droite présente un ensemble de données qui n’est pas normalement distribué.

Méthode 2 : créer un tracé QQ

Le code suivant montre comment créer un tracé QQ pour un ensemble de données normalement distribué et non normalement distribué dans R :

#make this example reproducible
set.seed(0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
par(mfrow=c(1,2)) 

#create Q-Q plot for both datasets
qqnorm(normal_data, main='Normal')
qqline(normal_data)

qqnorm(non_normal_data, main='Non-normal')
qqline(non_normal_data)

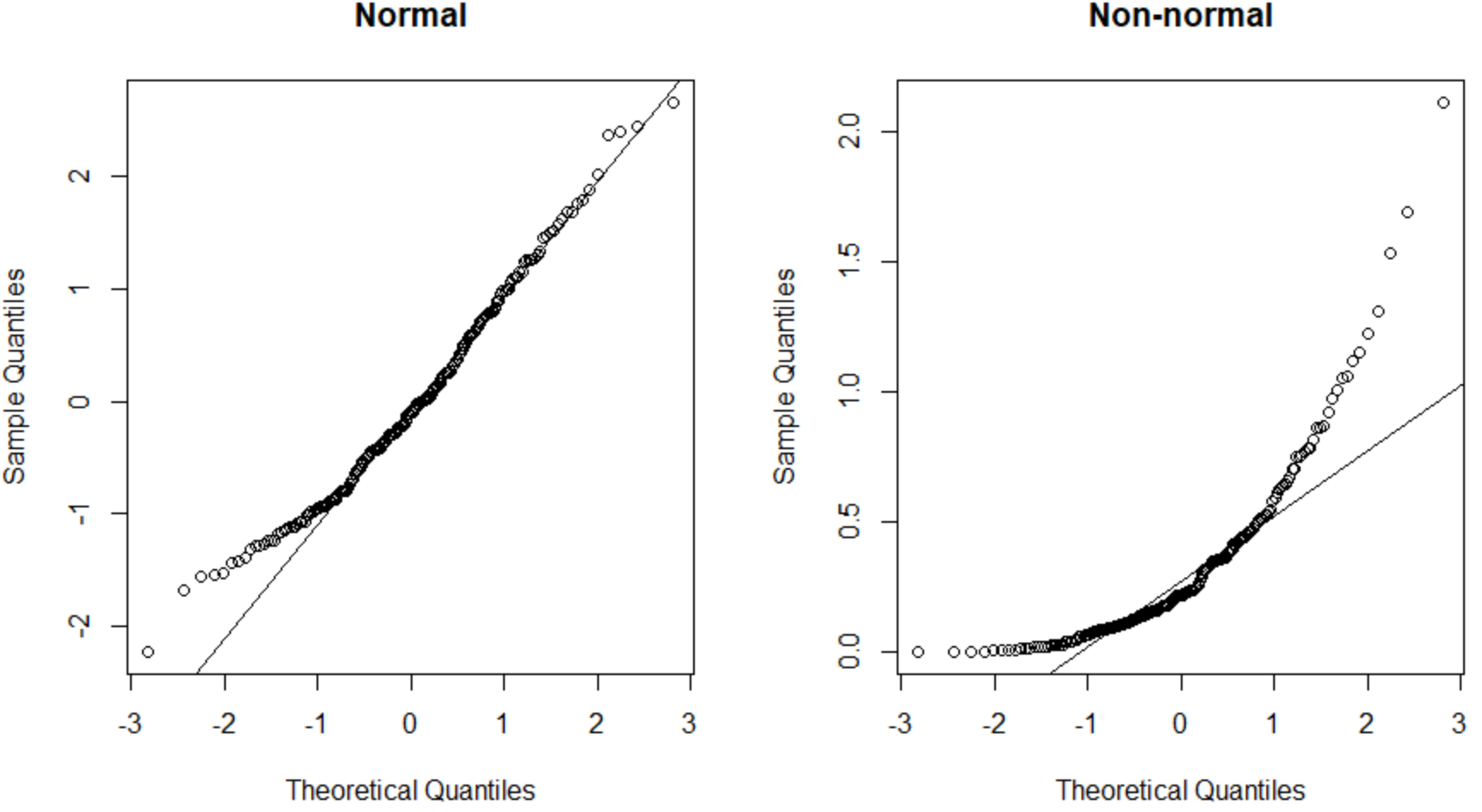
Le tracé QQ de gauche présente un ensemble de données qui est normalement distribué (les points tombent le long d’une ligne diagonale droite) et le tracé QQ de droite présente un ensemble de données qui n’est pas normalement distribué.

Méthode 3 : effectuer un test Shapiro-Wilk

Le code suivant montre comment effectuer un test Shapiro-Wilk sur un ensemble de données normalement distribué et non normalement distribué dans R :

#make this example reproducible
set.seed(0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro.test(normal_data)

	Shapiro-Wilk normality test

data:  normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro.test(non_normal_data)

	Shapiro-Wilk normality test

data:  non_normal_data
W = 0.84153, p-value = 1.698e-13

La valeur p du premier test n’est pas inférieure à 0,05, ce qui indique que les données sont normalement distribuées.

La valeur p du deuxième test est inférieure à 0,05, ce qui indique que les données ne sont pas normalement distribuées.

Méthode 4 : effectuer un test de Kolmogorov-Smirnov

Le code suivant montre comment effectuer un test de Kolmogorov-Smirnov sur un ensemble de données normalement distribué et non normalement distribué dans R :

#make this example reproducible
set.seed(0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks.test(normal_data, 'pnorm')

	One-sample Kolmogorov-Smirnov test

data:  normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks.test(non_normal_data, 'pnorm') 
	One-sample Kolmogorov-Smirnov test

data:  non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

La valeur p du premier test n’est pas inférieure à 0,05, ce qui indique que les données sont normalement distribuées.

La valeur p du deuxième test est inférieure à 0,05, ce qui indique que les données ne sont pas normalement distribuées.

Comment gérer les données non normales

Si un ensemble de données donné n’est pas normalement distribué, nous pouvons souvent effectuer l’une des transformations suivantes pour le rendre plus normalement distribué :

1. Transformation du journal : transformez les valeurs de x en log(x) .

2. Transformation racine carrée : Transformez les valeurs de x en √ x .

3. Transformation de racine cubique : transformez les valeurs de x en x ^1/3 .

En effectuant ces transformations, l’ensemble de données devient généralement distribué plus normalement.

Lisez ce tutoriel pour voir comment effectuer ces transformations dans R.

Ressources additionnelles

Comment créer des histogrammes dans R
Comment créer et interpréter un tracé QQ dans R
Comment effectuer un test Shapiro-Wilk dans R
Comment effectuer un test de Kolmogorov-Smirnov dans R