Comment transformer des données en Python (journal, racine carrée, racine cubique)
De nombreux tests statistiques supposent que les ensembles de données sont normalement distribués. Or, ce n’est souvent pas le cas dans la pratique.
Une façon de résoudre ce problème consiste à transformer la distribution des valeurs dans un ensemble de données à l’aide de l’une des trois transformations suivantes :
1. Transformation du journal : transformez la variable de réponse de y en log(y) .
2. Transformation racine carrée : Transformez la variable de réponse de y en √ y .
3. Transformation de racine cubique : transformez la variable de réponse de y en y 1/3 .
En effectuant ces transformations, l’ensemble de données devient généralement distribué plus normalement.
Les exemples suivants montrent comment effectuer ces transformations en Python.
Transformation de journal en Python
Le code suivant montre comment effectuer une transformation logarithmique sur une variable et créer des tracés côte à côte pour afficher la distribution d’origine et la distribution transformée en log des données :
import numpy as np import matplotlib.pyplot as plt #make this example reproducible np.random.seed(0) #create beta distributed random variable with 200 values data = np.random.beta(a=4, b=15, size=300) #create log-transformed data data_log = np.log(data) #define grid of plots fig, axs = plt.subplots(nrows=1, ncols=2) #create histograms axs[0].hist(data, edgecolor='black') axs[1].hist(data_log, edgecolor='black') #add title to each histogram axs[0].set_title('Original Data') axs[1].set_title('Log-Transformed Data')
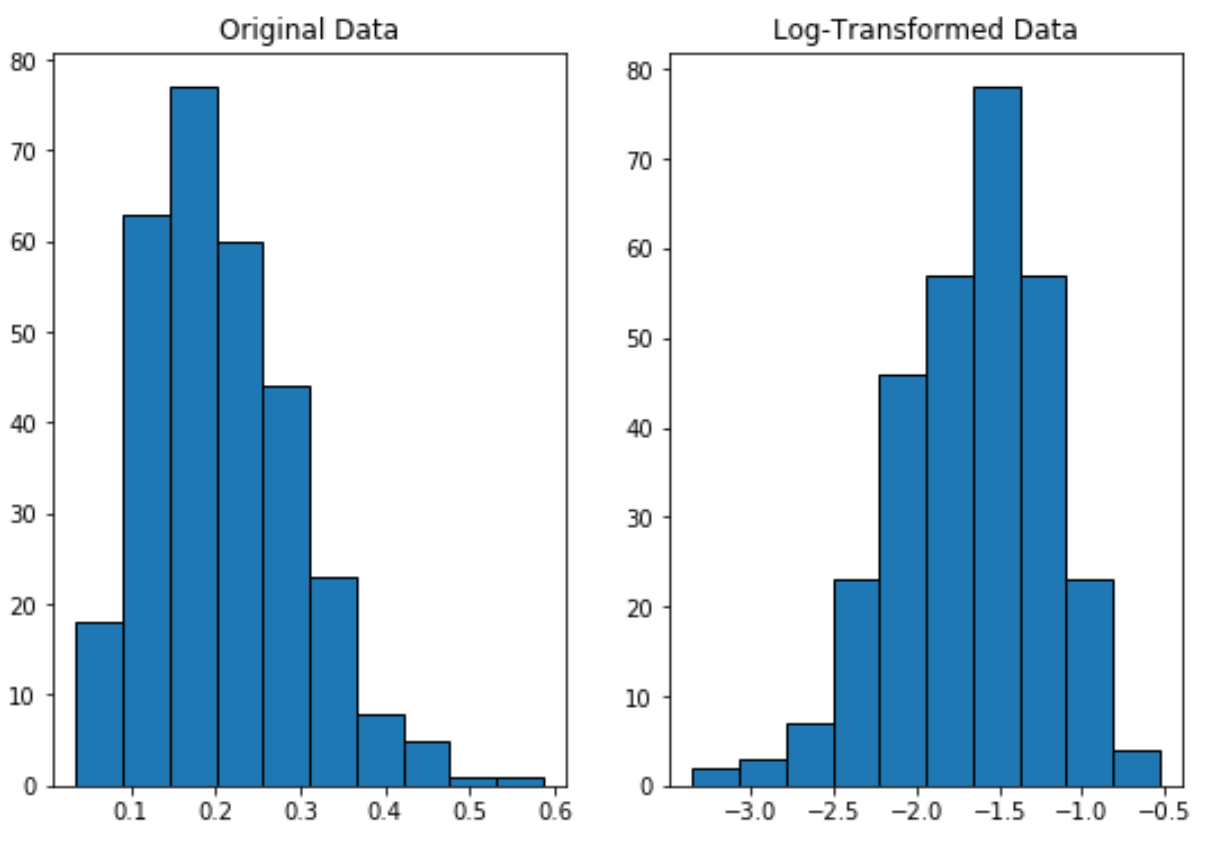
Remarquez comment la distribution transformée en log est distribuée plus normalement que la distribution d’origine.
Ce n’est toujours pas une « forme de cloche » parfaite mais elle est plus proche d’une distribution normale que de la distribution originale.
Transformation racine carrée en Python
Le code suivant montre comment effectuer une transformation racine carrée sur une variable et créer des tracés côte à côte pour afficher la distribution d’origine et la distribution transformée en racine carrée des données :
import numpy as np import matplotlib.pyplot as plt #make this example reproducible np.random.seed(0) #create beta distributed random variable with 200 values data = np.random.beta(a=1, b=5, size=300) #create log-transformed data data_log = np.sqrt(data) #define grid of plots fig, axs = plt.subplots(nrows=1, ncols=2) #create histograms axs[0].hist(data, edgecolor='black') axs[1].hist(data_log, edgecolor='black') #add title to each histogram axs[0].set_title('Original Data') axs[1].set_title('Square Root Transformed Data')
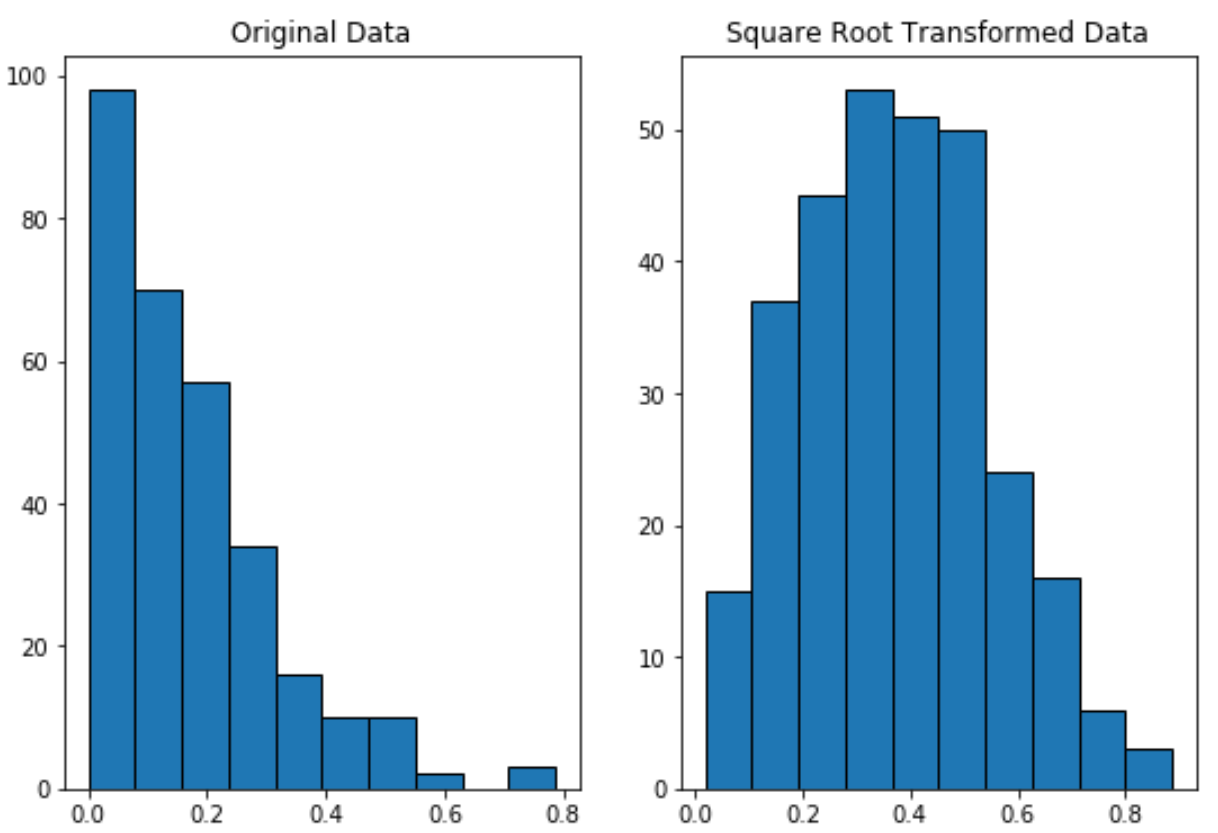
Remarquez comment les données transformées en racine carrée sont distribuées beaucoup plus normalement que les données d’origine.
Transformation de racine cubique en Python
Le code suivant montre comment effectuer une transformation de racine cubique sur une variable et créer des tracés côte à côte pour afficher la distribution d’origine et la distribution transformée de racine cubique des données :
import numpy as np import matplotlib.pyplot as plt #make this example reproducible np.random.seed(0) #create beta distributed random variable with 200 values data = np.random.beta(a=1, b=5, size=300) #create log-transformed data data_log = np.cbrt(data) #define grid of plots fig, axs = plt.subplots(nrows=1, ncols=2) #create histograms axs[0].hist(data, edgecolor='black') axs[1].hist(data_log, edgecolor='black') #add title to each histogram axs[0].set_title('Original Data') axs[1].set_title('Cube Root Transformed Data')
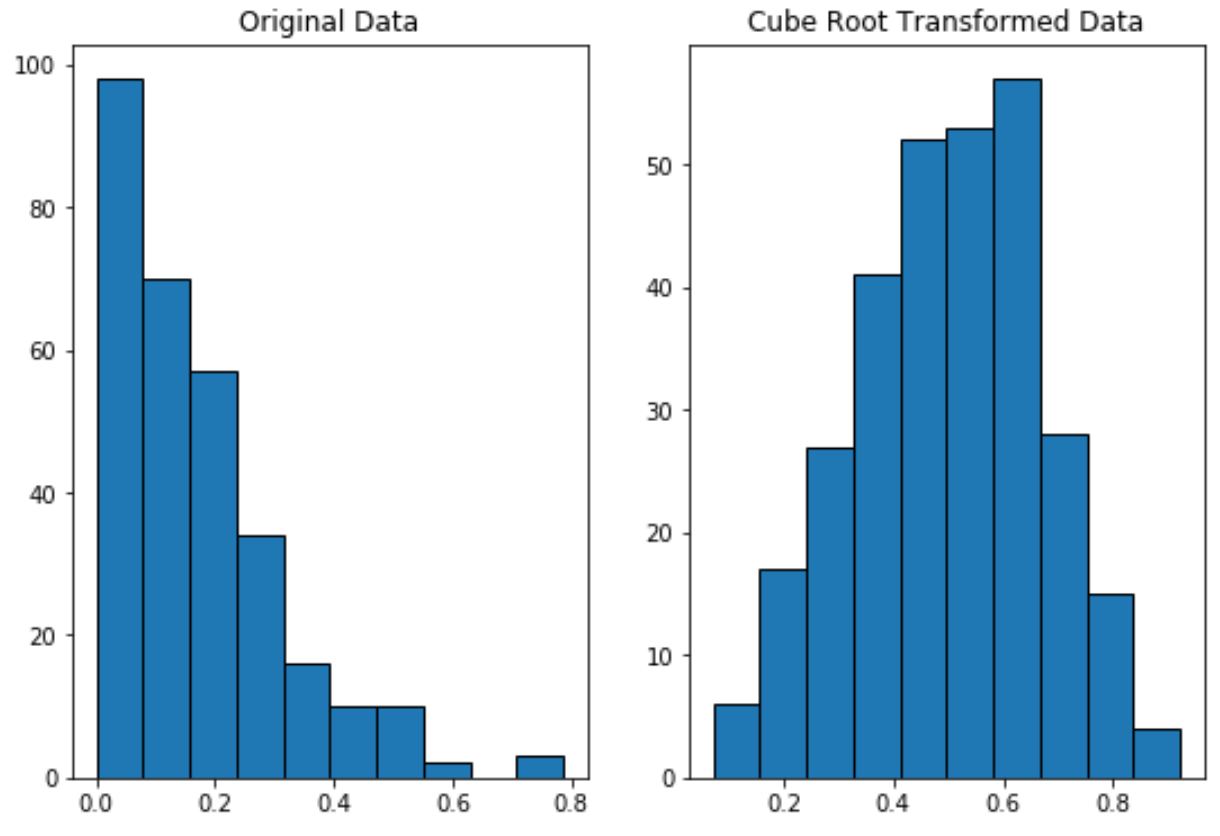
Remarquez comment les données transformées en racine cubique sont beaucoup plus normalement distribuées que les données d’origine.
Ressources additionnelles
Comment calculer les scores Z en Python
Comment normaliser les données en Python
Qu’est-ce que l’hypothèse de normalité en statistique ?
