Rapport de cotes par rapport au risque relatif : quelle est la différence ?

Deux termes que les étudiants confondent souvent dans les statistiques sont le rapport de cotes et le risque relatif .

Nous utilisons souvent ces deux métriques lors d’une analyse sur un tableau 2 par 2, qui prend le format suivant :

L’ odds ratio nous indique le rapport entre la probabilité qu’un événement se produise dans un groupe de traitement et la probabilité qu’un événement se produise dans un groupe témoin. Il est calculé comme suit :

Rapport de cotes = (A*D) / (B*C)

Le risque relatif nous indique le rapport entre la probabilité qu’un événement se produise dans un groupe de traitement et la probabilité qu’un événement se produise dans un groupe témoin. Il est calculé comme suit :

Risque relatif = [A/(A+B)] / [C/(C+D)]

Bref, voici la différence :

• Un rapport de cotes est un rapport de deux cotes .
• Le risque relatif est un rapport de deux probabilités .

L’exemple suivant montre comment calculer et interpréter un rapport de cotes et un risque relatif dans une situation réelle.

Exemple : calcul du rapport de cotes et du risque relatif

Supposons que 100 joueurs de basket-ball utilisent un nouveau programme d’entraînement et que 100 joueurs utilisent un ancien programme d’entraînement. À la fin du programme, nous testons chaque joueur pour voir s’il réussit un certain test de compétences.

Le tableau suivant montre le nombre de joueurs qui ont réussi et échoué, en fonction du programme qu’ils ont utilisé :

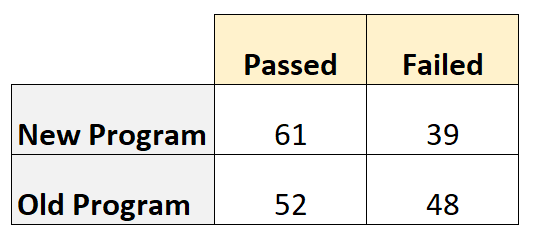
L’ odds ratio est calculé comme suit :

• Rapport de cotes = (A*D) / (B*C)
• Rapport de cotes = (61*48) / (39*52)
• Rapport de cotes = 1,44

Nous interpréterions cela comme signifiant que les chances qu’un joueur réussisse le test en utilisant le nouveau programme sont 1,44 fois les chances qu’un joueur réussisse le test en utilisant l’ancien programme.

En d’autres termes, les chances qu’un joueur réussisse le test augmentent grâce à l’utilisation du nouveau programme.

Le risque relatif est calculé comme

• Risque relatif = [A/(A+B)] / [C/(C+D)]
• Risque relatif = [61/(61+39)] / [52/(52+48)]
• Risque relatif = 1,17

Nous interpréterions cela comme signifiant que le rapport entre la probabilité qu’un joueur réussisse le test en utilisant le nouveau programme et l’ancien programme est de 1,17 .

Puisque cette valeur est supérieure à 1, cela nous indique que la probabilité de réussite est plus élevée dans le nouveau programme que dans l’ancien programme.

On peut aussi le constater en calculant directement la probabilité qu’un joueur passe sous chaque programme :

Probabilité de réussite sous nouveau programme = 61 / 100 = 61%

Probabilité de réussite sous ancien programme = 52 / 100 = 52%

En prenant le rapport de ces probabilités, nous pouvons calculer le risque relatif comme 61% / 52% = 1,17 .

Notez que l’odds ratio et le risque relatif sont tous deux supérieurs à 1, ce qui nous indique que les chances de vivre un événement (par exemple réussir le test de compétences) sont plus grandes dans le groupe de traitement que dans le groupe témoin.

Le rapport de cotes et le risque relatif nous donnent des informations similaires, mais nous interprétons chaque valeur de manière légèrement différente.

En particulier:

• Le rapport de cotes nous indique que les chances de réussir le test de compétences sont plus élevées dans le cadre du nouveau programme.
• Le risque relatif nous indique que la probabilité de réussir le test de compétences est plus élevée dans le cadre du nouveau programme.

En utilisant l’une ou l’autre métrique, nous pouvons facilement voir que le nouveau programme est meilleur que l’ancien.

Ressources additionnelles

Les didacticiels suivants offrent des informations supplémentaires sur les rapports de cotes et le risque relatif :

Comment interpréter les rapports de cotes
Comment interpréter le risque relatif
Comment calculer le rapport de cotes et le risque relatif dans Excel