Comment calculer la variance d’une distribution de probabilité

Une distribution de probabilité nous indique la probabilité qu’une variable aléatoire prenne certaines valeurs.

Par exemple, la distribution de probabilité suivante nous indique la probabilité qu’une certaine équipe de football marque un certain nombre de buts dans un match donné :

Pour trouver la variance d’une distribution de probabilité, nous pouvons utiliser la formule suivante :

σ ² = Σ(x _je -μ) ² * P(x _je )

où:

• x _i : La ^ième valeur
• μ : La moyenne de la distribution
• P(x _i ) : La probabilité de la ^ième valeur

Par exemple, considérons notre distribution de probabilité pour l’équipe de football :

Le nombre moyen de buts de l’équipe de football serait calculé comme suit :

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 buts.

Nous pourrions alors calculer la variance comme suit :

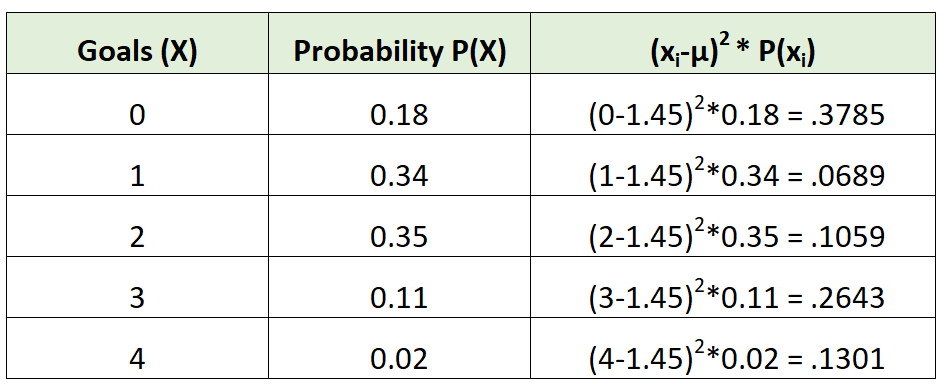
La variance est simplement la somme des valeurs de la troisième colonne. Ainsi, nous le calculerions comme suit :

σ ² = 0,3785 + 0,0689 + 0,1059 + 0,2643 + 0,1301 = 0,9475

Les exemples suivants montrent comment calculer la variance d’une distribution de probabilité dans quelques autres scénarios.

Exemple 1 : Variation des pannes de véhicules

La distribution de probabilité suivante nous indique la probabilité qu’un véhicule donné subisse un certain nombre de pannes de batterie sur une période de 10 ans :

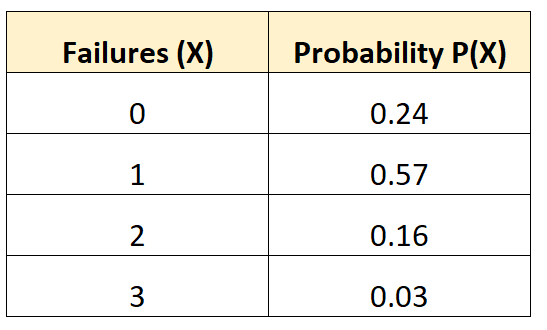
Pour trouver la variance de cette distribution de probabilité, nous devons d’abord calculer le nombre moyen de défaillances attendues :

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 échecs.

Nous pourrions alors calculer la variance comme suit :

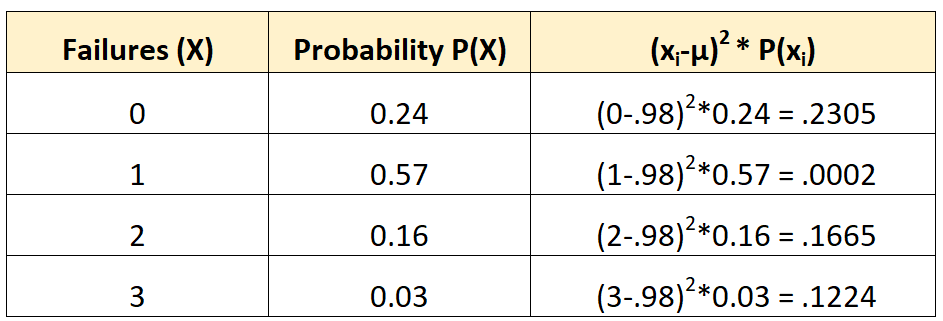
La variance est la somme des valeurs de la troisième colonne. Ainsi, nous le calculerions comme suit :

σ ² = 0,2305 + 0,0002 + 0,1665 + 0,1224 = 0,5196

Exemple 2 : Variation des ventes

La distribution de probabilité suivante nous indique la probabilité qu’un vendeur donné réalise un certain nombre de ventes au cours du mois à venir :

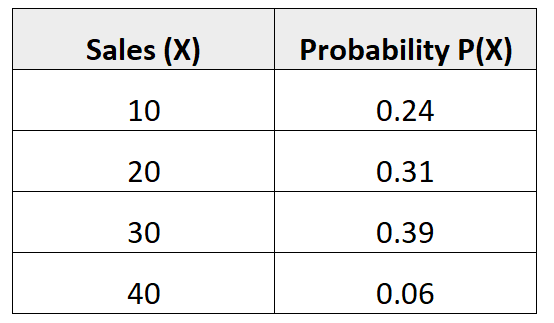
Pour trouver la variance de cette distribution de probabilité, nous devons d’abord calculer le nombre moyen de ventes attendues :

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 ventes.

Nous pourrions alors calculer la variance comme suit :

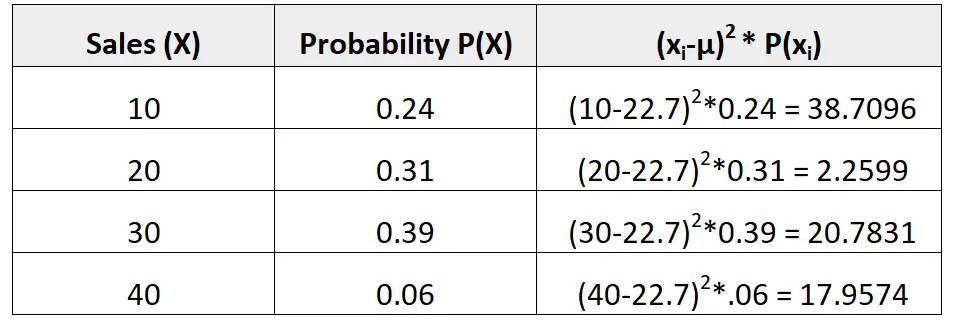
La variance est la somme des valeurs de la troisième colonne. Ainsi, nous le calculerions comme suit :

σ ² = 38,7096 + 2,2599 + 20,7831 + 17,9574 = 79,71

Notez que nous pourrions également utiliser le calculateur de distribution de probabilité pour calculer automatiquement la variance de cette distribution :

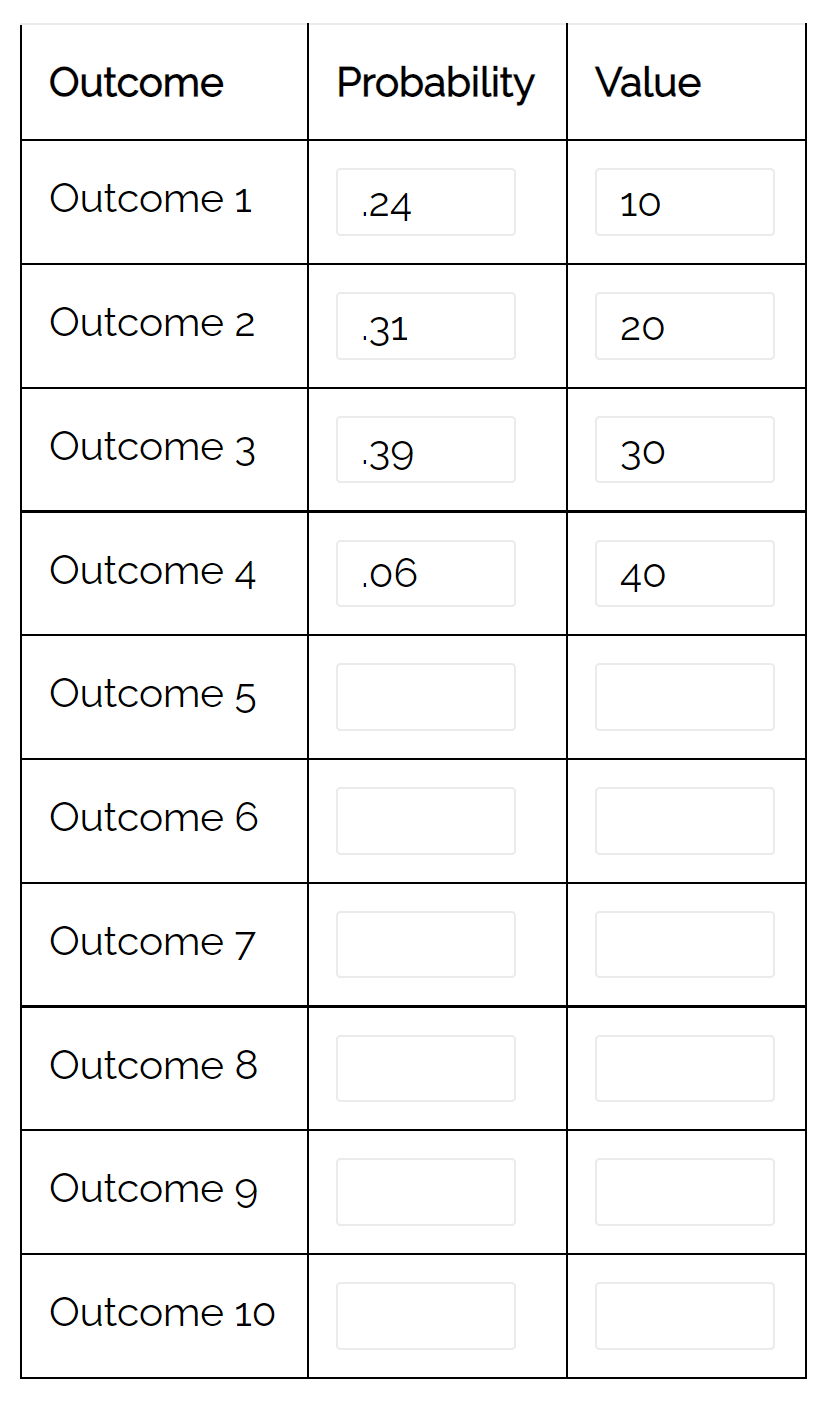
L’écart est de 79,71 . Cela correspond à la valeur que nous avons calculée manuellement.