T-Score vs Z-Score : quand les utiliser ?

Deux termes qui déroutent souvent les étudiants dans les cours de statistiques sont les scores t et les scores z .

Les deux sont largement utilisés lors de la réalisation de tests d’hypothèses ou de la construction d’intervalles de confiance , mais ils sont légèrement différents.

Voici la formule pour chacun :

score t = ( x – μ) / (s/√ n )

où:

• x : moyenne de l’échantillon
• μ : Moyenne de la population
• s : Écart type de l’échantillon
• n : Taille de l’échantillon

Score z = ( x – μ) / σ

où:

• x : Valeur des données brutes
• μ : Moyenne de la population
• σ : Écart type de population

Cet organigramme montre quand vous devez utiliser chacun d’entre eux, en fonction de vos données :

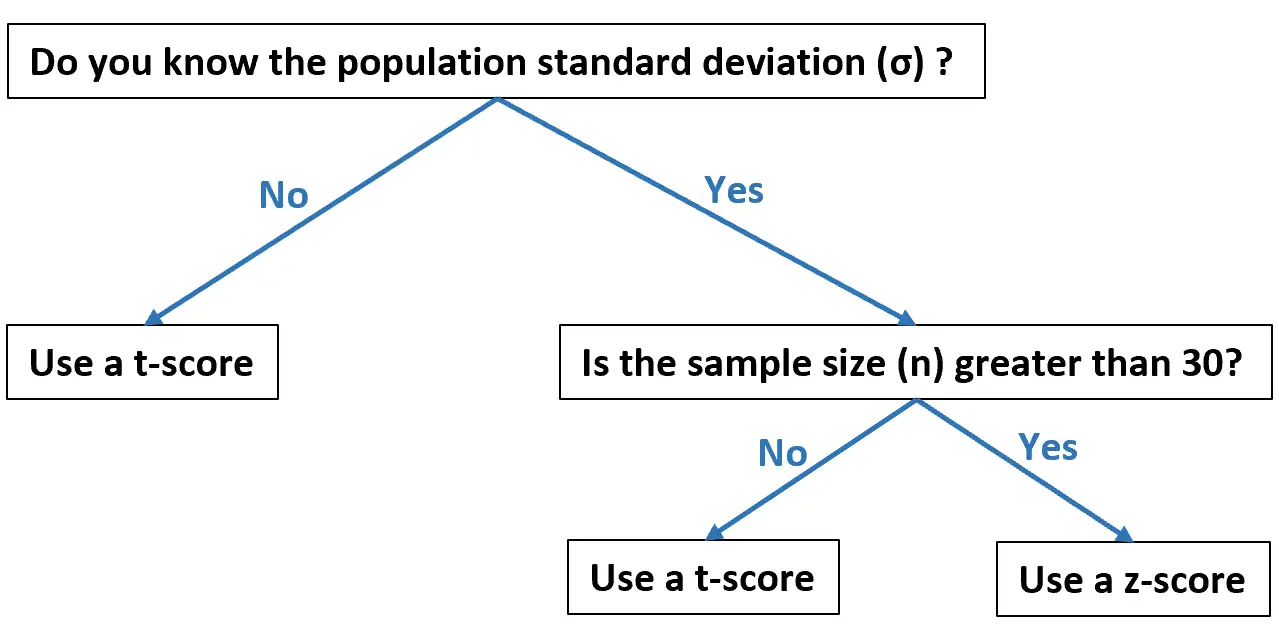
Les exemples suivants montrent comment calculer un score T et un score Z en pratique.

Exemple 1 : Calcul d’un T-Score

Supposons qu’un restaurant prépare des hamburgers prétendant avoir un poids moyen de μ = 0,25 livre.

Supposons que nous prenions un échantillon aléatoire de n = 20 hamburgers et que nous constations que le poids moyen de l’échantillon est x = 0,22 livre avec un écart type de s = 0,05 livre. Effectuez un test d’hypothèse pour déterminer si le poids moyen réel de tous les hamburgers produits par ce restaurant est égal à 0,25 livre.

Pour cet exemple, nous utiliserions un score T pour effectuer le test d’hypothèse car aucune des deux conditions suivantes n’est remplie.

• L’écart type de la population (σ) est connu. (σ n’est pas fourni dans cet exemple)
• La taille de l’échantillon est supérieure à 30. (n = 20 dans cet exemple)

Ainsi, nous calculerions le t-score comme suit :

• score t = ( x – μ) / (s/√ n )
• score t = (0,22 – 0,25) / (0,05 / √ 20 )
• score t = -2,68

Selon le calculateur de score T à valeur P , la valeur p qui correspond à ce score t est de 0,01481 .

Puisque cette valeur p est inférieure à 0,05, nous disposons de preuves suffisantes pour affirmer que le poids moyen des hamburgers produits dans ce restaurant n’est pas égal à 0,25 livre.

Exemple 2 : Calcul d’un score Z

Supposons qu’une entreprise fabrique des batteries dont on sait que leur durée de vie suit une distribution normale avec une moyenne de μ = 20 heures et un écart type de σ = 5 heures.

Supposons que nous prenions un échantillon aléatoire de n = 50 piles et que nous constations que la moyenne de l’échantillon est x = 21 heures. Effectuez un test d’hypothèse pour déterminer si la véritable durée de vie moyenne de toutes les batteries fabriquées par cette société est égale à 20 heures.

Pour cet exemple, nous utiliserions un score z pour effectuer le test d’hypothèse car les deux conditions suivantes sont remplies :

• L’écart type de la population (σ) est connu. (σ est égal à 5 dans cet exemple)
• La taille de l’échantillon est supérieure à 30. (n = 50 dans cet exemple)

Ainsi, nous calculerions le z-score comme suit :

• Score z = ( x – μ) / σ
• Score z = (21 – 20) / 5
• score z = 0,2

Selon lecalculateur de score Z à valeur P , la valeur p qui correspond à ce score z est de 0,84184 .

Étant donné que cette valeur p n’est pas inférieure à 0,05, nous ne disposons pas de preuves suffisantes pour affirmer que la durée de vie moyenne de toutes les batteries fabriquées par cette société est différente de 20 heures.

Ressources additionnelles

Les didacticiels suivants offrent plus d’informations sur les scores T et les scores Z :

Distribution normale vs distribution t : quelle est la différence ?
Comment lire le tableau de distribution t
Comment lire la table Z