Les 3 types de régression logistique (y compris des exemples)

La régression logistique fait référence à tout modèle de régression dans lequel la variable de réponse est catégorielle.

Il existe trois types de modèles de régression logistique :

• Régression logistique binaire : La variable réponse ne peut appartenir qu’à l’une des deux catégories.
• Régression logistique multinomiale : la variable de réponse peut appartenir à l’une des trois catégories ou plus et il n’y a pas d’ordre naturel entre les catégories.
• Régression logistique ordinale : la variable de réponse peut appartenir à l’une des trois catégories ou plus et il existe un ordre naturel entre les catégories.

Le tableau suivant résume ces différences :

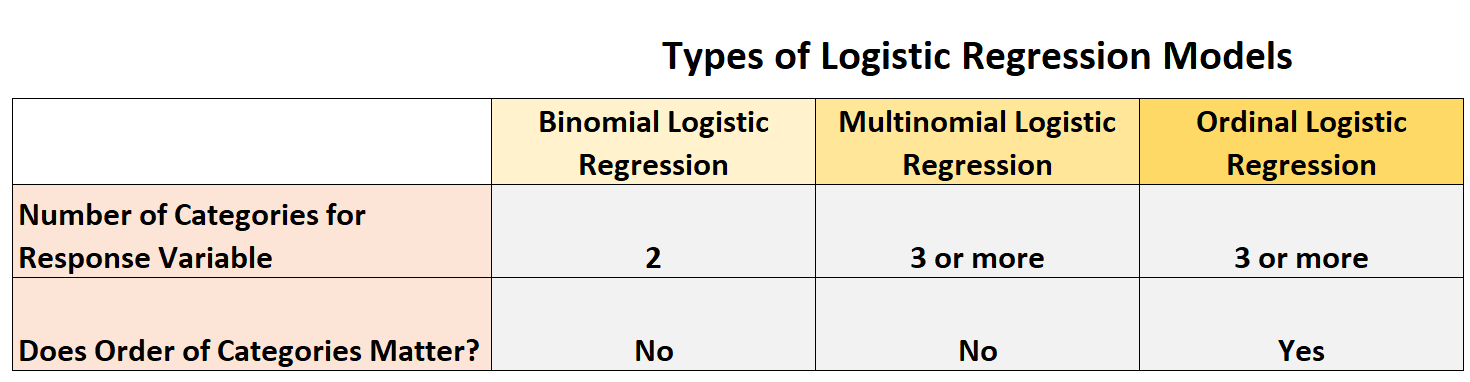
Ce didacticiel fournit une brève explication de chaque type de modèle de régression logistique ainsi que des exemples de chacun.

Type n°1 : régression logistique binaire

Les modèles de régression logistique binaire sont un type de régression logistique dans lequel la variable de réponse ne peut appartenir qu’à deux catégories.

Voici quelques exemples :

Exemple 1 : Draft NBA

Supposons qu’un scientifique des données sportives souhaite utiliser les variables prédictives (1) points, (2) rebonds et (3) aides pour prédire la probabilité qu’un joueur de basket-ball universitaire donné soit recruté dans la NBA.

Puisqu’il n’y a que deux résultats possibles (rédigés ou non) pour la variable de réponse, le data scientist utiliserait un modèle de régression logistique binomiale.

Exemple 2 : Détection de spam

Supposons qu’une entreprise souhaite utiliser les variables prédictives (1) nombre de mots et (2) pays d’origine pour prédire la probabilité qu’un e-mail donné soit du spam.

Puisqu’il n’y a que deux résultats possibles (spam ou non-spam) pour la variable de réponse, l’entreprise utiliserait un modèle de régression logistique binomiale.

Type n°2 : Régression logistique multinomiale

Les modèles de régression logistique multinomiale sont un type de régression logistique dans lequel la variable de réponse peut appartenir à l’une des trois catégories ou plus et il n’y a pas d’ordre naturel entre les catégories.

Voici quelques exemples :

Exemple 1 : Préférence politique

Supposons qu’un politologue souhaite utiliser les variables prédictives (1) le revenu annuel et (2) les années d’études pour prédire la probabilité qu’un individu vote pour l’un des quatre candidats présidentiels différents.

Puisqu’il y a plus de deux résultats possibles (il y a quatre candidats potentiels) pour la variable de réponse et qu’il n’y a pas d’ordre naturel entre les résultats, le politologue utiliserait un modèle de régression logistique multinomiale.

Exemple 2 : Préférence sportive

Supposons qu’un analyste sportif souhaite utiliser les variables prédictives (1) les heures de télévision regardées par semaine et (2) l’âge pour prédire la probabilité qu’un individu choisisse le basket-ball, le football ou le baseball comme sport préféré.

Puisqu’il existe plus de deux résultats possibles (il existe trois sports) pour la variable de réponse, l’analyste sportif utilisera un modèle de régression logistique multinomiale.

Type n°3 : Régression logistique ordinale

Les modèles de régression logistique ordinale sont un type de régression logistique dans lequel la variable de réponse peut appartenir à l’une des trois catégories ou plus et il existe un ordre naturel entre les catégories.

Voici quelques exemples :

Exemple 1 : évaluations scolaires

Supposons qu’un conseiller pédagogique souhaite utiliser les variables prédictives (1) GPA, (2) score ACT et (3) score SAT pour prédire la probabilité qu’un individu entre dans une université qui peut être classée dans les catégories « mauvaise », « médiocre ». », « bon » ou « génial ».

Puisqu’il existe plus de deux résultats possibles (il existe quatre classifications de la qualité de l’école) pour la variable de réponse et qu’il existe un ordre naturel entre les résultats, le conseiller pédagogique utiliserait un modèle de régression logistique ordinale.

Exemple 2 : Classements de films

Supposons qu’un critique de cinéma souhaite utiliser les variables prédictives (1) durée totale d’exécution et (2) genre pour prédire la probabilité qu’un film donné reçoive une note comprise entre 1 et 10.

Puisqu’il y a plus de deux résultats possibles (il y a 10 évaluations possibles) pour la variable de réponse et qu’il existe un ordre naturel entre les résultats, le critique de cinéma utiliserait un modèle de régression logistique ordinale.

Ressources additionnelles

Les didacticiels suivants fournissent plus de détails sur les modèles de régression logistique :

Introduction à la régression logistique
Les 6 hypothèses de la régression logistique
4 exemples d’utilisation de la régression logistique dans la vie réelle