Comment utiliser la fonction lm() dans R pour ajuster des modèles linéaires

La fonction lm() dans R est utilisée pour ajuster les modèles de régression linéaire.

Cette fonction utilise la syntaxe de base suivante :

lm(formule, données, …)

où:

• formule : La formule du modèle linéaire (par exemple y ~ x1 + x2)
• data : Le nom du bloc de données qui contient les données

L’exemple suivant montre comment utiliser cette fonction dans R pour effectuer les opérations suivantes :

• Ajuster un modèle de régression
• Afficher le résumé de l’ajustement du modèle de régression
• Afficher les tracés de diagnostic du modèle
• Tracez le modèle de régression ajusté
• Faire des prédictions à l’aide du modèle de régression

Ajuster le modèle de régression

Le code suivant montre comment utiliser la fonction lm() pour ajuster un modèle de régression linéaire dans R :

#define data
df = data.frame(x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

Afficher le résumé du modèle de régression

Nous pouvons ensuite utiliser la fonction summary() pour afficher le résumé de l’ajustement du modèle de régression :

#view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.4793 -0.9772 -0.4772  1.4388  4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  11.1432     1.9104   5.833  0.00039 ***
x             1.2780     0.2984   4.284  0.00267 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared:  0.6964,	Adjusted R-squared:  0.6584 
F-statistic: 18.35 on 1 and 8 DF,  p-value: 0.002675

Voici comment interpréter les valeurs les plus importantes du modèle :

• Statistique F = 18,35, valeur p correspondante = 0,002675. Puisque cette valeur p est inférieure à 0,05, le modèle dans son ensemble est statistiquement significatif.
• R au carré multiple = 0,6964. Cela nous indique que 69,64 % de la variation de la variable de réponse, y, peut être expliquée par la variable prédictive, x.
• Estimation du coefficient de x : 1,2780. Cela nous indique que chaque augmentation supplémentaire d’une unité de x est associée à une augmentation moyenne de 1,2780 de y.

Nous pouvons ensuite utiliser les estimations de coefficients de la sortie pour écrire l’équation de régression estimée :

y = 11,1432 + 1,2780*(x)

Bonus : vous pouvez trouver un guide complet pour interpréter chaque valeur de la sortie de régression dans R ici .

Afficher les tracés de diagnostic du modèle

Nous pouvons ensuite utiliser la fonction plot() pour tracer les tracés de diagnostic du modèle de régression :

#create diagnostic plots
plot(model)

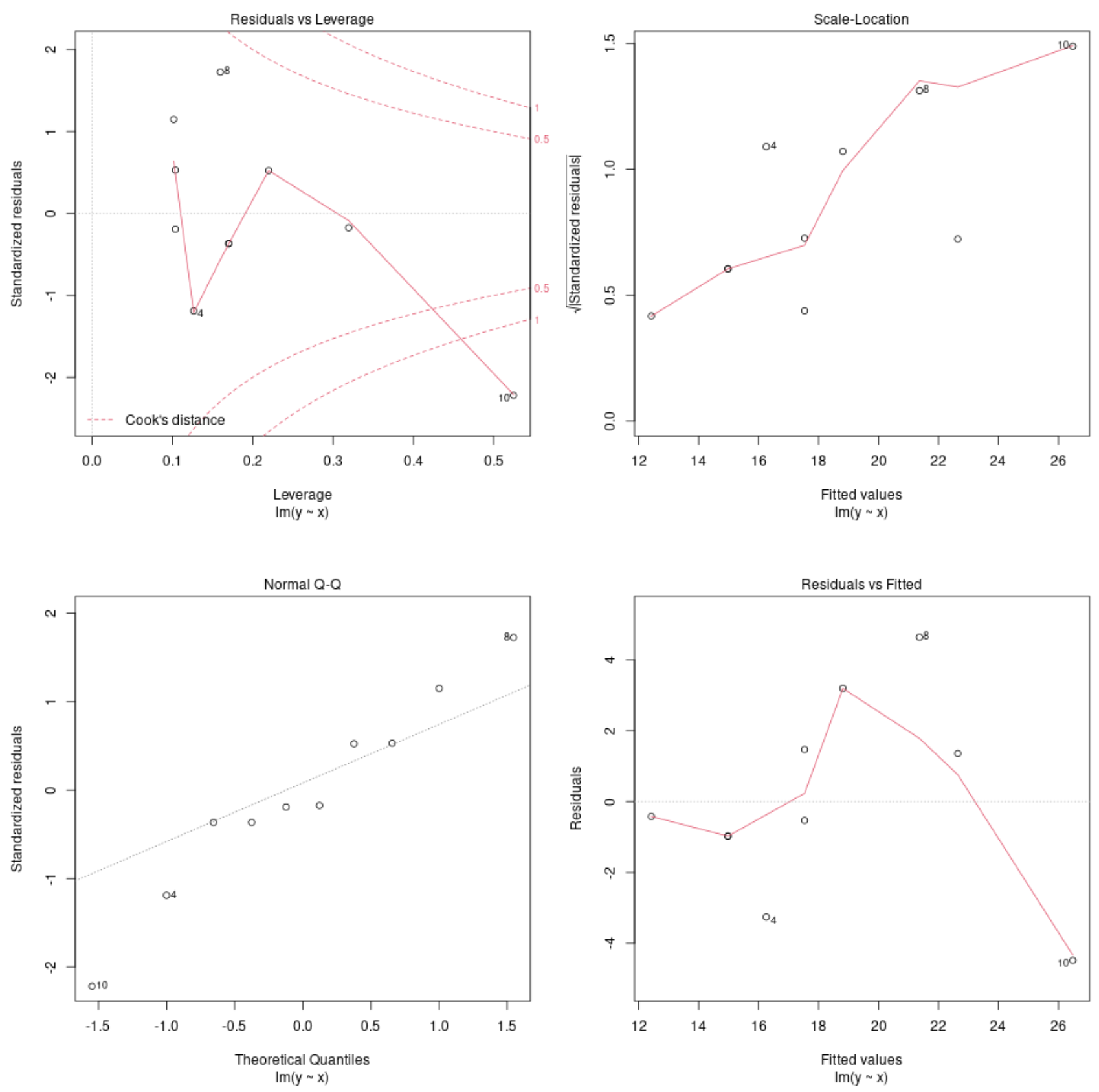
Ces graphiques nous permettent d’analyser les résidus du modèle de régression pour déterminer si le modèle est approprié à utiliser pour les données.

Reportez-vous à ce didacticiel pour une explication complète de la façon d’interpréter les tracés de diagnostic d’un modèle dans R.

Tracer le modèle de régression ajusté

Nous pouvons utiliser la fonction abline() pour tracer le modèle de régression ajusté :

#create scatterplot of raw data
plot(df$x, df$y, col='red', main='Summary of Regression Model', xlab='x', ylab='y')

#add fitted regression line
abline(model)

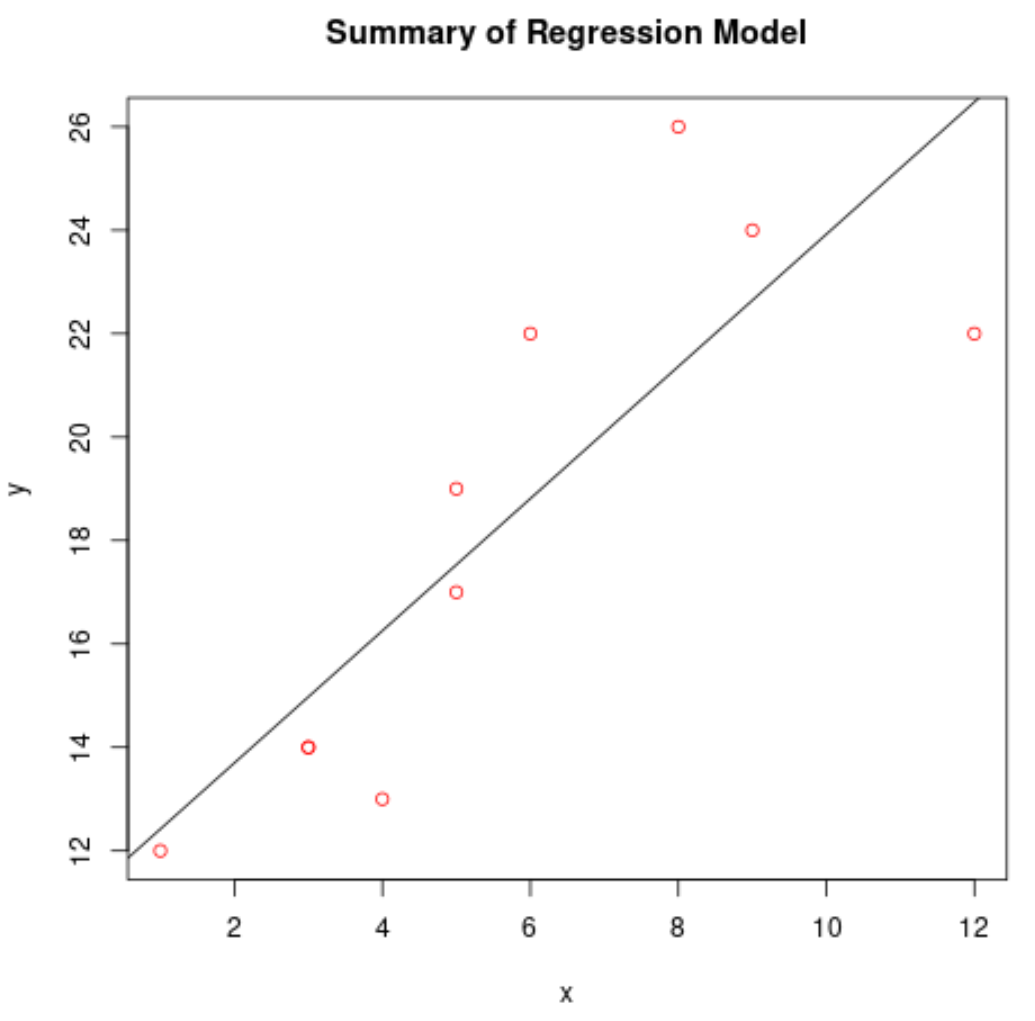
Utilisez le modèle de régression pour faire des prédictions

Nous pouvons utiliser la fonction prédire() pour prédire la valeur de réponse pour une nouvelle observation :

#define new observation
new <- data.frame(x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332 

Le modèle prédit que cette nouvelle observation aura une valeur de réponse de 17,5332 .

Ressources additionnelles

Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression pas à pas dans R