Pourquoi la médiane est-elle importante dans les statistiques ?

La médiane représente la valeur médiane d’un ensemble de données, lorsque toutes les valeurs sont classées de la plus petite à la plus grande.

Par exemple, la médiane dans l’ensemble de données suivant est 19 :

Ensemble de données : 3, 4, 11, 15, 19 , 22, 23, 23, 26

La médiane représente également le 50 ^e percentile d’un ensemble de données. Autrement dit, exactement la moitié des valeurs de l’ensemble de données sont supérieures à la médiane et la moitié des valeurs sont inférieures.

La médiane est une mesure importante à calculer car elle nous donne une idée de l’endroit où se trouve le « centre » d’un ensemble de données. Cela nous donne également une idée de la valeur « typique » dans un ensemble de données donné.

Par exemple, supposons que nous disposions d’un ensemble de données contenant le prix de vente de 10 000 maisons différentes dans une certaine ville.

Au lieu de regarder des rangées et des rangées de données brutes , nous pouvons calculer la valeur médiane pour comprendre rapidement le prix de vente moyen des maisons dans cette ville.

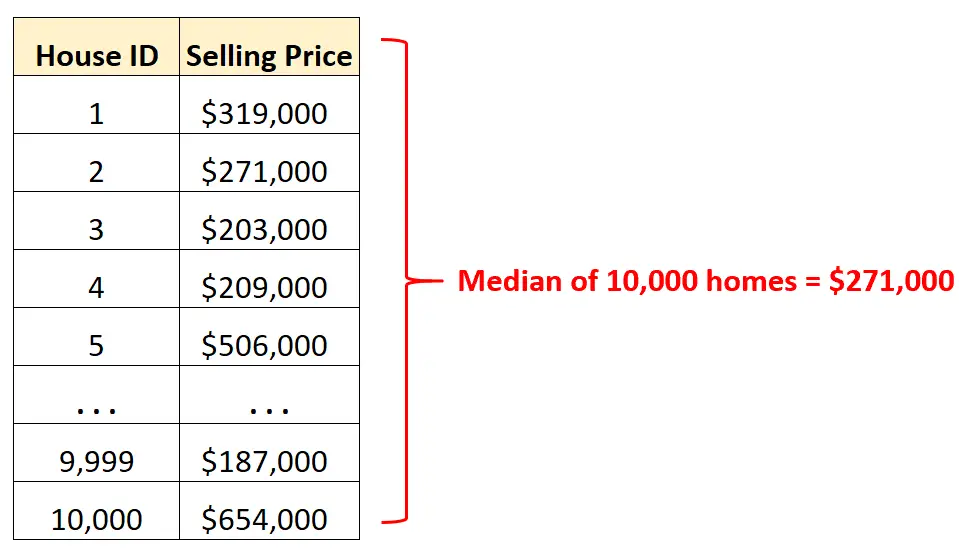
En sachant que le prix de vente médian est de 271 000 $, nous savons qu’exactement la moitié des 10 000 maisons se sont vendues à un prix supérieur à ce montant et l’autre moitié à un prix inférieur.

Cela nous donne également une idée du prix de vente « typique » des maisons dans cette ville.

Quand utiliser la médiane

Lors de l’analyse d’ensembles de données, nous souhaitons souvent comprendre où se situe la valeur centrale.

En statistiques, il existe deux métriques courantes que nous utilisons pour mesurer le centre d’un ensemble de données :

• Moyenne : la valeur moyenne dans un ensemble de données
• Médiane : La valeur médiane dans un ensemble de données

Il s’avère que la médiane est une mesure plus utile dans les circonstances suivantes :

• Quand la distribution est asymétrique .
• Lorsque la distribution contient des valeurs aberrantes.

Pour illustrer cela, considérons les deux exemples suivants.

Exemple 1 : Calcul de la médiane d’une distribution asymétrique

Considérez la répartition suivante des salaires pour les résidents d’une certaine ville :

La médiane rend mieux compte du salaire « typique » d’un résident que la moyenne, car la répartition est asymétrique vers la droite.

Cela signifie que les salaires élevés du côté droit de la distribution éloignent la moyenne du centre de la distribution.

Dans cet exemple particulier, le salaire moyen est de 47 000 $ tandis que le salaire médian est de 32 000 $. La médiane est beaucoup plus représentative du salaire type dans cette ville.

Exemple 2 : Calcul de la médiane en présence de valeurs aberrantes

Considérez le graphique suivant qui montre la superficie en pieds carrés des maisons dans une certaine rue :

La moyenne est fortement influencée par quelques maisons extrêmement grandes, alors que la médiane ne l’est pas.

Nous pouvons voir que la médiane parvient mieux à capturer la superficie « typique » d’une maison dans cette rue que la moyenne, car elle n’est pas influencée par les valeurs extrêmes.

Résumé

Voici un bref résumé des principaux points abordés dans cet article :

• La médiane représente la valeur médiane dans un ensemble de données.
• La médiane est importante car elle nous donne une idée de l’endroit où se situe la valeur centrale dans un ensemble de données.
• La médiane a tendance à être plus utile à calculer que la moyenne lorsqu’une distribution est asymétrique et/ou comporte des valeurs aberrantes.

Ressources additionnelles

Exemples concrets : utilisation de la moyenne, de la médiane et du mode
Quand utiliser la moyenne par rapport à la médiane : avec des exemples
Pourquoi le mode est-il important dans les statistiques ?