Qu’est-ce que cela signifie si une statistique est résistante ?

Une statistique est dite résistante si elle n’est pas sensible aux valeurs extrêmes.

Voici deux exemples de statistiques résistantes :

• La médiane
• L’intervalle interquartile

Voici des exemples de statistiques qui ne résistent pas :

• La moyenne
• L’écart type
• La gamme

L’exemple suivant illustre la différence entre les statistiques résistantes et non résistantes.

Exemple : Statistiques résistantes et non résistantes

Supposons que nous ayons l’ensemble de données suivant :

Ensemble de données : 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29

À l’aide d’une calculatrice ou d’un logiciel statistique, nous pouvons calculer la valeur des statistiques résistantes suivantes pour cet ensemble de données :

• Médiane : 13
• Écart interquartile : 13,5

Nous pouvons également calculer la valeur des statistiques non résistantes suivantes pour cet ensemble de données :

• Moyenne : 13,54
• Écart type : 8,82
• Portée : 27

Considérez maintenant si cet ensemble de données comportait une valeur aberrante extrême ajoutée :

Ensemble de données : 2, 5, 6, 7, 8, 13, 15, 18, 22, 24, 29, 450

Nous pouvons à nouveau calculer la valeur des statistiques résistantes suivantes pour cet ensemble de données :

• Médiane : 14
• Écart interquartile : 15,75

Nous pouvons également calculer la valeur des statistiques non résistantes suivantes pour cet ensemble de données :

• Moyenne : 49,92
• Écart type : 126,27
• Portée : 448

Remarquez à quel point les statistiques de non-résistance ont changé en ajoutant simplement une valeur extrême à l’ensemble de données :

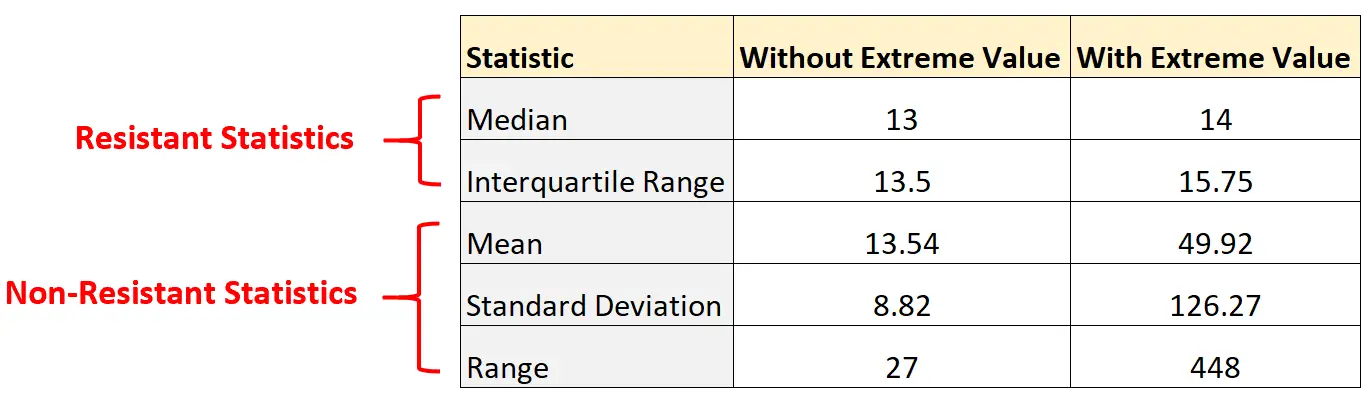
À l’inverse, les statistiques des résistants n’ont pratiquement pas changé. La médiane et l’intervalle interquartile n’ont que légèrement changé.

Quand utiliser les statistiques résistantes

Les statistiques les plus couramment utilisées pour mesurer le centre et la dispersion des valeurs dans un ensemble de données sont respectivement la moyenne et l’écart type.

Malheureusement, ces deux statistiques sont sensibles aux valeurs extrêmes. Ainsi, si des valeurs aberrantes sont présentes dans un ensemble de données, la moyenne et l’écart type ne décriront pas avec précision la distribution des valeurs dans un ensemble de données.

Au lieu de cela, il est recommandé d’utiliser la médiane et l’intervalle interquartile pour mesurer le centre et la dispersion des valeurs dans un ensemble de données si des valeurs aberrantes sont présentes, car ces deux statistiques sont résistantes .

Ressources additionnelles

Comment les valeurs aberrantes affectent-elles la moyenne ?
Quand utiliser la moyenne par rapport à la médiane
Quand utiliser l’intervalle interquartile par rapport à l’écart type