Comment calculer la médiane à partir du tableau de fréquence (avec exemples)

Vous pouvez trouver la valeur médiane d’un tableau de fréquences en procédant comme suit :

Étape 1 : Organisez toutes les valeurs individuelles de la plus petite à la plus grande.

Étape 2 : Identifiez la valeur directement au milieu de la liste ordonnée.

• S’il y a un nombre impair de valeurs, la médiane est la valeur directement au milieu.
• S’il existe un nombre pair de valeurs, la médiane est la moyenne des deux valeurs médianes.

Les exemples suivants montrent comment trouver la valeur médiane d’un tableau de fréquences en pratique.

Exemple 1 : Médiane du tableau de fréquence (nombre impair de valeurs)

Le tableau de fréquence suivant montre le nombre total de victoires pour 17 équipes de football dans une ligue donnée :

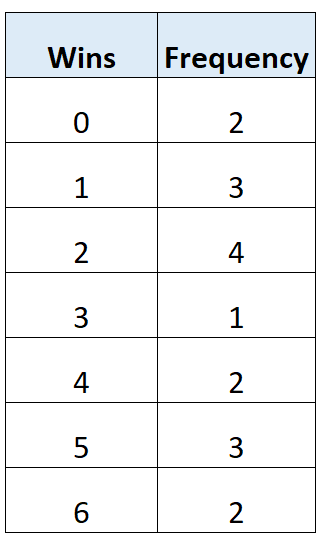
Nous pouvons utiliser les étapes suivantes pour trouver la valeur médiane dans ce tableau de fréquence :

Étape 1 : Organisez toutes les valeurs individuelles de la plus petite à la plus grande.

Valeurs : 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, 5, 5, 5, 6, 6

Étape 2 : Identifiez la valeur directement au milieu de la liste ordonnée.

Valeurs : 0, 0, 1, 1, 1, 2, 2, 2, 2 , 3, 4, 4, 5, 5, 5, 6, 6

La valeur médiane est 2 .

Exemple 2 : Médiane du tableau de fréquence (nombre pair de valeurs)

Le tableau de fréquence suivant montre la taille des ménages de 20 ménages différents dans une zone particulière :

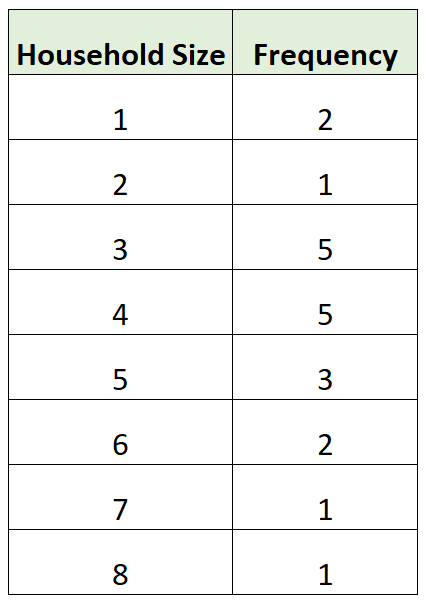
Nous pouvons utiliser les étapes suivantes pour trouver la valeur médiane dans ce tableau de fréquence :

Étape 1 : Organisez toutes les valeurs individuelles de la plus petite à la plus grande.

Valeurs : 1, 1, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8

Étape 2 : Identifiez la valeur directement au milieu de la liste ordonnée.

Valeurs : 1, 1, 2, 3, 3, 3, 3, 3, 4 , 4 , 4 , 4, 4, 5, 5, 5, 6, 6, 7, 8

Il y a deux valeurs situées directement au milieu : 4 et 4.

Ainsi, la valeur médiane est la moyenne de ces deux valeurs : (4 + 4) / 2 = 4 .

Ressources additionnelles

Comment calculer la moyenne à partir du tableau de fréquence
Comment calculer le mode à partir du tableau de fréquence
Comment estimer la moyenne et la médiane des histogrammes
Quand utiliser la moyenne par rapport à la médiane