Qu’est-ce qu’une relation monotone ? (Définition + Exemples)
En statistiques, une relation monotone entre deux variables fait référence à un scénario dans lequel un changement dans une variable est généralement associé à un changement dans une direction spécifique dans une autre variable.
Il existe deux types de relations monotones :
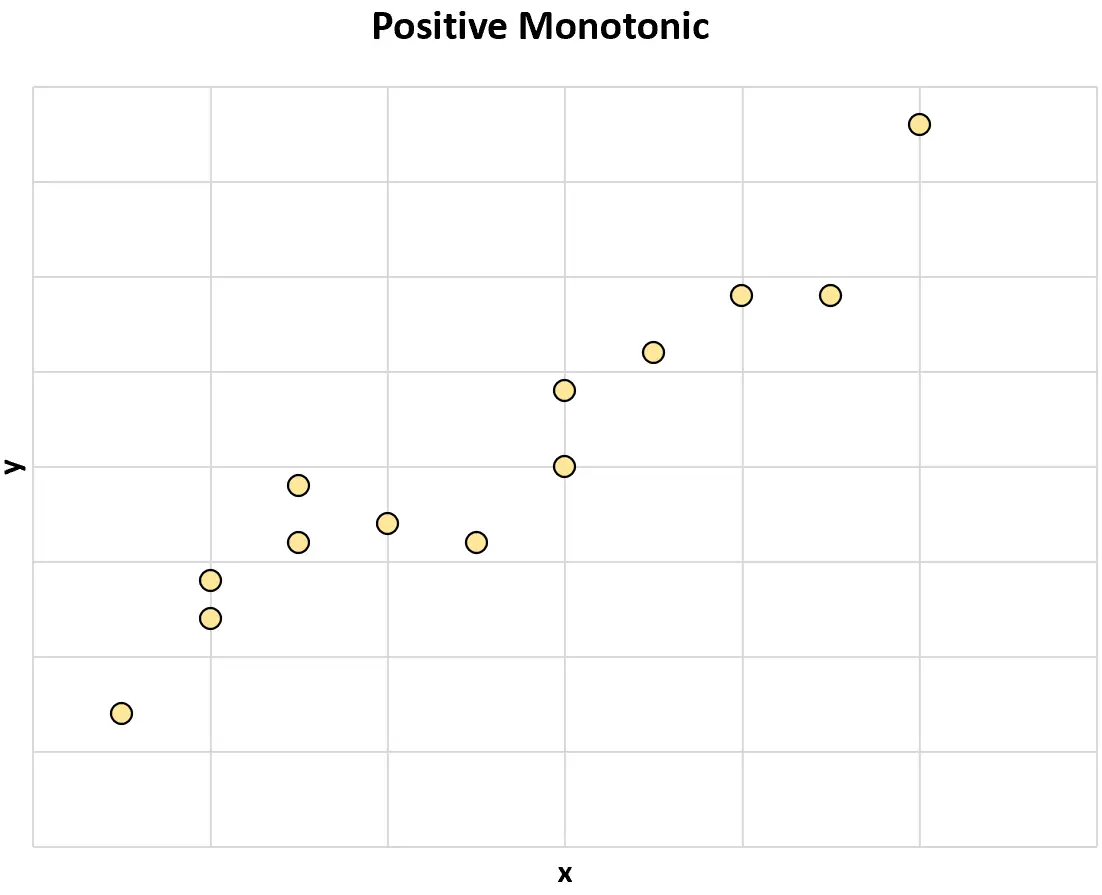
Monotone positif : lorsque la valeur d’une variable augmente, la valeur de l’autre variable a également tendance à augmenter.
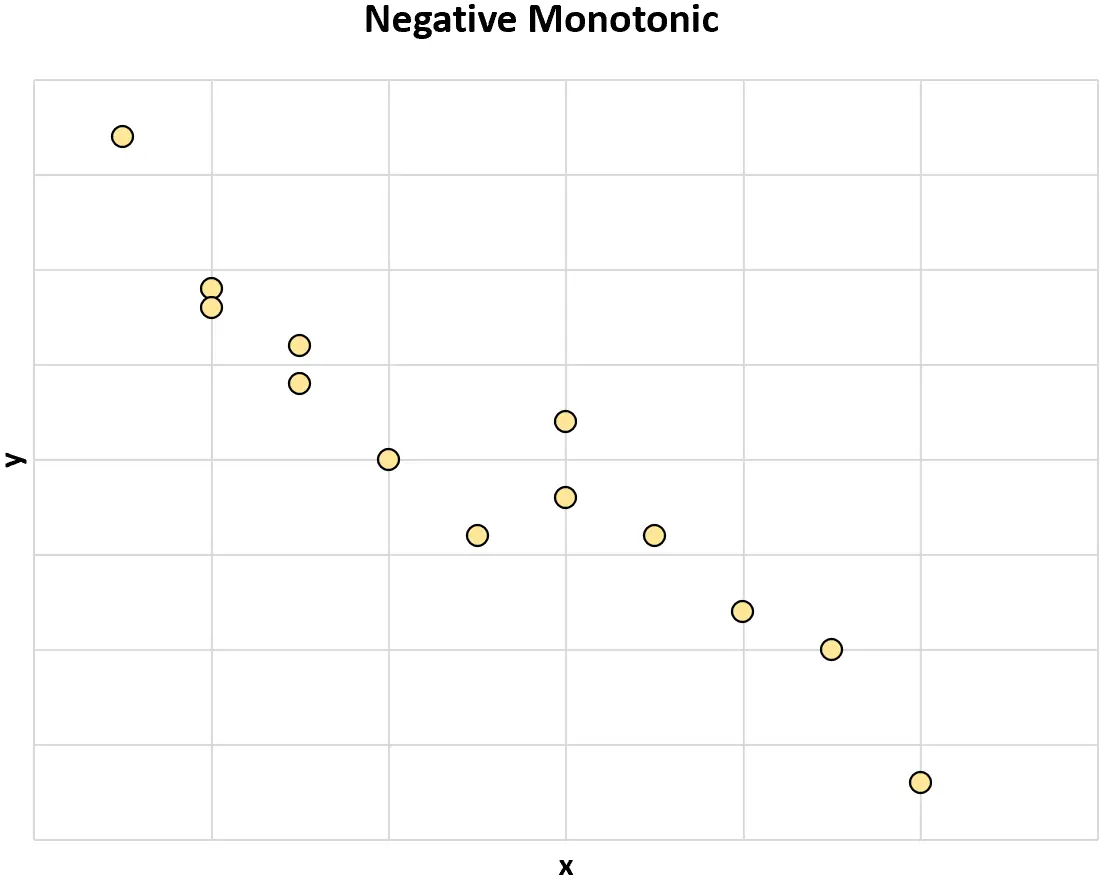
Monotone négatif : lorsque la valeur d’une variable augmente, la valeur de l’autre variable a tendance à diminuer.
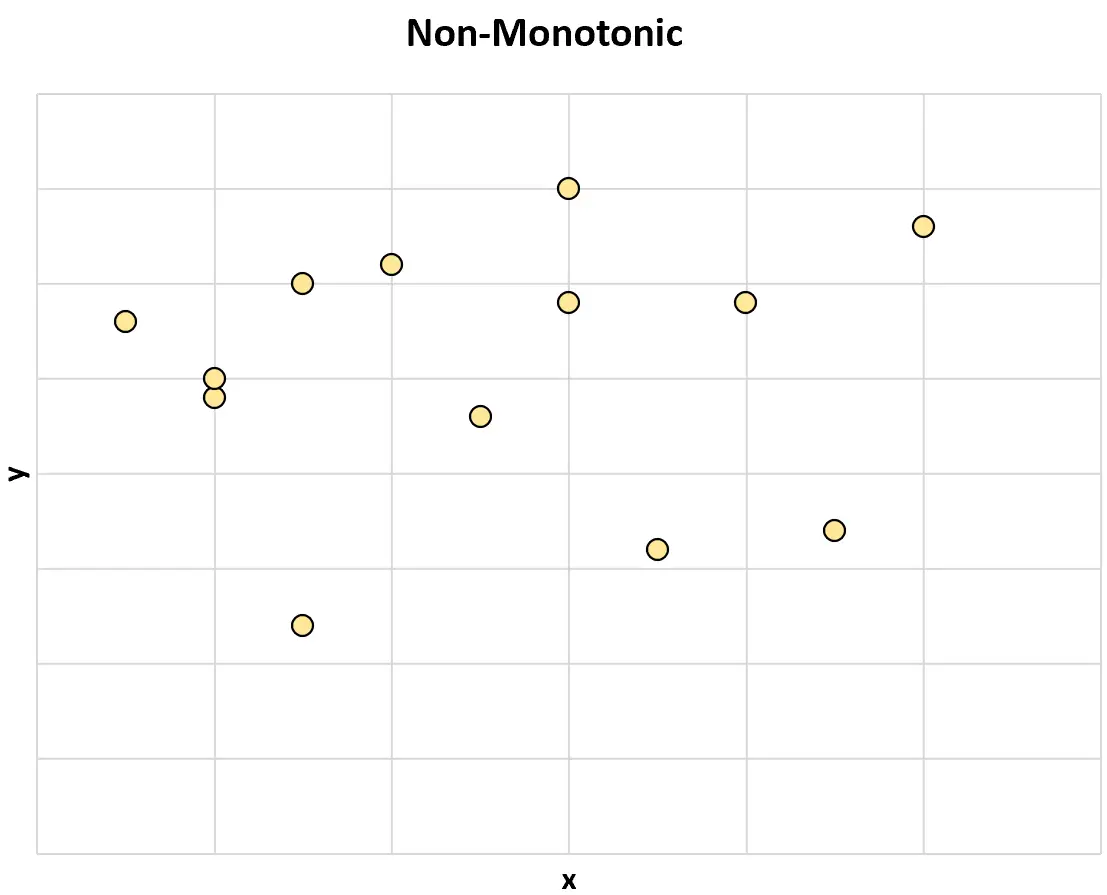
Si deux variables ne changent généralement pas dans la même direction, on dit alors qu’elles ont une relation non monotone .
Voici un exemple de relation non monotone entre deux variables :
Et voici un autre exemple de relation non monotone entre deux variables :
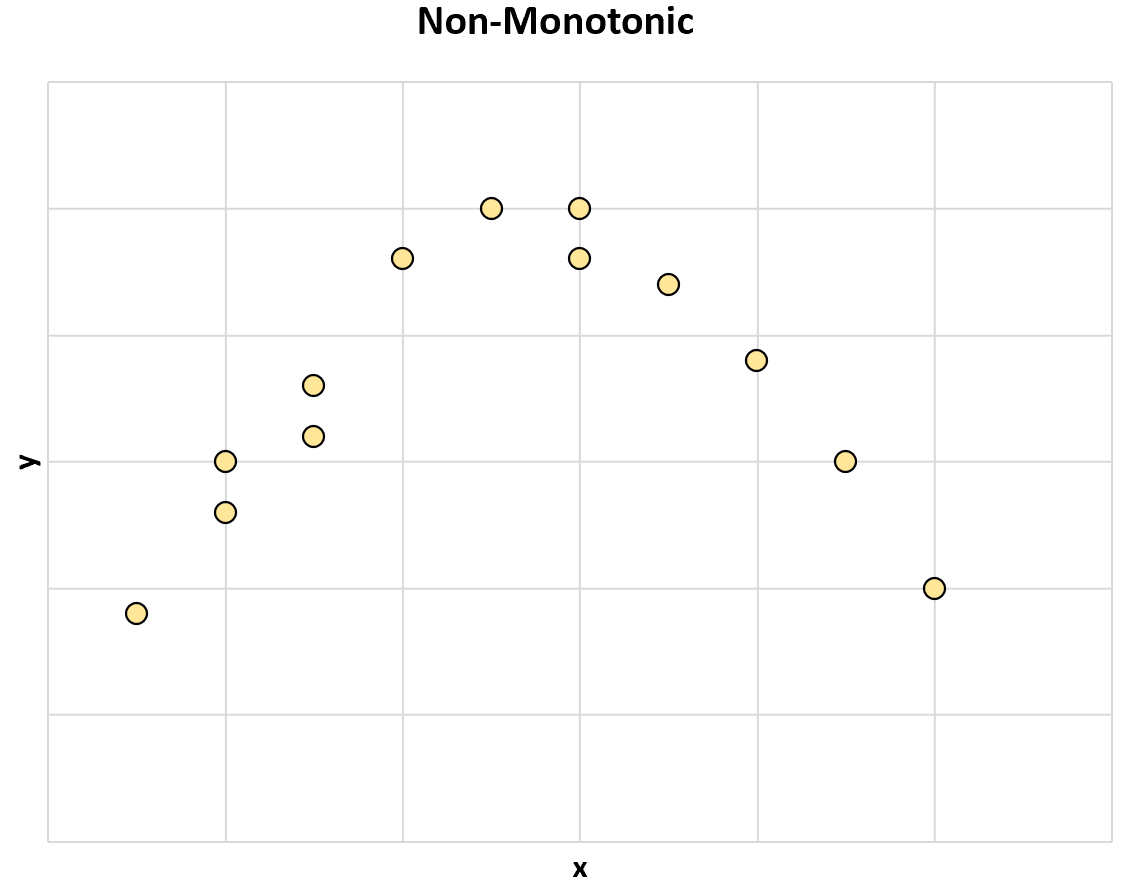
À mesure que la valeur de x augmente, la valeur de y augmente parfois , mais parfois la valeur de y diminue .
Strictement monotone ou non strictement monotone
On dit que deux variables ont une relation strictement monotone si les changements dans une variable sont toujours associés à un changement dans le même sens dans une autre variable.
Par exemple, le graphique suivant illustre une relation monotone strictement positive entre deux variables :
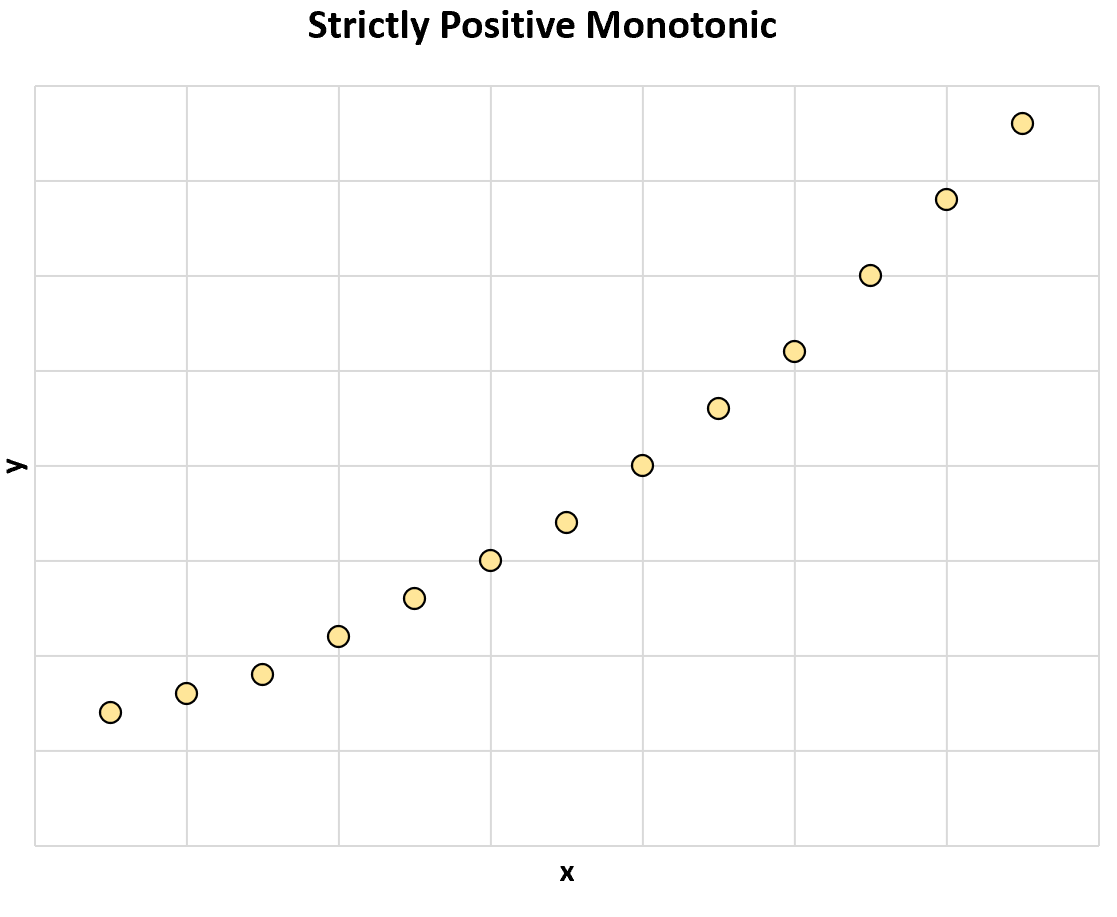
Lorsque la valeur de x augmente, la valeur de y augmente toujours .
Le graphique suivant illustre une relation monotone strictement négative entre deux variables :
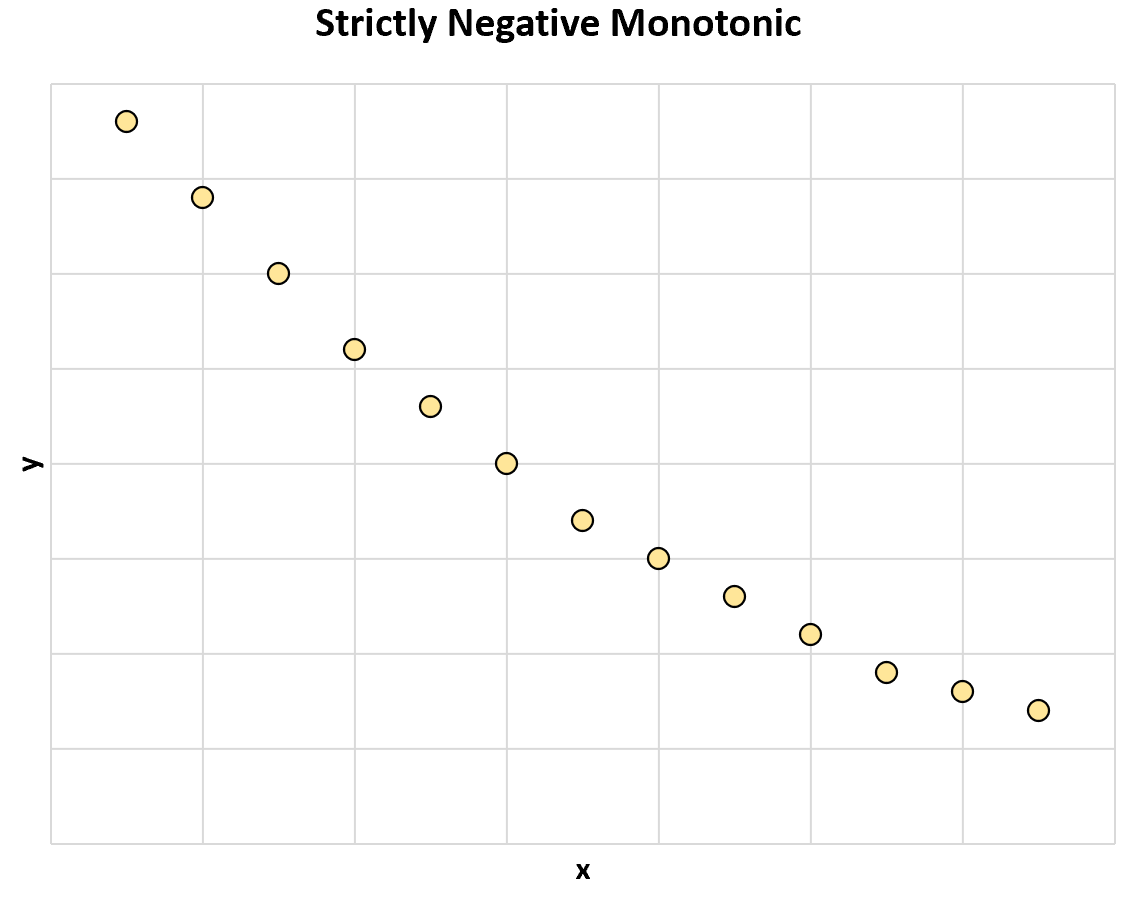
Lorsque la valeur de x augmente, la valeur de y diminue toujours .
Comment quantifier les relations monotones
La manière la plus courante de quantifier la relation entre deux variables consiste à utiliser le coefficient de corrélation de Pearson , qui mesure l’association linéaire entre deux variables.
Ce coefficient prend toujours une valeur comprise entre -1 et 1 où :
- -1 indique une corrélation linéaire parfaitement négative entre deux variables
- 0 indique aucune corrélation linéaire entre deux variables
- 1 indique une corrélation linéaire parfaitement positive entre deux variables
Plus le coefficient est proche de 1, plus la relation positive entre deux variables est forte. À l’inverse, plus le coefficient est proche de -1, plus la relation négative entre deux variables est forte.
Cependant, si la relation entre deux variables est monotone mais non linéaire (comme une relation exponentielle), alors c’est une bonne idée d’utiliser la corrélation de Spearman Rank , qui a été conçue pour bien gérer les relations monotones.
Quel que soit le type de coefficient de corrélation que vous calculez, c’est toujours une bonne idée de créer un nuage de points pour visualiser également la relation entre les variables.
