Qu’est-ce que Mallows ? Cp ? (Définition & Exemple)

Le Cp de Mallows est une métrique utilisée pour sélectionner le meilleur modèle de régression parmi plusieurs modèles différents.

Il est calculé comme suit :

Cp = RSS _p /S ² – N + 2(P+1)

où:

• RSS _p : La somme des carrés résiduelle pour un modèle avec p variables prédictives
• S ² : Le carré moyen résiduel du modèle (estimé par MSE)
• N : La taille de l’échantillon
• P : Le nombre de variables prédictives

Le Cp de Mallows est utilisé lorsque nous avons plusieurs variables prédictives potentielles que nous aimerions utiliser dans un modèle de régression et que nous souhaitons identifier le meilleur modèle qui utilise un sous-ensemble de ces variables prédictives.

Nous pouvons identifier le « meilleur » modèle de régression en identifiant le modèle avec la valeur Cp la plus basse inférieure à P+1, où P est le nombre de variables prédictives dans le modèle.

L’exemple suivant montre comment utiliser le Cp de Mallows pour sélectionner le meilleur modèle de régression parmi plusieurs modèles potentiels.

Exemple : Utilisation du Cp de Mallows pour sélectionner le meilleur modèle

Supposons qu’un professeur souhaite utiliser les heures étudiées, les examens préparatoires passés et la moyenne cumulative actuelle comme variables prédictives dans un modèle de régression pour prédire la note qu’un étudiant obtiendra à l’examen final.

Il ajuste sept modèles de régression différents et calcule la valeur du Cp de Mallows pour chaque modèle :

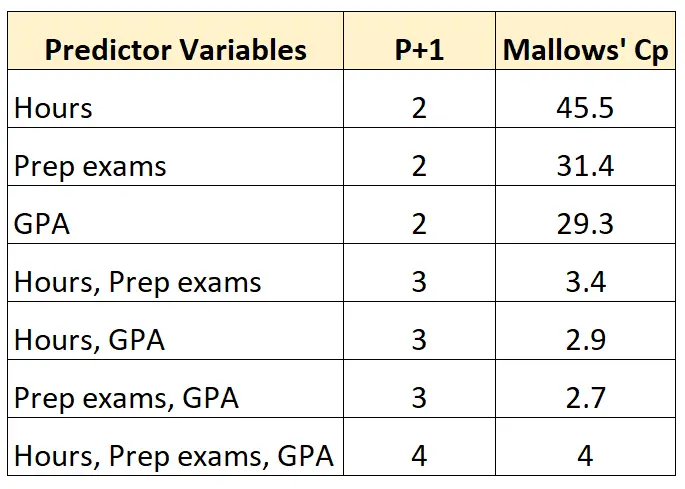
Si la valeur du Cp de Mallows est inférieure au nombre de coefficients du modèle (P+1), alors le modèle est dit sans biais.

Nous pouvons voir qu’il existe deux modèles impartiaux :

• Le modèle avec Hours et GPA comme variables prédictives (Mallows’ Cp = 2,9, P+1 = 3)
• Le modèle avec Prep Exams et GPA comme variables prédictives (Mallows’ Cp = 2,7, P+1 = 3)

Parmi ces deux modèles, le modèle qui utilise les examens préparatoires et la GPA comme variables prédictives a la valeur la plus faible pour le Cp de Mallows, ce qui nous indique que c’est le meilleur modèle qui entraîne le moins de biais.

Notes sur le Cp des mauves

Voici quelques points à garder à l’esprit concernant le Cp de Mallows :

• Les modèles qui ont une valeur Cp de Mallows proche de P+1 sont dits avoir un faible biais.
• Si chaque modèle potentiel a une valeur élevée pour le Cp de Mallows, cela indique que certaines variables prédictives importantes sont probablement absentes de chaque modèle.
• Si plusieurs modèles potentiels ont de faibles valeurs pour le Cp de Mallow, choisissez le modèle avec la valeur la plus faible comme meilleur modèle à utiliser.

Gardez également à l’esprit que le Cp de Mallows n’est qu’un moyen parmi d’autres de mesurer la qualité de l’ajustement d’un modèle de régression.

Une autre mesure couramment utilisée est le R-carré ajusté, qui nous indique la proportion de variance dans la variable de réponse qui peut être expliquée par les variables prédictives du modèle, ajustée en fonction du nombre de variables prédictives utilisées.

Pour décider quel modèle de régression est le meilleur parmi une liste de plusieurs modèles différents, c’est une bonne idée d’examiner à la fois le Cp de Mallows et le R carré ajusté.

Ressources additionnelles

Comment calculer le Cp de Mallows dans R
Comment calculer le R-carré ajusté en R