R vs R-Carré : quelle est la différence ?

Deux termes que les étudiants confondent souvent en statistiques sont R et R-carré , souvent écrits R ² .

Dans le cadre d’ une régression linéaire simple :

• R : La corrélation entre la variable prédictive, x, et la variable de réponse, y.
• R ² : Proportion de la variance de la variable de réponse qui peut être expliquée par la variable prédictive dans le modèle de régression.

Et dans le cadre d’ une régression linéaire multiple :

• R : La corrélation entre les valeurs observées de la variable de réponse et les valeurs prédites de la variable de réponse faites par le modèle.
• R ² : Proportion de la variance de la variable de réponse qui peut être expliquée par les variables prédictives du modèle de régression.

Notez que la valeur de R ² est comprise entre 0 et 1. Plus la valeur est proche de 1, plus la relation entre la ou les variables prédictives et la variable de réponse est forte.

Les exemples suivants montrent comment interpréter les valeurs R et R au carré dans les modèles de régression linéaire simple et de régression linéaire multiple.

Exemple 1 : Régression linéaire simple

Supposons que nous disposions de l’ensemble de données suivant qui montre les heures étudiées et les résultats aux examens obtenus par 12 étudiants dans un certain cours de mathématiques :

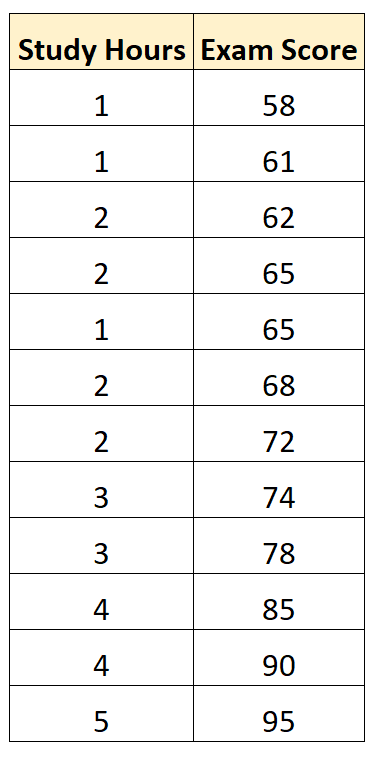
À l’aide de logiciels statistiques (comme Excel, R, Python, SPSS, etc.), nous pouvons ajuster un modèle de régression linéaire simple en utilisant les « heures d’étude » comme variable prédictive et la « note d’examen » comme variable de réponse .

Nous pouvons trouver la sortie suivante pour ce modèle :

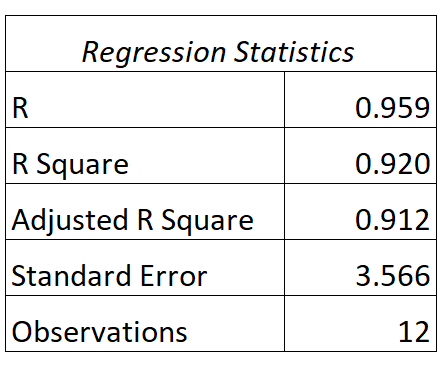
Voici comment interpréter les valeurs R et R au carré de ce modèle :

• R : La corrélation entre les heures étudiées et la note à l’examen est de 0,959 .
• R ² : Le R au carré pour ce modèle de régression est de 0,920 . Cela nous indique que 92,0 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées.

Notez également que la valeur R ² est simplement égale à la valeur R, au carré :

^R2 = R * R = 0,959 * 0,959 = 0,920

Exemple 2 : Régression linéaire multiple

Supposons que nous disposions de l’ensemble de données suivant qui montre les heures étudiées, la note actuelle de l’étudiant et la note d’examen obtenue par 12 étudiants dans un certain cours de mathématiques :

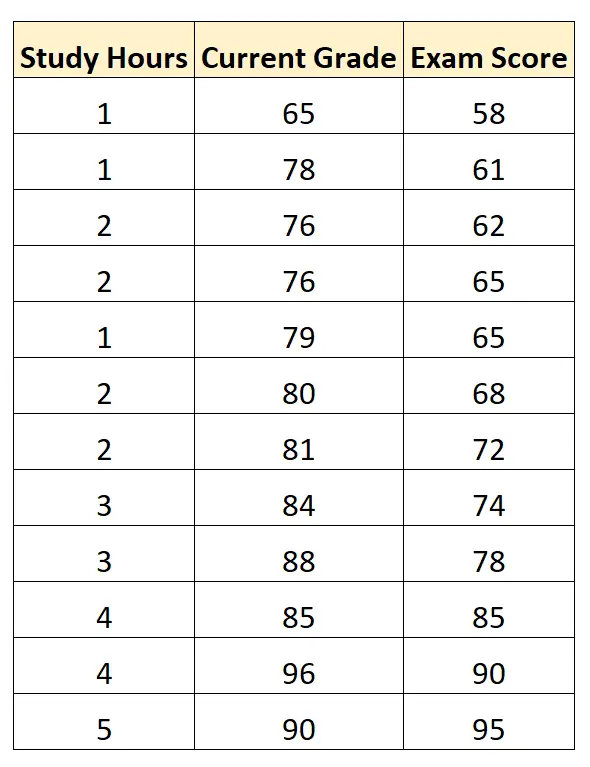
À l’aide d’un logiciel statistique, nous pouvons ajuster un modèle de régression linéaire multiple en utilisant les « heures d’étude » et la « note actuelle » comme variables prédictives et la « note à l’examen » comme variable de réponse.

Nous pouvons trouver la sortie suivante pour ce modèle :

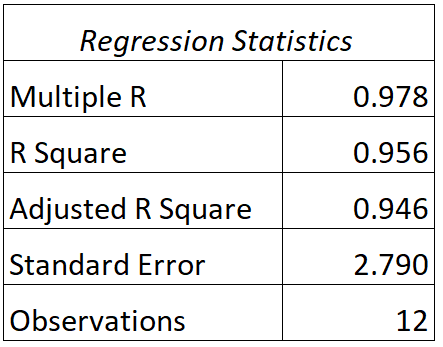
Voici comment interpréter les valeurs R et R au carré de ce modèle :

• R : La corrélation entre les résultats réels des examens et les résultats prévus aux examens effectués par le modèle est de 0,978 .
• R ² : Le R au carré pour ce modèle de régression est de 0,956 . Cela nous indique que 95,6 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées et la note actuelle de l’étudiant dans la classe.

Notez également que la valeur R ² est simplement égale à la valeur R, au carré :

^R2 = R * R = 0,978 * 0,978 = 0,956

Ressources additionnelles

Qu’est-ce qu’une bonne valeur R au carré ?
Un guide doux sur la somme des carrés : SST, SSR, SSE