ANOVA vs régression : quelle est la différence ?
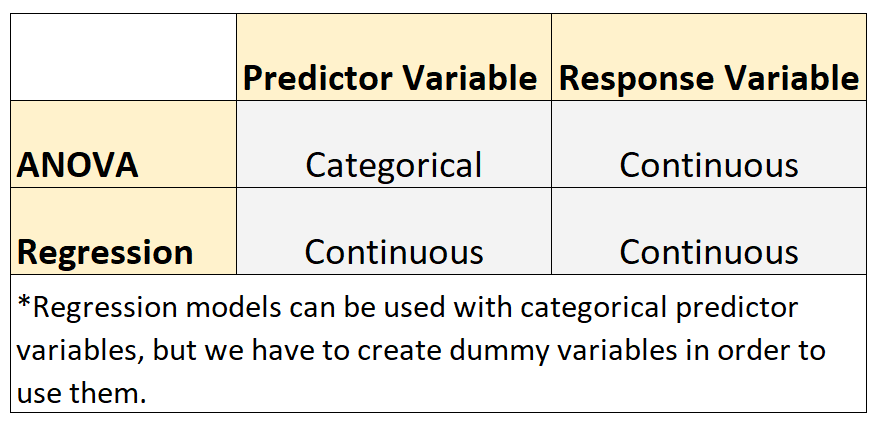
Deux modèles couramment utilisés en statistique sont les modèles ANOVA et de régression.
Ces deux types de modèles partagent la similitude suivante :
- La variable de réponse dans chaque modèle est continue. Des exemples de variables continues incluent le poids, la taille, la longueur, la largeur, le temps, l’âge, etc.
Cependant, ces deux types de modèles partagent la différence suivante :
- Les modèles ANOVA sont utilisés lorsque les variables prédictives sont catégorielles. Des exemples de variables catégorielles incluent le niveau d’éducation, la couleur des yeux, l’état civil, etc.
- Les modèles de régression sont utilisés lorsque les variables prédictives sont continues.*
*Les modèles de régression peuvent être utilisés avec des variables prédictives catégorielles, mais nous devons créer des variables fictives pour pouvoir les utiliser.
Les exemples suivants montrent quand utiliser les modèles ANOVA ou de régression dans la pratique.
Exemple 1 : modèle ANOVA préféré
Supposons qu’un biologiste veuille comprendre si quatre engrais différents conduisent ou non à la même croissance moyenne des plantes (en pouces) sur une période d’un mois. Pour tester cela, elle applique chaque engrais sur 20 plantes et enregistre la croissance de chaque plante après un mois.
Dans ce scénario, le biologiste doit utiliser un modèle ANOVA unidirectionnel pour analyser les différences entre les engrais, car il existe une variable prédictive et elle est catégorique.
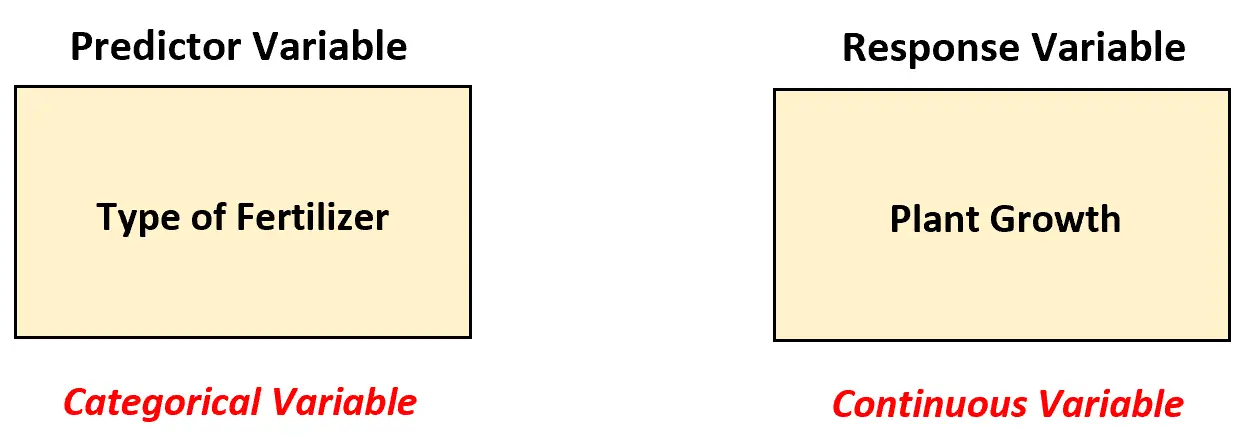
En d’autres termes, les valeurs de la variable prédictive peuvent être classées dans les « catégories » suivantes :
- Engrais 1
- Engrais 2
- Engrais 3
- Engrais 4
Une ANOVA unidirectionnelle indiquera au biologiste si la croissance moyenne des plantes est égale ou non entre les quatre engrais différents.
Exemple 2 : modèle de régression préféré
Supposons qu’un agent immobilier souhaite comprendre la relation entre la superficie en pieds carrés et le prix de l’immobilier. Pour analyser cette relation, il collecte des données sur la superficie en pieds carrés et le prix de 200 maisons dans une ville particulière.
Dans ce scénario, l’agent immobilier doit utiliser un modèle de régression linéaire simple pour analyser la relation entre ces deux variables, car la variable prédictive (superficie en pieds carrés) est continue.
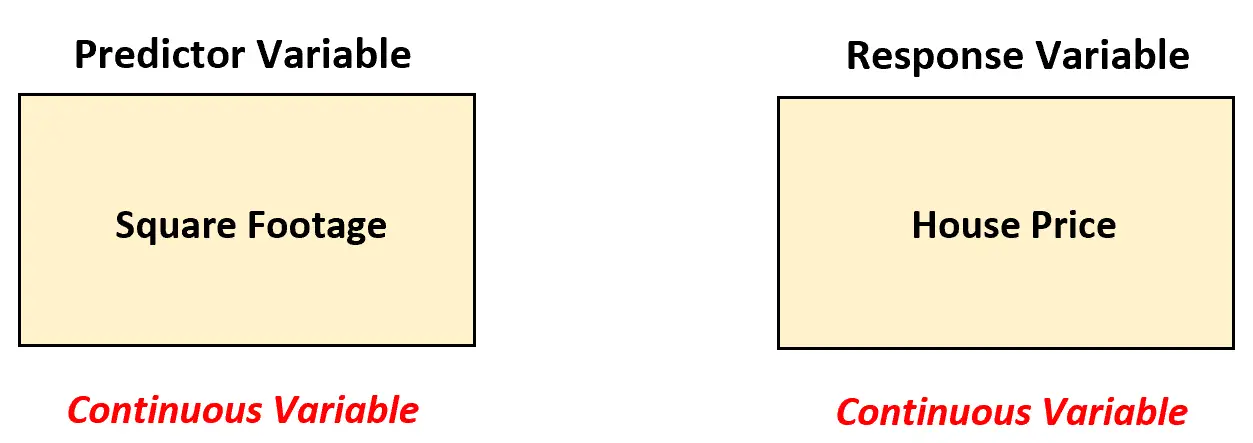
À l’aide d’une régression linéaire simple, l’agent immobilier peut adapter le modèle de régression suivant :
Prix de l’immobilier = β 0 + β 1 (superficie carrée)
La valeur de β 1 représentera la variation moyenne du prix de l’immobilier associée à chaque pied carré supplémentaire.
Cela permettra à l’agent immobilier de quantifier la relation entre la superficie en pieds carrés et le prix de l’immobilier.
Exemple 3 : modèle de régression avec variables factices préférées
Supposons qu’un agent immobilier souhaite comprendre la relation entre les variables prédictives « superficie » et « type de maison » (unifamiliale, appartement, maison en rangée) avec la variable de réponse du prix de l’immobilier.
Dans ce scénario, l’agent immobilier peut utiliser la régression linéaire multiple en convertissant le « type de maison » en une variable muette puisqu’il s’agit actuellement d’une variable catégorielle.
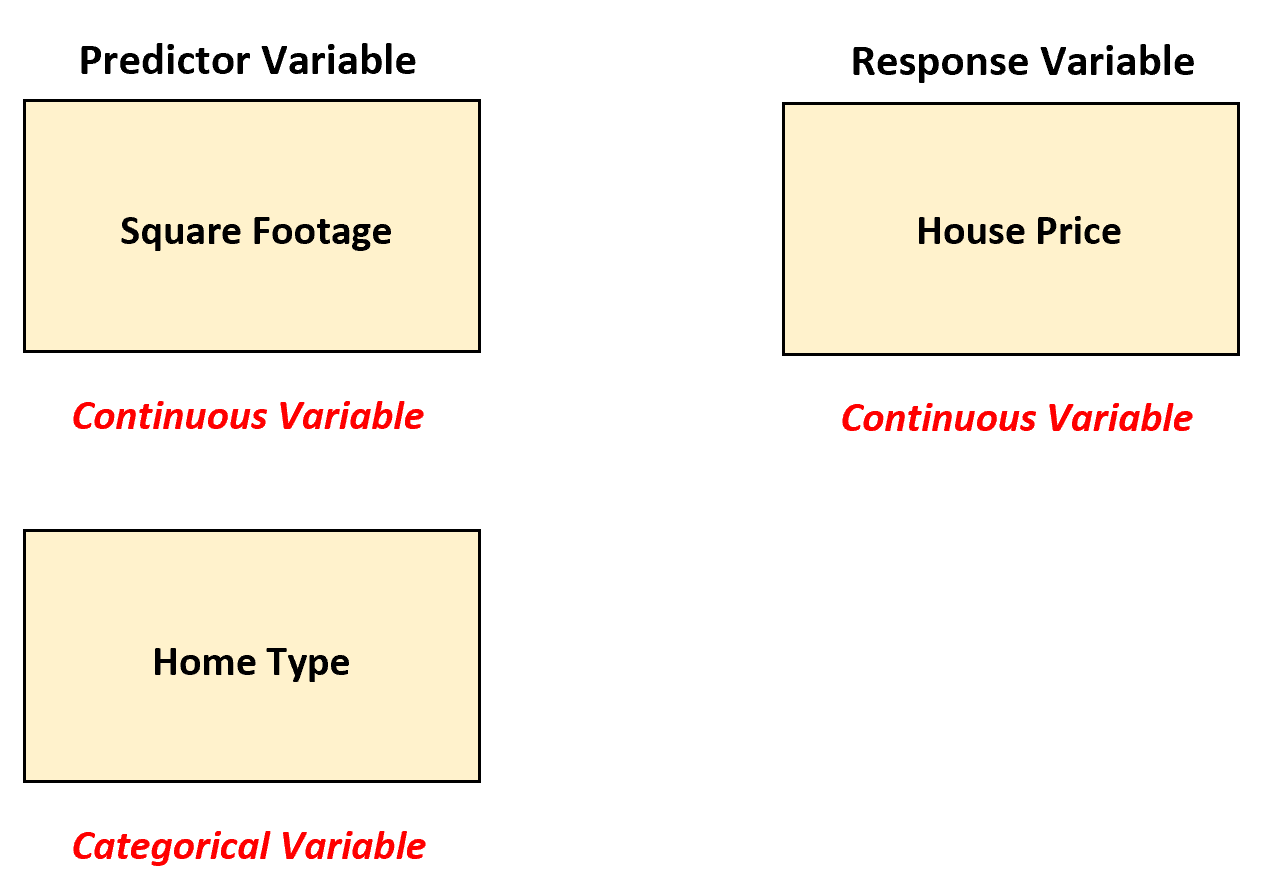
L’agent immobilier peut alors ajuster le modèle de régression linéaire multiple suivant :
Prix de l’immobilier = β 0 + β 1 (superficie carrée) + β 2 (unifamiliale) + β 3 (appartement)
Voici comment nous interpréterions les coefficients du modèle :
- β 1 : La variation moyenne du prix de l’immobilier associée à un pied carré supplémentaire.
- β 2 : La différence moyenne de prix entre une maison unifamiliale et une maison en rangée, en supposant que la superficie en pieds carrés reste constante.
- β 3 : Différence moyenne de prix entre une maison unifamiliale et un appartement, en supposant une superficie constante.
Consultez les didacticiels suivants pour voir comment créer des variables factices dans différents logiciels statistiques :
Ressources additionnelles
Les didacticiels suivants offrent une introduction approfondie aux modèles ANOVA :
Les didacticiels suivants offrent une introduction approfondie aux modèles de régression linéaire :
