Comment appliquer le théorème central limite sur la calculatrice TI-84
Le théorème central limite stipule que la distribution d’échantillonnage d’une moyenne d’échantillon est approximativement normale si la taille de l’échantillon est suffisamment grande, même si la distribution de la population n’est pas normale.
Le théorème central limite indique également que la distribution d’échantillonnage aura les propriétés suivantes :
1. La moyenne de la distribution d’échantillonnage sera égale à la moyenne de la distribution de la population :
x = µ
2. L’écart type de la distribution d’échantillonnage sera égal à l’écart type de la population divisé par la taille de l’échantillon :
s = σ / √n
Pour trouver les probabilités liées à la moyenne de l’échantillon sur une calculatrice TI-84, nous pouvons utiliser la fonction normalcdf() avec la syntaxe suivante :
normalcdf(lower value, upper value, x, s/√n)
où:
- x : moyenne de l’échantillon
- s : écart type de l’échantillon
- n : taille de l’échantillon
Pour accéder à cette fonction sur une calculatrice TI-84, appuyez simplement sur 2nd puis appuyez sur VARS puis faites défiler jusqu’à normalcdf ( et appuyez sur ENTER .
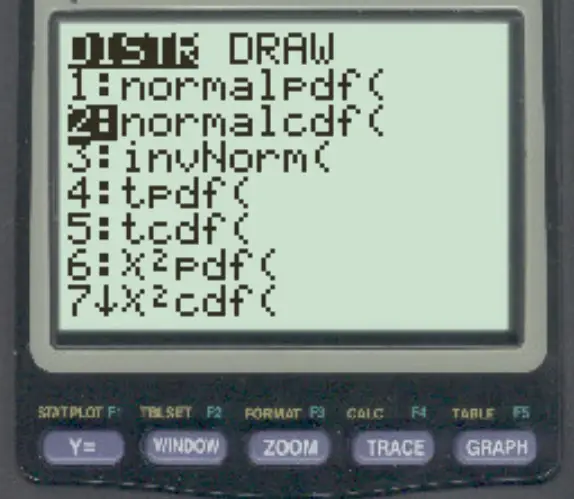
Les exemples suivants montrent comment utiliser cette fonction dans la pratique.
Exemple 1 : Trouver la probabilité entre deux valeurs
Une distribution a une moyenne de 70 et un écart type de 7. Si nous sélectionnons un échantillon aléatoire de taille n = 35, trouvez la probabilité que la moyenne de l’échantillon soit comprise entre 68 et 72.
Nous pouvons utiliser la syntaxe suivante sur la TI-84 :
normalcdf(68, 72, 70, 7/√35)
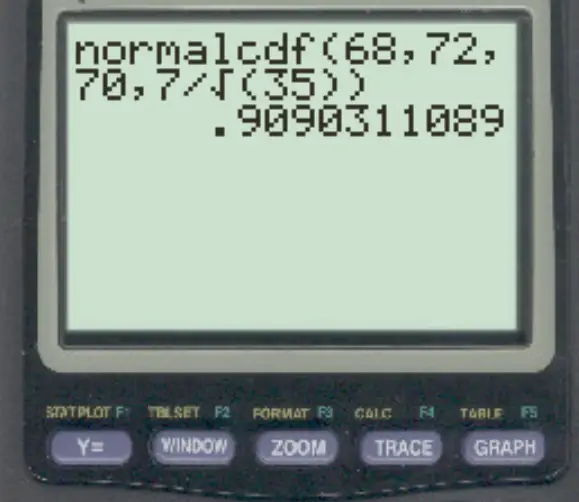
La probabilité que la moyenne de l’échantillon soit comprise entre 68 et 72 est de 0,909 .
Exemple 2 : Trouver une probabilité supérieure à une valeur
Une distribution a une moyenne de 50 et un écart type de 4. Si nous sélectionnons un échantillon aléatoire de taille n = 30, trouvez la probabilité que la moyenne de l’échantillon soit supérieure à 48.
Nous pouvons utiliser la syntaxe suivante sur la TI-84 :
normalcdf(48, E99, 50, 4/√30)
Remarque : Vous pouvez accéder au symbole « E » en appuyant sur 2 , puis en appuyant sur le bouton , .
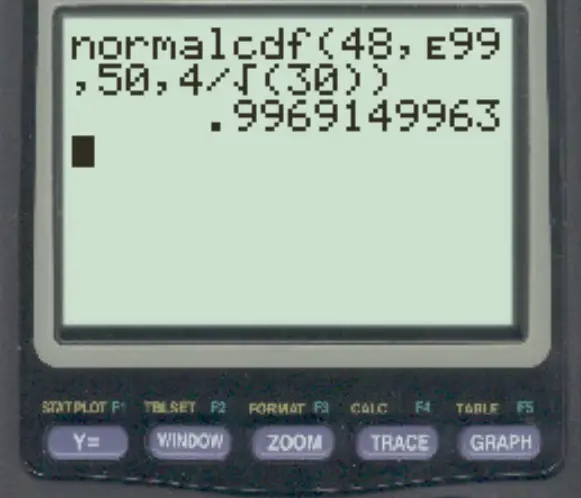
La probabilité que la moyenne de l’échantillon soit supérieure à 48 est de 0,9969 .
Exemple 3 : Trouver une probabilité inférieure à une valeur
Une distribution a une moyenne de 20 et un écart type de 3. Si nous sélectionnons un échantillon aléatoire de taille n = 40, trouvez la probabilité que la moyenne de l’échantillon soit inférieure à 19.
Nous pouvons utiliser la syntaxe suivante sur la TI-84 :
normalcdf(-E99, 19, 20, 3/√40)
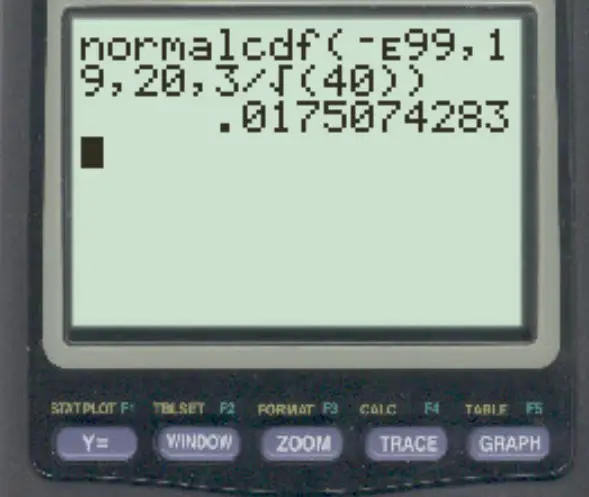
La probabilité que la moyenne de l’échantillon soit inférieure à 19 est de 0,0175 .
Ressources additionnelles
Une introduction au théorème central limite
Calculateur du théorème central limite
Comment appliquer le théorème central limite dans Excel
Théorème central limite : les quatre conditions à remplir
