Comment créer un tracé résiduel à la main

Un tracé des résidus est un type de tracé qui affiche les valeurs d’une variable prédictive dans un modèle de régression le long de l’axe des x et les valeurs des résidus le long de l’axe des y.

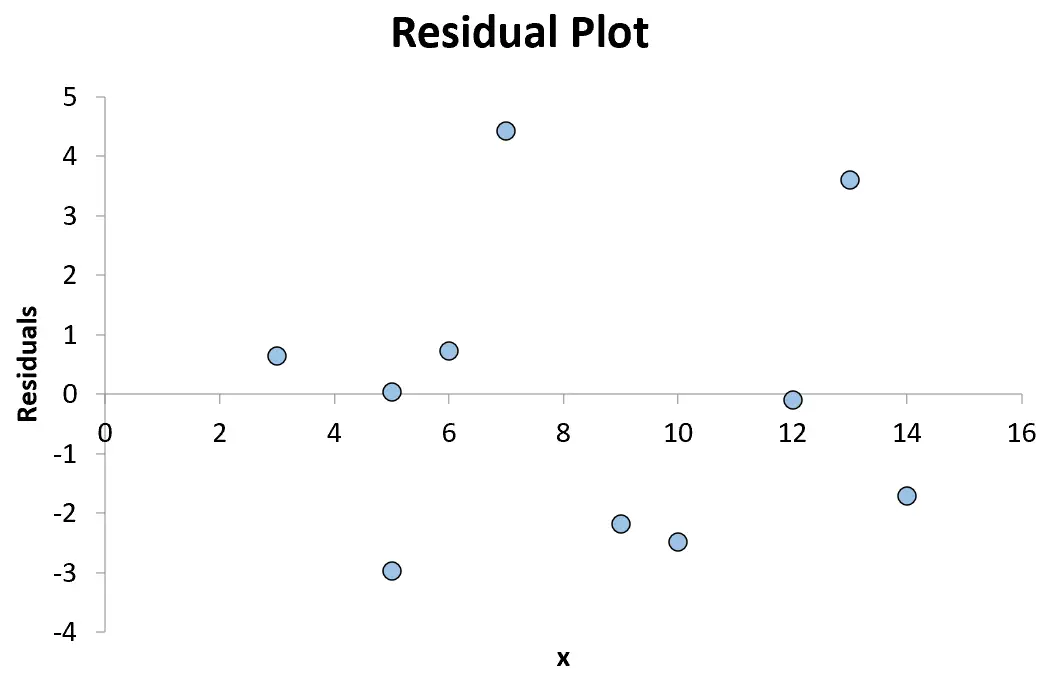
Ce graphique est utilisé pour évaluer si les résidus d’un modèle de régression sont normalement distribués et s’ils présentent ou non une hétéroscédasticité .

L’exemple suivant, étape par étape, montre comment créer manuellement un tracé des résidus pour un modèle de régression.

Étape 1 : Trouver les valeurs prédites

Supposons que nous souhaitions adapter un modèle de régression à l’ensemble de données suivant :

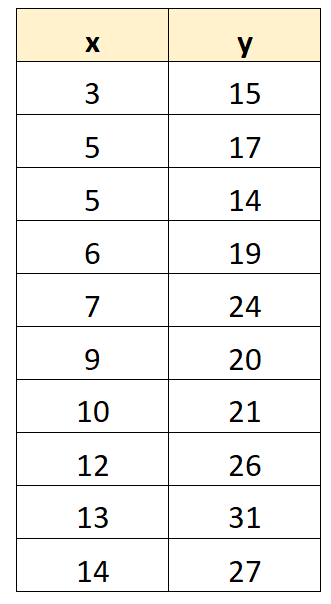
En utilisant des logiciels statistiques (comme Excel, R, Python, SPSS, etc.), nous pouvons constater que le modèle de régression ajusté est :

y = 10,4486 + 1,3037(x)

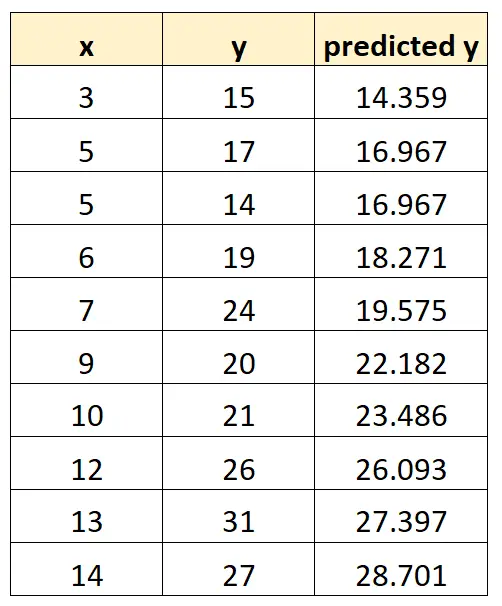
Nous pouvons ensuite utiliser ce modèle pour prédire la valeur de y, en fonction de la valeur de x. Par exemple, si x = 3, alors nous prédisons que y sera :

y = 10,4486 + 1,3037(3) = 14,359

Nous pouvons répéter ce processus pour chaque observation de notre ensemble de données :

Étape 2 : Trouver les résidus

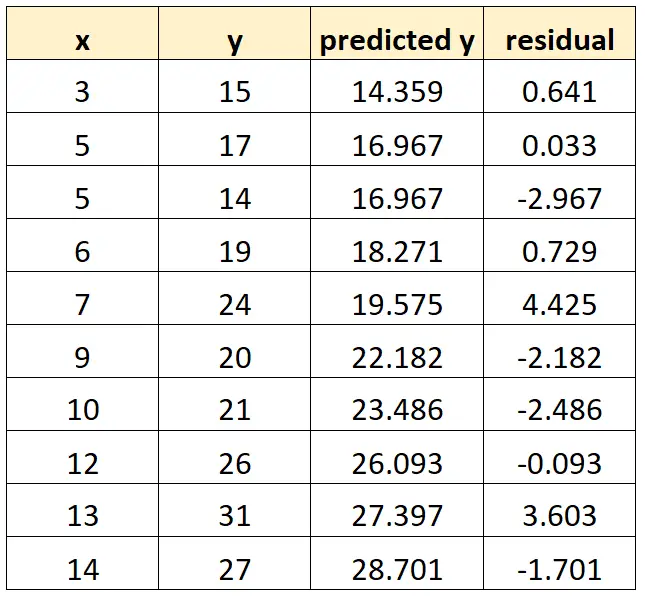
Un résidu pour une observation donnée dans notre ensemble de données est calculé comme suit :

Résidu = valeur observée – valeur prédite

Par exemple, le résidu de la première observation serait calculé comme suit :

Résiduel = 15 – 14,359 = 0,641

Nous pouvons répéter ce processus pour chaque observation de notre ensemble de données :

Étape 3 : Créer le tracé résiduel

Enfin, nous pouvons créer un tracé résiduel en plaçant les valeurs x le long de l’axe des x et les valeurs résiduelles le long de l’axe des y.

Par exemple, le premier point que nous placerons dans notre graphique est (3, 0,641)

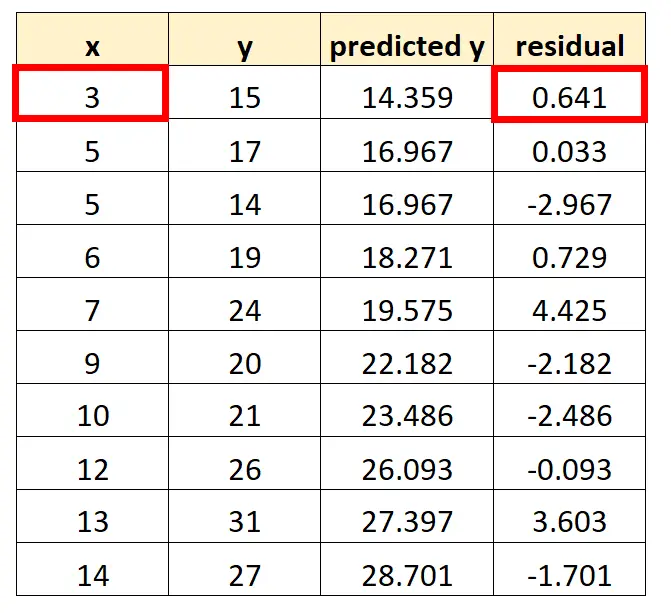
Le prochain point que nous placerons dans notre graphique est (5, 0,033)

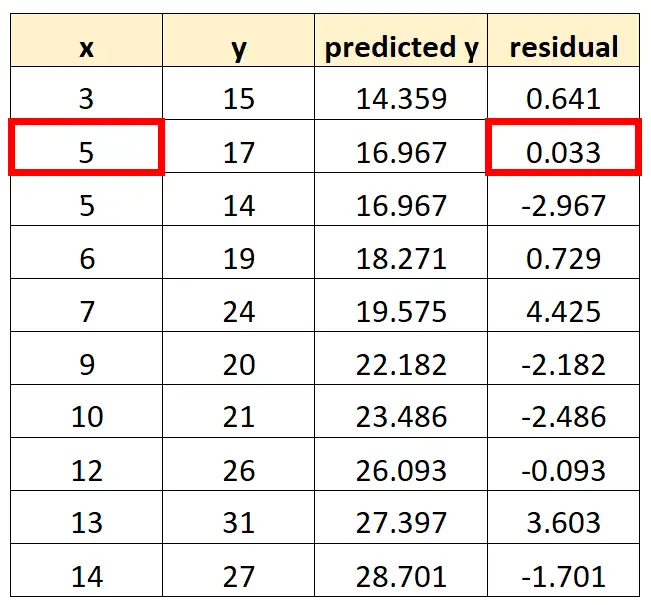
Nous continuerons jusqu’à ce que nous ayons placé les 10 combinaisons par paires de valeurs x et de valeurs résiduelles dans le tracé :

Tout point au-dessus de zéro dans le graphique représente un résidu positif. Cela signifie que la valeur observée pour y est supérieure à la valeur prédite par le modèle de régression.

Tout point inférieur à zéro représente un résidu négatif. Cela signifie que la valeur observée pour y est inférieure à la valeur prédite par le modèle de régression.

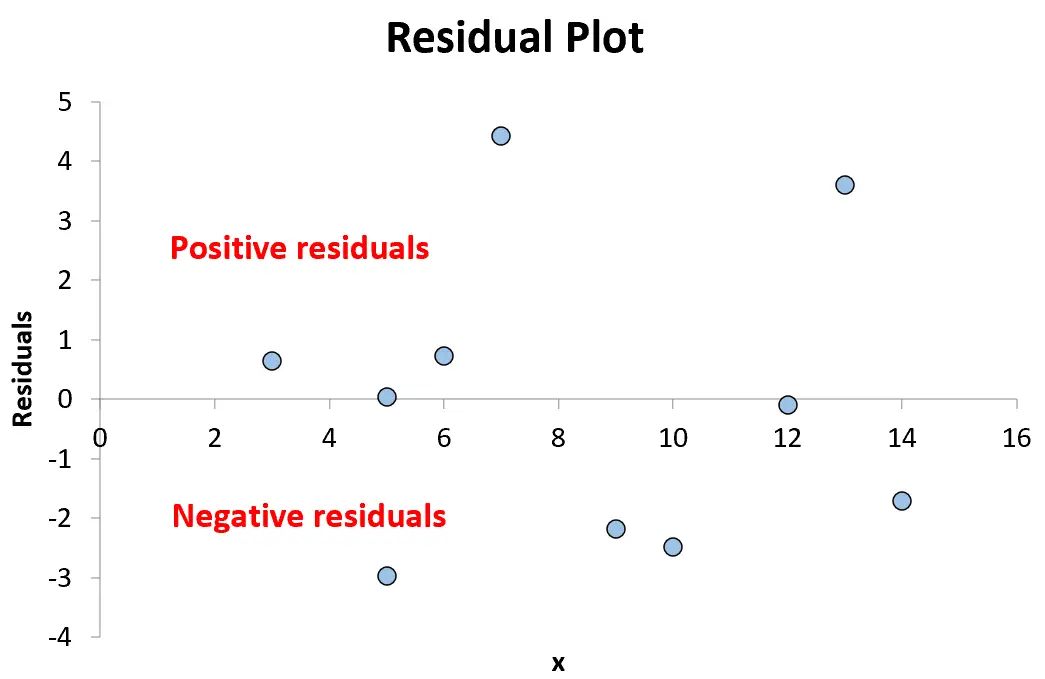
Étant donné que les points du graphique sont dispersés de manière aléatoire autour d’une valeur résiduelle de 0 sans motif clair, cela indique que la relation entre x et y est linéaire et qu’il est approprié d’utiliser un modèle de régression linéaire.

Et comme les résidus n’augmentent ou ne diminuent pas systématiquement à mesure que la variable prédictive augmente, cela signifie que l’hétéroscédasticité n’est pas un problème avec ce modèle de régression.

Ressources additionnelles

Les didacticiels suivants expliquent comment créer des tracés de résidus à l’aide de différents logiciels statistiques :

Comment créer un tracé résiduel sur une calculatrice TI-84
Comment créer un tracé résiduel dans Excel
Comment créer un tracé résiduel dans R
Comment créer un tracé résiduel en Python