Comment effectuer un test t apparié à la main
Un test t pour échantillons appariés est utilisé pour comparer les moyennes de deux échantillons lorsque chaque observation dans un échantillon peut être associée à une observation dans l’autre échantillon.
L’exemple étape par étape suivant montre comment effectuer un test t pour échantillons appariés pour déterminer si les moyennes de la population sont égales entre les deux groupes suivants :
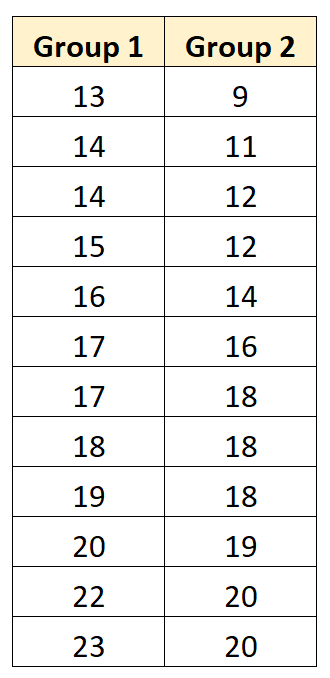
Étape 1 : Calculer la statistique du test
La statistique de test d’un test t apparié est calculée comme suit :
t = x diff / (s diff /√ n )
où:
- x diff : exemple de moyenne des différences
- s : exemple d’écart type des différences
- n : taille de l’échantillon (c’est-à-dire nombre de paires)
Nous calculerons la moyenne des différences entre les deux groupes et l’écart type des différences entre les deux groupes :
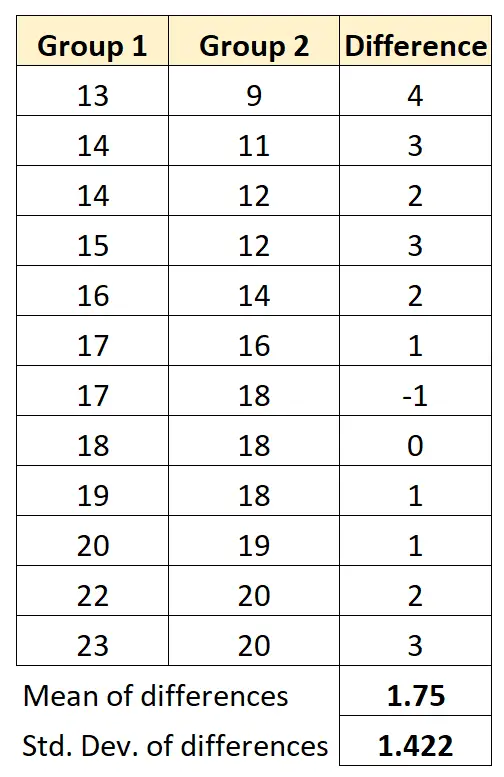
Ainsi, notre statistique de test peut être calculée comme suit :
- t = x diff / (s diff /√ n )
- t = 1,75 / (1,422/√ 12 )
- t = 4,26
Étape 2 : Calculer la valeur critique
Ensuite, nous devons trouver la valeur critique à laquelle comparer nos statistiques de test.
Pour cet exemple, nous utiliserons un test bilatéral avec α = 0,05 et df = n-1 degrés de liberté.
D’après le tableau de distribution t , la valeur critique qui correspond à ces valeurs est 2,201 :
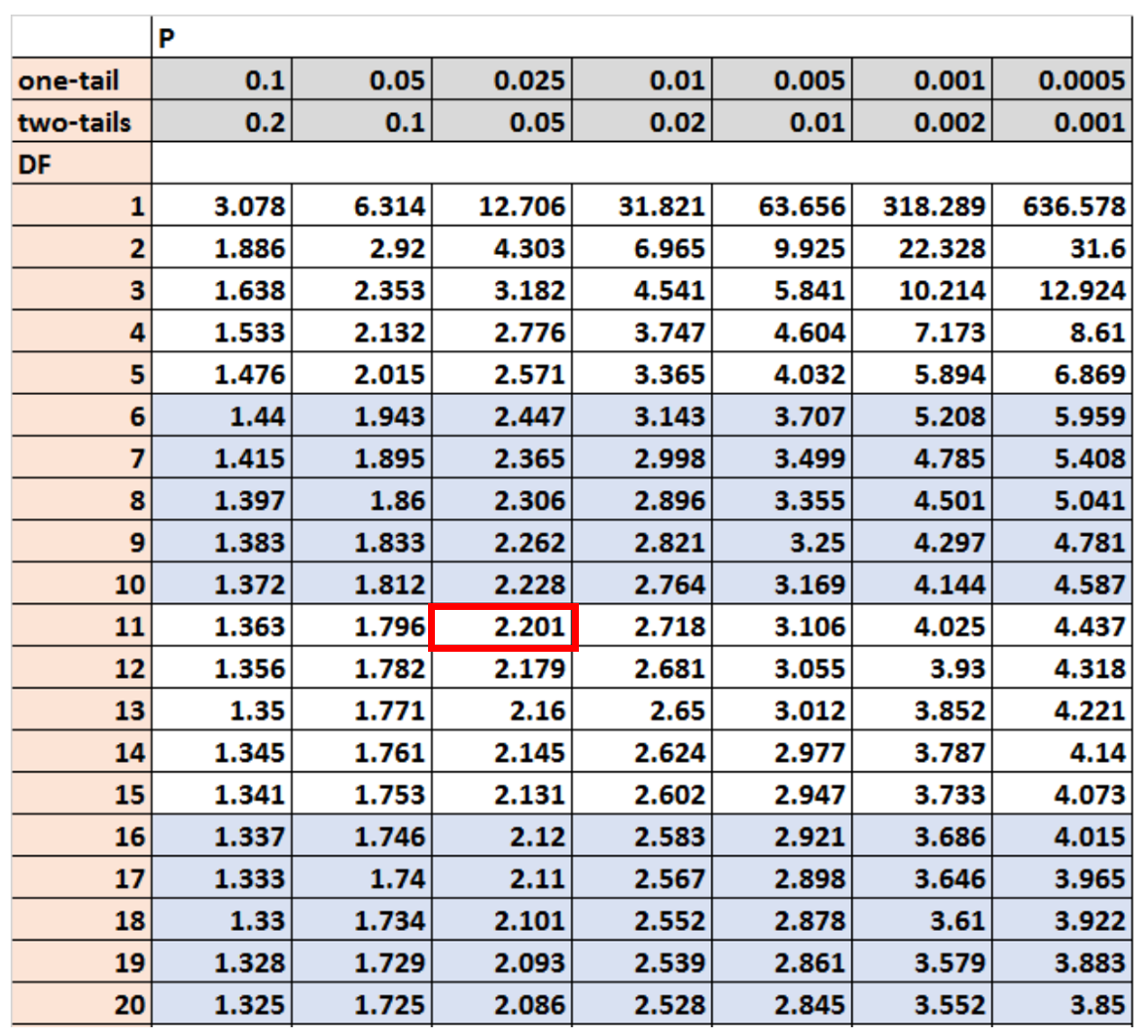
Étape 3 : Rejeter ou échouer à rejeter l’hypothèse nulle
Notre test t pour échantillons appariés utilise l’hypothèse nulle et alternative suivante :
- H 0 : μ 1 = μ 2 (les deux moyennes de population sont égales)
- H A : μ 1 ≠ μ 2 (les deux moyennes de population ne sont pas égales)
Puisque la valeur absolue de notre statistique de test ( 4.26 ) est supérieure à la valeur critique trouvée dans la table t ( 2.201 ), nous rejetons l’hypothèse nulle.
Cela signifie que nous disposons de suffisamment de preuves pour affirmer que la moyenne entre les deux groupes n’est pas égale.
Bonus : n’hésitez pas à utiliser le calculateur de test t pour échantillons appariés pour confirmer vos résultats.
