Comment utiliser geometpdf() et geometcdf() sur une calculatrice TI-84
La distribution géométrique décrit la probabilité de connaître un certain nombre d’échecs avant de connaître le premier succès dans une série d’essais présentant les caractéristiques suivantes :
- Il n’y a que deux résultats possibles : le succès ou l’échec.
- La probabilité de succès est la même dans chaque essai.
Si une variable aléatoire X suit une distribution géométrique, alors la probabilité de connaître k échecs avant de connaître le premier succès peut être trouvée par la formule suivante :
P(X=k) = (1-p) kp
où:
- k : nombre d’échecs avant le premier succès
- p : probabilité de succès à chaque essai
La probabilité cumulée que nous subissions k échecs ou moins jusqu’au premier succès peut être trouvée en utilisant la formule suivante :
P(X≤k) = 1 – (1-p) k+1
Pour calculer les probabilités liées à la distribution géométrique sur une calculatrice TI-84, on peut utiliser les fonctions suivantes :
- geometpdf (probabilités, essais)
- geometcdf(probabilité, essais)
Les exemples suivants montrent comment utiliser chacune de ces fonctions dans la pratique.
Exemple 1 : Comment utiliser geometpdf()
Supposons qu’un chercheur attende à l’extérieur d’une bibliothèque pour demander aux gens s’ils soutiennent une certaine loi. La probabilité qu’une personne donnée soutienne la loi est p = 0,2. Quelle est la probabilité que la quatrième personne à qui le chercheur s’adresse soit la première à soutenir la loi ?
Pour répondre à cette question, nous pouvons utiliser la fonction geometpdf() .
Appuyez sur 2ème puis appuyez sur VARS . Faites défiler jusqu’à geometpdf() et appuyez sur ENTER .
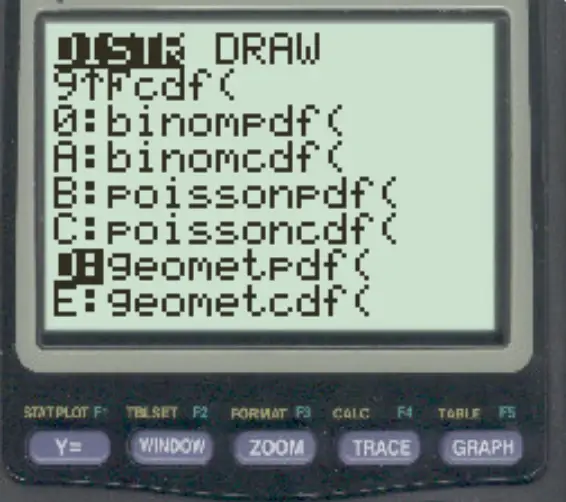
Tapez ensuite les valeurs suivantes et appuyez sur ENTER .
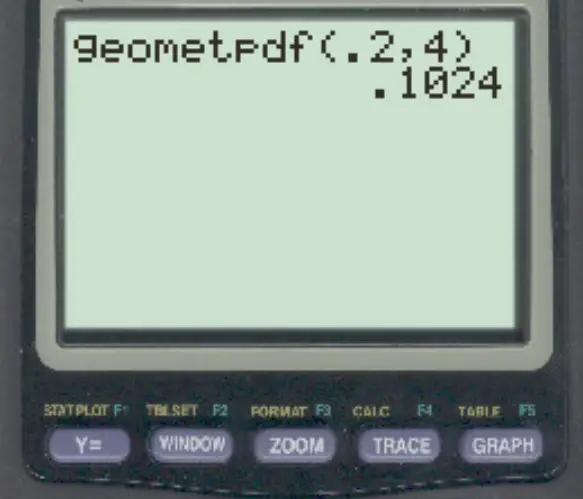
La probabilité que la quatrième personne à qui le chercheur s’adresse soit la première à soutenir la loi est de 0,1024 .
Exemple 2 : Comment utiliser geometcdf()
Supposons que l’on sache que 4 % des personnes qui rendent visite à un certain banquier le font pour déclarer faillite. Quelle est la probabilité que le banquier rencontre moins de 9 personnes avant de rencontrer quelqu’un qui déclare faillite ?
Pour répondre à cette question, nous pouvons utiliser la fonction geometcdf() .
Appuyez sur 2ème puis appuyez sur VARS . Faites défiler jusqu’à geometcdf() et appuyez sur ENTER .
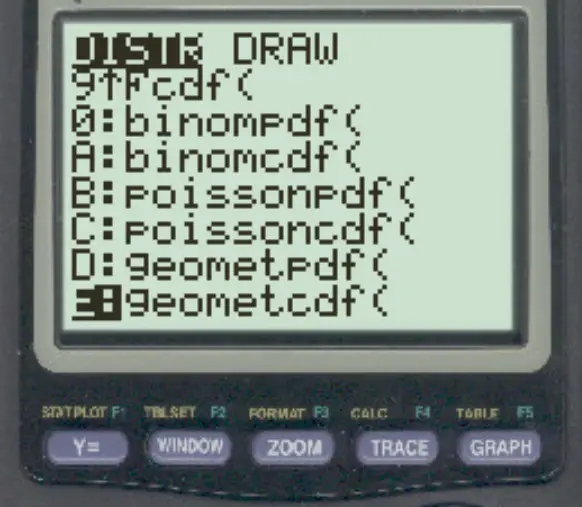
Tapez ensuite les valeurs suivantes et appuyez sur ENTER .
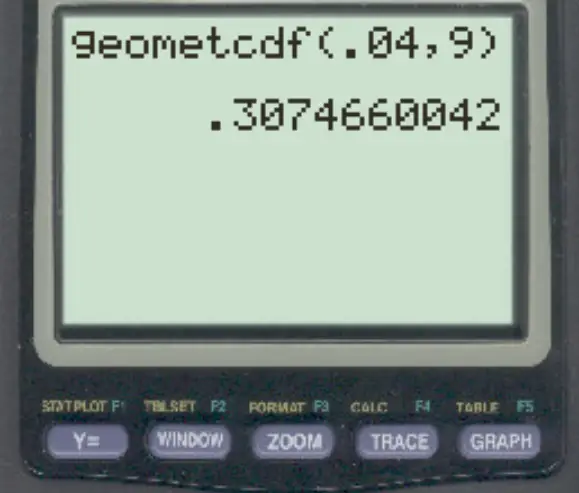
La probabilité que le banquier rencontre moins de 9 personnes avant de rencontrer quelqu’un qui déclare faillite est de 0,307466 .
Bonus : N’hésitez pas à utiliser ce calculateur de distribution géométrique en ligne pour confirmer vos résultats.
Ressources additionnelles
Comment calculer les probabilités normales sur une calculatrice TI-84
Comment calculer les probabilités binomiales sur une calculatrice TI-84
Comment calculer les probabilités de Poisson sur une calculatrice TI-84
