Qu’est-ce que l’écart résiduel ? (Définition & #038; Exemple)

La variance résiduelle (parfois appelée « variance inexpliquée ») fait référence à la variance d’un modèle qui ne peut pas être expliquée par les variables du modèle.

Plus la variance résiduelle d’un modèle est élevée, moins le modèle est capable d’expliquer la variation des données.

La variance résiduelle apparaît dans les résultats de deux modèles statistiques différents :

1. ANOVA : utilisée pour comparer les moyennes de trois groupes indépendants ou plus.

2. Régression : utilisée pour quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Les exemples suivants montrent comment interpréter la variance résiduelle dans chacune de ces méthodes.

Variance résiduelle dans les modèles ANOVA

Chaque fois que nous ajustons un modèle ANOVA (« analyse de variance »), nous nous retrouvons avec un tableau ANOVA qui ressemble au suivant :

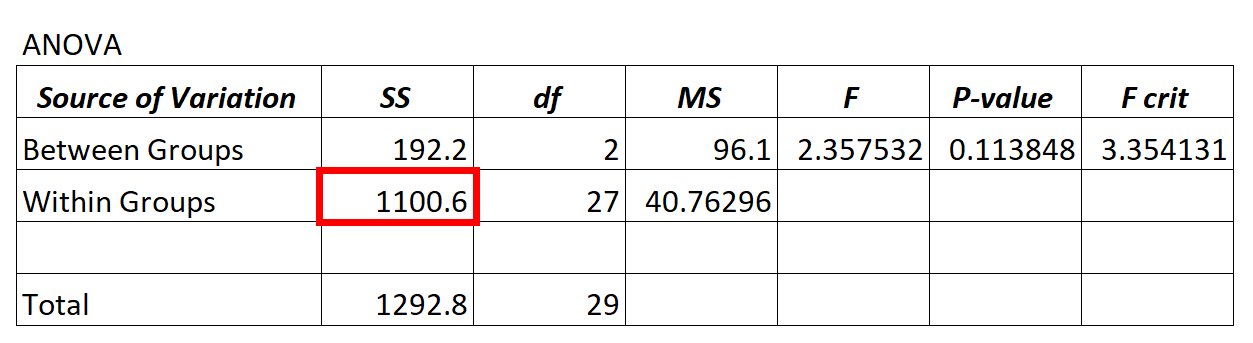
La valeur de la variance résiduelle du modèle ANOVA se trouve dans la colonne SS (« somme des carrés ») pour la variation intra-groupes .

Cette valeur est également appelée « somme des erreurs quadratiques » et est calculée à l’aide de la formule suivante :

Σ(X _ij – X _j ) ²

où:

• Σ : un symbole grec qui signifie « somme »
• X _ij : la ^ième observation du groupe j
• X _j : la moyenne du groupe j

Dans le modèle ANOVA ci-dessus, nous voyons que la variance résiduelle est de 1 100,6.

Pour déterminer si cette variance résiduelle est « élevée », nous pouvons calculer la somme moyenne des carrés pour au sein des groupes et la somme moyenne des carrés pour entre les groupes et trouver le rapport entre les deux, ce qui donne la valeur F globale dans le tableau ANOVA.

• F = MS _entre / MS _dans
• F = 96,1 / 40,76296
• F = 2,357

La valeur F dans le tableau ANOVA ci-dessus est de 2,357 et la valeur p correspondante est de 0,113848. Puisque cette valeur p n’est pas inférieure à α = 0,05, nous ne disposons pas de preuves suffisantes pour rejeter l’hypothèse nulle.

Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer que la différence moyenne entre les groupes que nous comparons est significativement différente.

Cela nous indique que la variance résiduelle du modèle ANOVA est élevée par rapport à la variation que le modèle peut réellement expliquer.

Variance résiduelle dans les modèles de régression

Dans un modèle de régression, la variance résiduelle est définie comme la somme des carrés des différences entre les points de données prédits et les points de données observés.

Il est calculé comme suit :

Σ(ŷ _je – y _je ) ²

où:

• Σ : un symbole grec qui signifie « somme »
• ŷ _i : Les points de données prédits
• y _i : Les points de données observés

Lorsque nous ajustons un modèle de régression, nous obtenons généralement un résultat qui ressemble à ce qui suit :

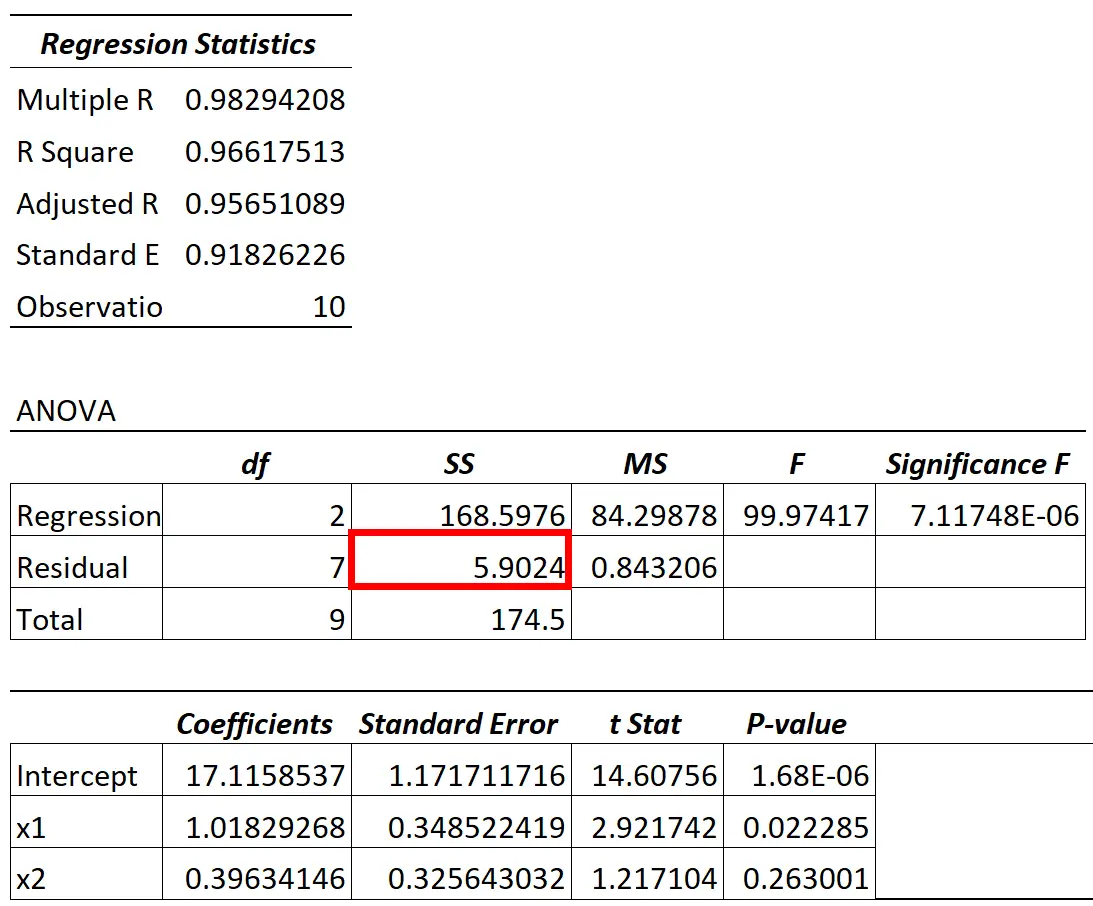
La valeur de la variance résiduelle du modèle ANOVA se trouve dans la colonne SS (« somme des carrés ») pour la variation résiduelle.

Le rapport de la variation résiduelle par rapport à la variation totale dans le modèle nous indique le pourcentage de variation de la variable de réponse qui ne peut pas être expliqué par les variables prédictives du modèle.

Par exemple, dans le tableau ci-dessus, nous calculerions ce pourcentage comme suit :

• Variation inexpliquée = SS Résiduel / SS Total
• Variation inexpliquée = 5,9024 / 174,5
• Variation inexpliquée = 0,0338

On peut également calculer cette valeur à l’aide de la formule suivante :

• Variation inexpliquée = 1 – R ²
• Variation inexpliquée = 1 – 0,96617
• Variation inexpliquée = 0,0338

La valeur R au carré du modèle nous indique le pourcentage de variation de la variable de réponse qui peut être expliqué par la variable prédictive.

Ainsi, plus la variation inexpliquée est faible, plus un modèle est capable d’utiliser les variables prédictives pour expliquer la variation de la variable de réponse.

Ressources additionnelles

Qu’est-ce qu’une bonne valeur R au carré ?
Comment calculer R-carré dans Excel
Comment calculer R-carré dans R