Différence la moins significative de Fisher : définition + exemple

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Les hypothèses utilisées dans une ANOVA sont les suivantes :

H ₀ : Les moyennes sont égales pour chaque groupe.

H _A : Au moins un des moyens est différent des autres.

Si la valeur p de l’ANOVA est inférieure à un certain niveau de signification (comme α = 0,05), nous pouvons rejeter l’hypothèse nulle et conclure qu’au moins une des moyennes du groupe est différente des autres.

Mais pour savoir exactement quels groupes sont différents les uns des autres, nous devons procéder à un test post-hoc.

Un test post-hoc couramment utilisé est le test de différence la moins significative de Fisher .

Pour effectuer ce test, nous calculons d’abord la statistique de test suivante :

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

où:

• t _.025 , _DFw : La valeur t-critique de la table de distribution t avec α = .025 et DF _w correspond aux degrés de liberté au sein des groupes de la table ANOVA.
• MS _W : Les carrés moyens au sein des groupes du tableau ANOVA.
• n ₁ , n ₂ : Les tailles d’échantillon de chaque groupe

Nous pouvons ensuite comparer la différence moyenne entre chaque groupe à cette statistique de test. Si la valeur absolue de la différence moyenne entre deux groupes est supérieure à la statistique du test, nous pouvons déclarer qu’il existe une différence statistiquement significative entre les moyennes des groupes.

L’exemple suivant montre comment effectuer le test de différence la moins significative de Fisher dans la pratique.

Exemple : test de différence de moindre signification de Fisher

Supposons qu’un professeur veuille savoir si trois techniques d’étude différentes conduisent ou non à des résultats d’examen différents parmi les étudiants. Pour tester cela, elle assigne au hasard 10 étudiants à utiliser chaque technique d’étude et enregistre leurs résultats aux examens.

Le tableau suivant montre les résultats aux examens de chaque élève en fonction de la technique d’étude utilisée :

Le professeur effectue une ANOVA unidirectionnelle et obtient les résultats suivants :

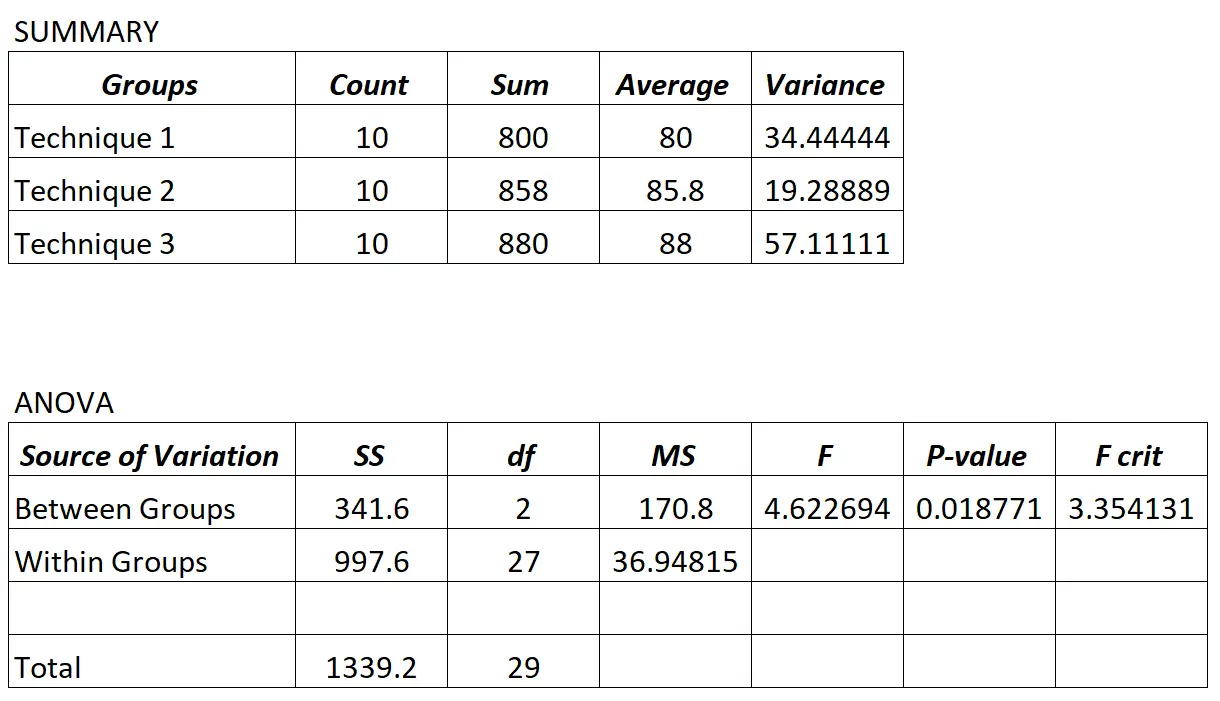
Étant donné que la valeur p dans le tableau ANOVA (0,018771) est inférieure à 0,05, nous pouvons conclure que tous les résultats moyens aux examens entre les trois groupes ne sont pas égaux.

Ainsi, nous pouvons procéder au test de différence la moins significative de Fisher pour déterminer quelles moyennes de groupe sont différentes.

En utilisant les valeurs du résultat de l’ANOVA, nous pouvons calculer la statistique du test de Fisher comme suit :

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948*(1/10 + 1/10)
• LSD = 2,052 * √ 7,3896
• LSD = 5,578

On peut alors calculer la différence moyenne absolue entre chaque groupe :

• Technique 1 contre Technique 2 : |80 – 85,8| = 5,8
• Technique 1 contre Technique 3 : |80 – 88| = 8
• Technique 2 contre Technique 3 : |85,8 – 88| = 2,2

Les différences moyennes absolues entre la technique 1 et la technique 2 et entre la technique 1 et la technique 3 sont supérieures aux statistiques du test de Fisher. Nous pouvons donc conclure que ces techniques conduisent à des scores moyens aux examens statistiquement significativement différents.

Nous pouvons également conclure qu’il n’y a pas de différence significative dans les résultats moyens aux examens entre la technique 2 et la technique 3.