Qu’est-ce qu’un score Z modifié ? (Définition & #038; Exemple)

En statistiques, un score z nous indique à combien d’écarts types une valeur se trouve par rapport à la moyenne . Nous utilisons la formule suivante pour calculer un z-score :

Score Z = (x _i – μ) / σ

où:

• x _i : une seule valeur de données
• μ : la moyenne de l’ensemble de données
• σ : l’écart type de l’ensemble de données

Les scores Z sont souvent utilisés pour détecter les valeurs aberrantes dans un ensemble de données. Par exemple, les observations avec un score z inférieur à -3 ou supérieur à 3 sont souvent considérées comme des valeurs aberrantes.

Cependant, les scores z peuvent être affectés par des valeurs de données inhabituellement grandes ou petites. C’est pourquoi un moyen plus robuste de détecter les valeurs aberrantes consiste à utiliser un score z modifié , calculé comme suit :

Score z modifié = 0,6745 (x _i – x̃) / MAD

où:

• x _i : une seule valeur de données
• x̃ : La médiane de l’ensemble de données
• MAD : l’écart absolu médian de l’ensemble de données

Un score z modifié est plus robuste car il utilise la médiane pour calculer les scores z, par opposition à la moyenne, qui est connue pour être influencée par les valeurs aberrantes .

Iglewicz et Hoaglin recommandent que les valeurs dont les scores z modifiés sont inférieurs à -3,5 ou supérieurs à 3,5 soient étiquetées comme valeurs aberrantes potentielles.

L’exemple étape par étape suivant montre comment calculer les scores z modifiés pour un ensemble de données donné.

Étape 1 : Créer les données

Supposons que nous ayons l’ensemble de données suivant avec 16 valeurs :

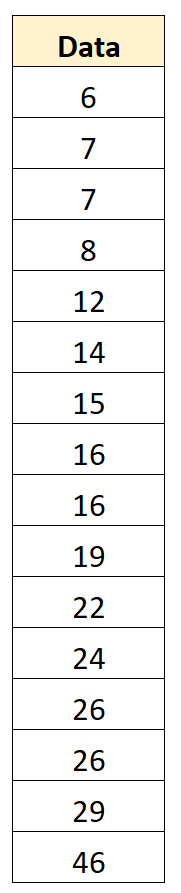
Étape 2 : Trouver la médiane

Ensuite, nous trouverons la médiane. Cela représente le point médian de l’ensemble de données, qui s’avère être 16 .

Étape 3 : Trouver la différence absolue entre chaque valeur et la médiane

Ensuite, nous trouverons la différence absolue entre chaque valeur de données individuelle et la médiane. Par exemple, la différence absolue entre la première valeur de données et la médiane est calculée comme suit :

Différence absolue = |6 – 16| = 10

Nous pouvons utiliser la même formule pour calculer la différence absolue entre chaque valeur de donnée individuelle et la médiane :

Étape 4 : Trouver l’écart médian absolu

Ensuite, nous trouverons l’écart médian absolu. Il s’agit de la médiane de la deuxième colonne, qui s’avère être 8 .

Étape 5 : Trouvez le score Z modifié pour chaque valeur de données

Enfin, nous pouvons calculer le z-score modifié pour chaque valeur de données à l’aide de la formule suivante :

Score z modifié = 0,6745 (x _i – x̃) / MAD

Par exemple, le score z modifié pour la première valeur de données est calculé comme suit :

Score z modifié = 0,6745*(6-16) / 8 = -0,843

Nous pouvons répéter cette formule pour chaque valeur de l’ensemble de données :

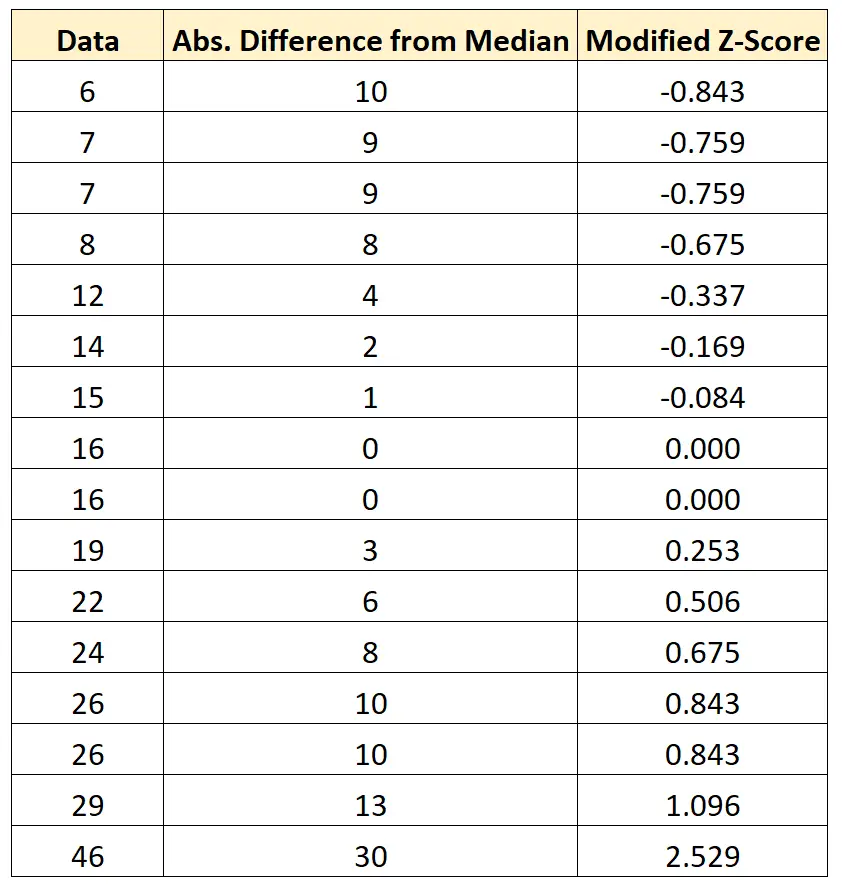
Nous pouvons voir qu’aucune valeur de l’ensemble de données n’a un score z modifié inférieur à -3,5 ou supérieur à 3,5, nous ne qualifions donc aucune valeur de cet ensemble de données de valeur aberrante potentielle.

Comment gérer les valeurs aberrantes

Si une valeur aberrante est présente dans votre ensemble de données, vous disposez de plusieurs options :

• Assurez-vous que la valeur aberrante n’est pas le résultat d’une erreur de saisie de données. Parfois, un individu saisit simplement une mauvaise valeur de données lors de l’enregistrement des données. Si une valeur aberrante est présente, vérifiez d’abord que la valeur a été saisie correctement et qu’il ne s’agissait pas d’une erreur.
• Attribuez une nouvelle valeur à la valeur aberrante . Si la valeur aberrante s’avère être le résultat d’une erreur de saisie de données, vous pouvez décider de lui attribuer une nouvelle valeur telle que la moyenne ou la médiane de l’ensemble de données.
• Supprimez la valeur aberrante. Si la valeur est réellement aberrante, vous pouvez choisir de la supprimer si elle aura un impact significatif sur votre analyse globale. Assurez-vous simplement de mentionner dans votre rapport ou analyse final que vous avez supprimé une valeur aberrante.