Quelle est l’erreur type de l’estimation ? (Définition & #038; Exemple)

L’ erreur type de l’estimation est un moyen de mesurer l’exactitude des prédictions faites par un modèle de régression.

Souvent noté σ _est , il se calcule comme suit :

σ _est = √ Σ(y – ŷ) ² /n

où:

• y : La valeur observée
• ŷ : La valeur prédite
• n : Le nombre total d’observations

L’erreur type de l’estimation nous donne une idée de l’adéquation d’un modèle de régression à un ensemble de données. En particulier:

• Plus la valeur est petite, meilleur est l’ajustement.
• Plus la valeur est grande, plus l’ajustement est mauvais.

Pour un modèle de régression comportant une petite erreur type de l’estimation, les points de données seront étroitement regroupés autour de la droite de régression estimée :

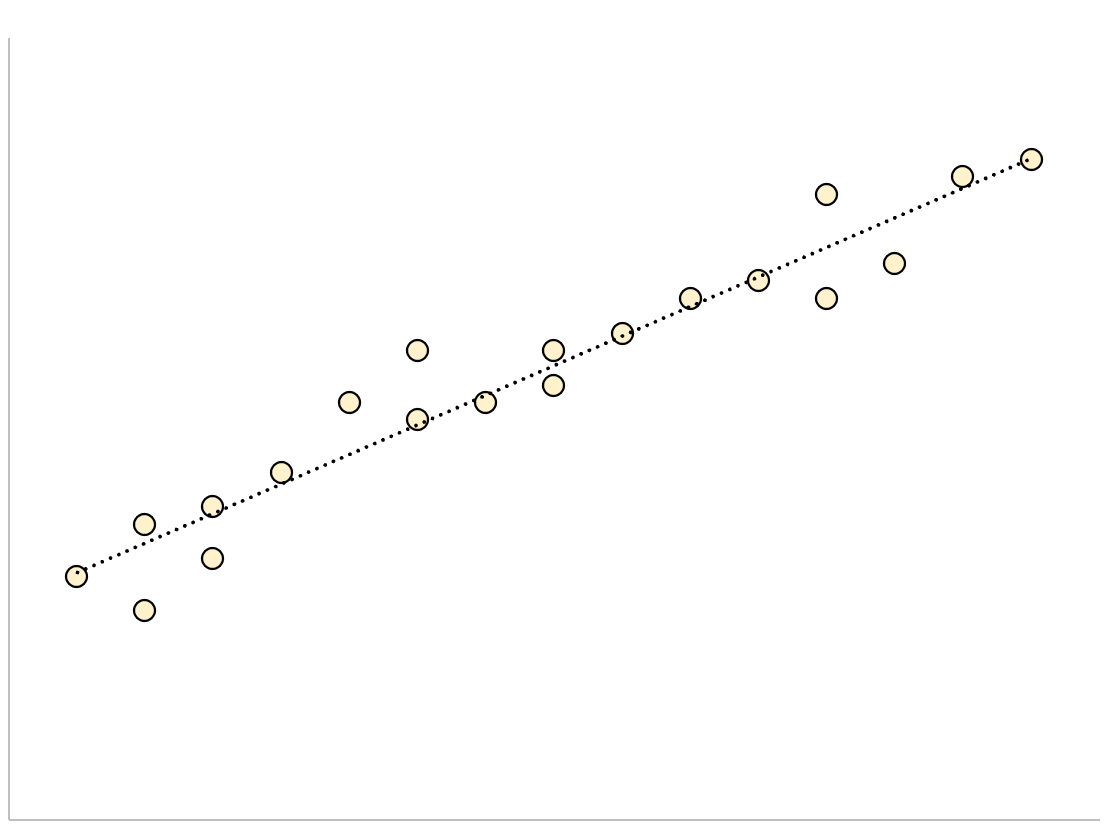
À l’inverse, pour un modèle de régression comportant une erreur type d’estimation importante, les points de données seront plus vaguement dispersés autour de la droite de régression :

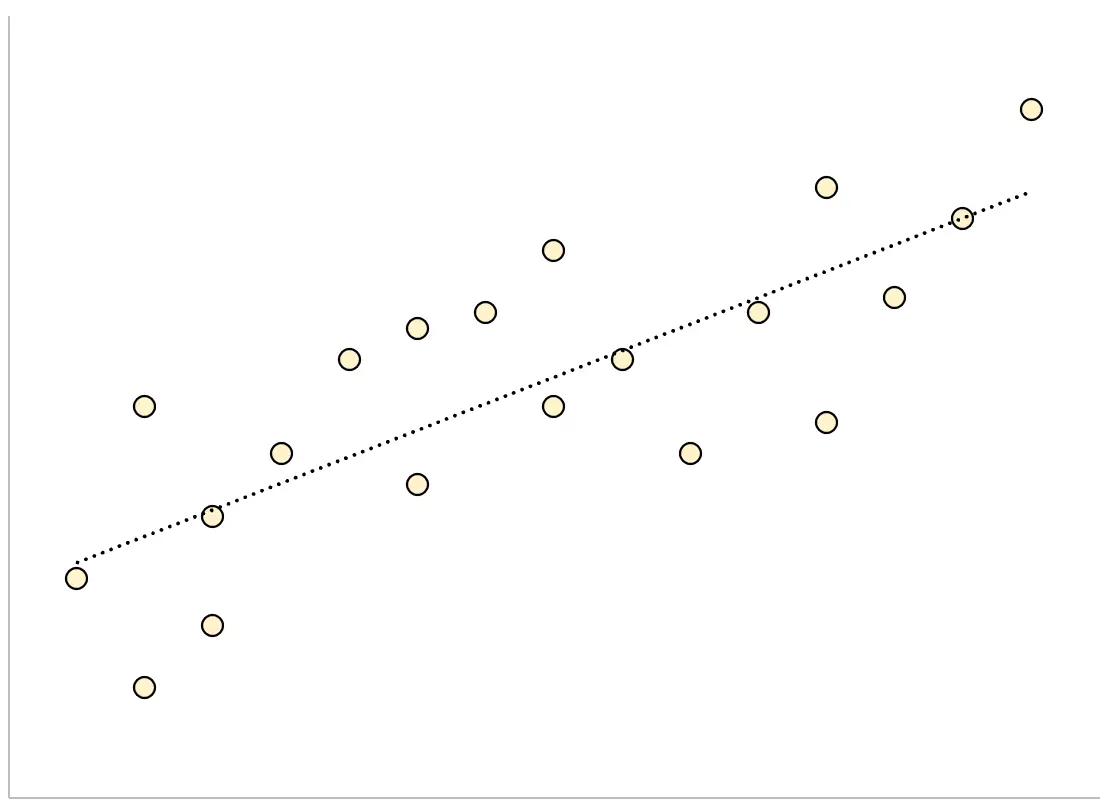
L’exemple suivant montre comment calculer et interpréter l’erreur type de l’estimation pour un modèle de régression dans Excel.

Exemple : erreur type de l’estimation dans Excel

Utilisez les étapes suivantes pour calculer l’erreur type de l’estimation pour un modèle de régression dans Excel.

Étape 1 : Saisissez les données

Tout d’abord, entrez les valeurs de l’ensemble de données :

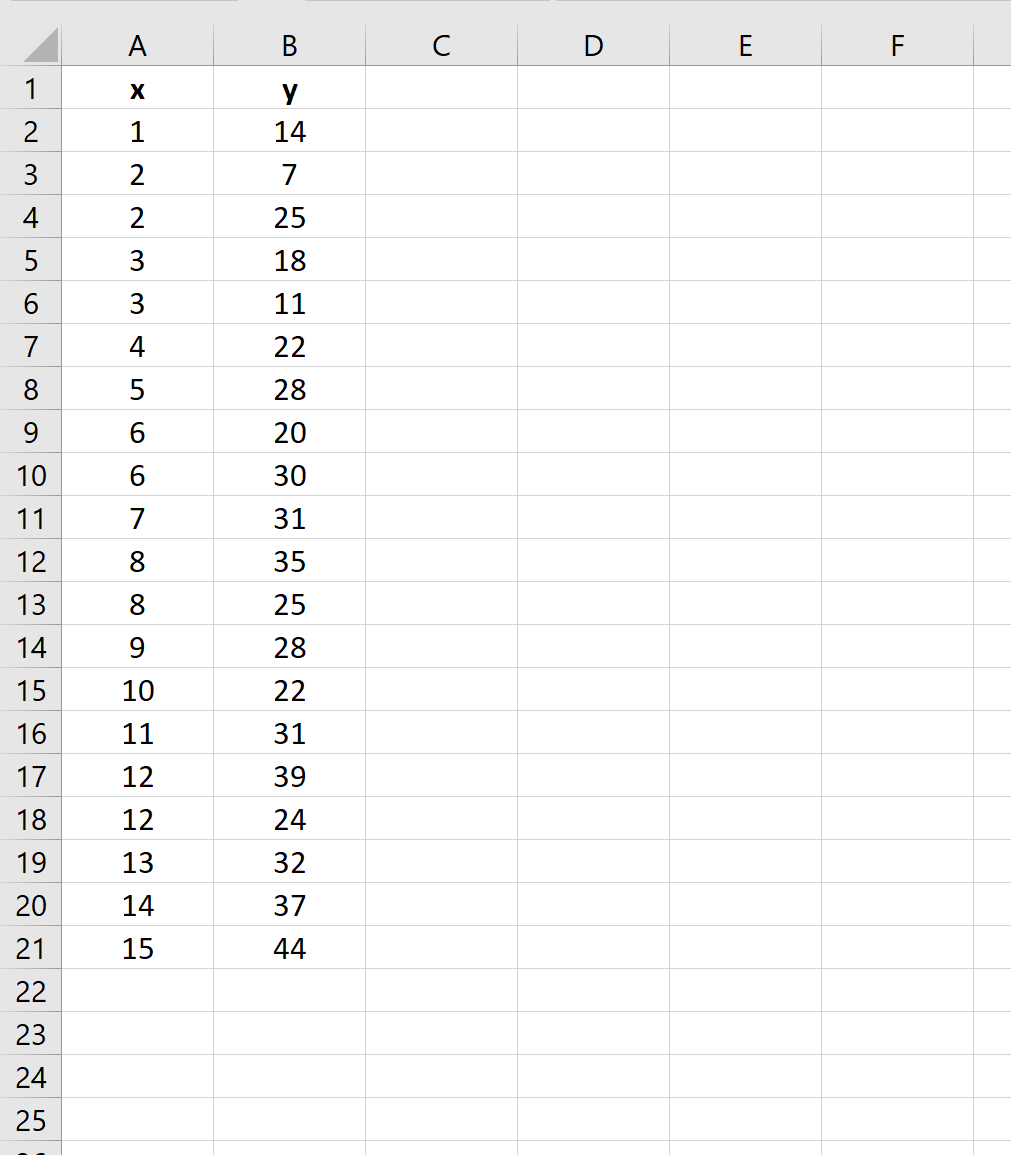
Étape 2 : effectuer une régression linéaire

Ensuite, cliquez sur l’onglet Données le long du ruban supérieur. Cliquez ensuite sur l’option Analyse des données dans le groupe Analyser .

Si vous ne voyez pas cette option, vous devez d’abord charger Analysis ToolPak .

Dans la nouvelle fenêtre qui apparaît, cliquez sur Régression puis cliquez sur OK .

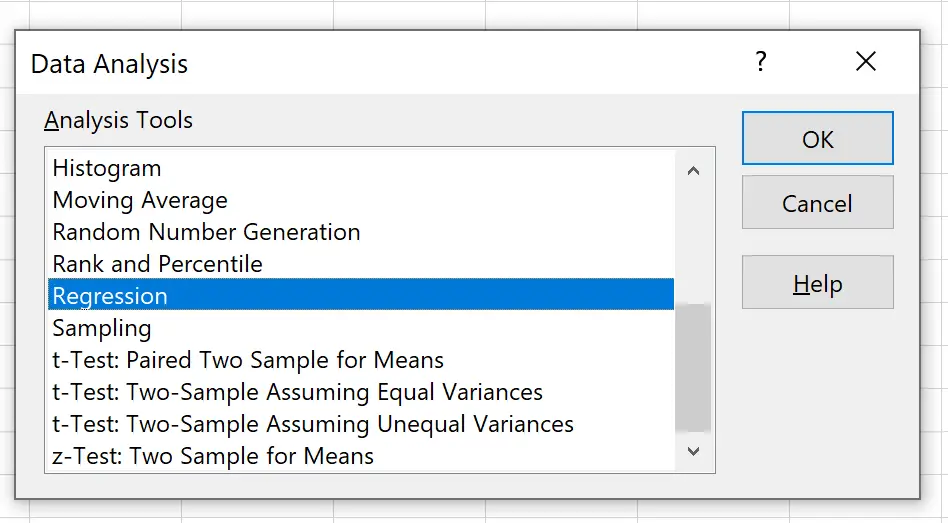
Dans la nouvelle fenêtre qui apparaît, renseignez les informations suivantes :

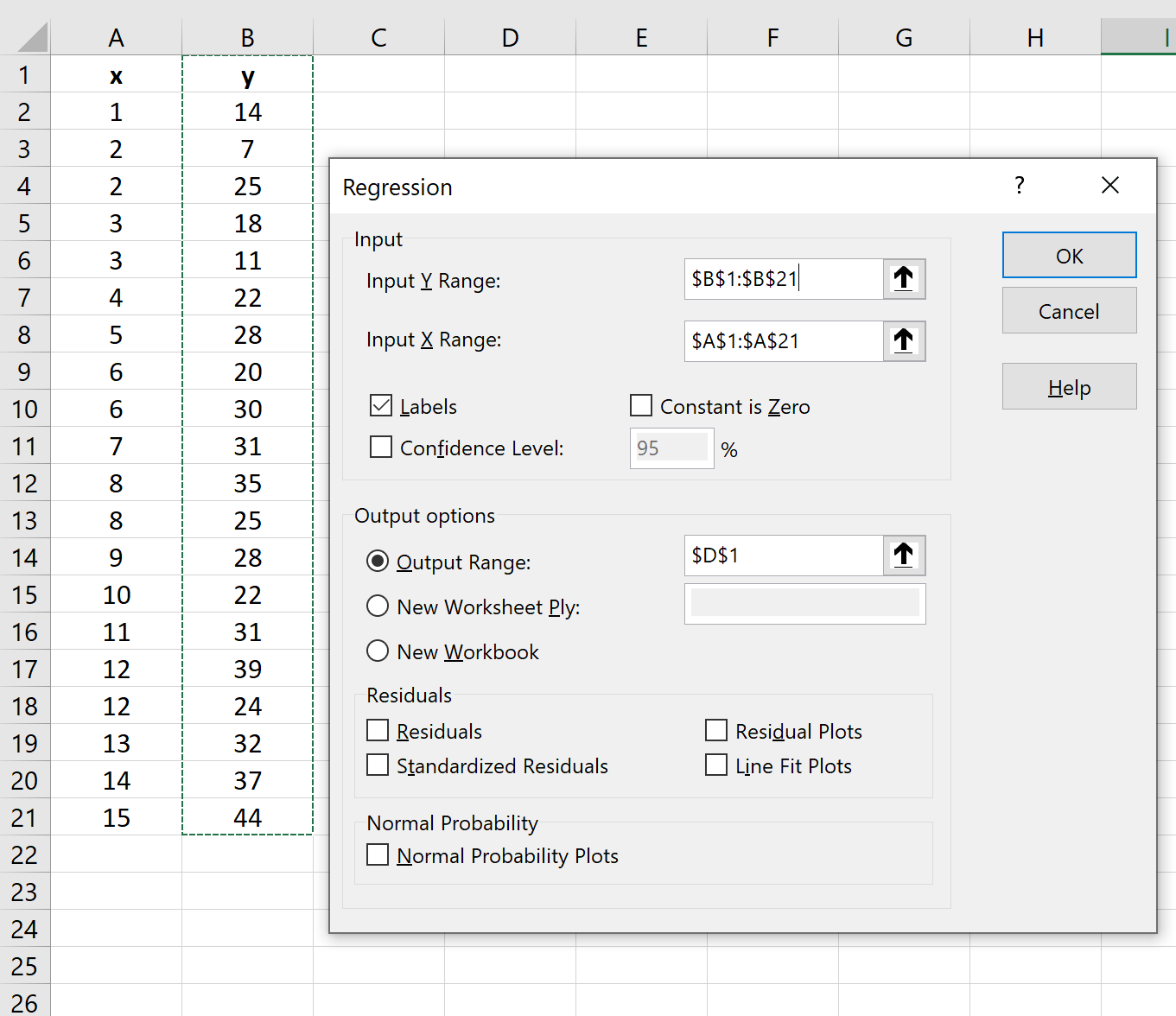
Une fois que vous avez cliqué sur OK , le résultat de la régression apparaîtra :

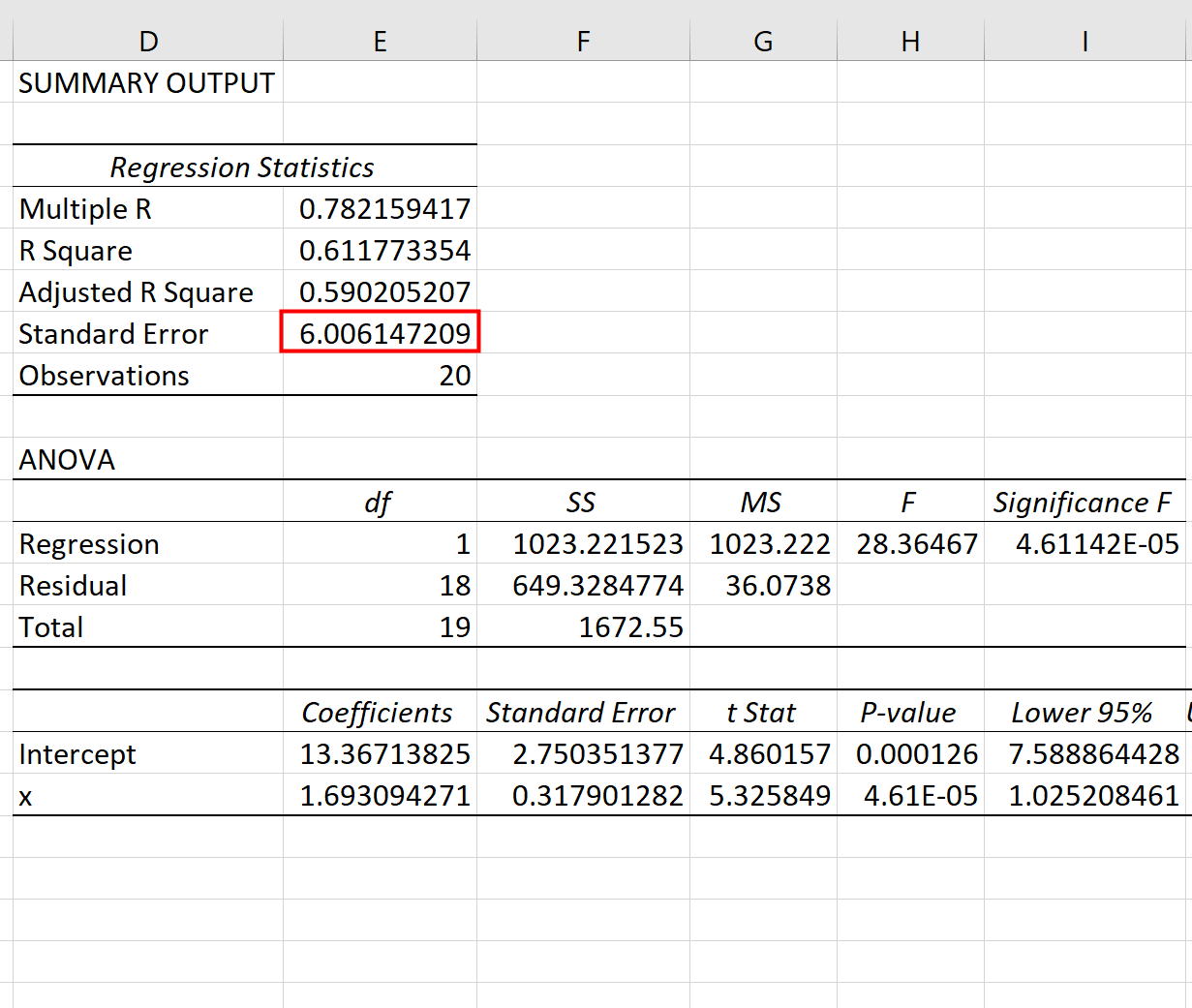
Nous pouvons utiliser les coefficients du tableau de régression pour construire l’équation de régression estimée :

ŷ = 13,367 + 1,693(x)

Et nous pouvons voir que l’erreur type de l’estimation pour ce modèle de régression s’avère être de 6,006 . En termes simples, cela nous indique que le point de données moyen se situe à 6,006 unités de la droite de régression.

Nous pouvons utiliser l’équation de régression estimée et l’erreur type de l’estimation pour construire un intervalle de confiance à 95 % pour la valeur prédite d’un certain point de données.

Par exemple, supposons que x soit égal à 10. En utilisant l’équation de régression estimée, nous prédirions que y serait égal à :

ŷ = 13,367 + 1,693*(10) = 30,297

Et nous pouvons obtenir l’intervalle de confiance à 95 % pour cette estimation en utilisant la formule suivante :

• IC à 95 % = [ŷ – 1,96*σ _est , ŷ + 1,96*σ _est ]

Pour notre exemple, l’intervalle de confiance à 95 % serait calculé comme :

• IC à 95 % = [ŷ – 1,96*σ _est , ŷ + 1,96*σ _est ]
• IC à 95 % = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
• IC à 95 % = [18,525, 42,069]

Ressources additionnelles

Comment effectuer une régression linéaire simple dans Excel
Comment effectuer une régression linéaire multiple dans Excel
Comment créer un tracé résiduel dans Excel