Comment effectuer le test de Scheffe dans Excel

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Si la valeur p globale du tableau ANOVA est inférieure à un certain niveau de signification, alors nous disposons de preuves suffisantes pour affirmer qu’au moins une des moyennes des groupes est différente des autres.

Cependant, cela ne nous dit pas quels groupes sont différents les uns des autres. Cela nous dit simplement que toutes les moyennes du groupe ne sont pas égales.

Afin de savoir exactement quels groupes sont différents les uns des autres, nous devons effectuer un test post-hoc capable de contrôler le taux d’erreur par famille .

L’un des tests post hoc les plus couramment utilisés est le test de Scheffe.

L’exemple étape par étape suivant montre comment effectuer le test de Scheffe dans Excel.

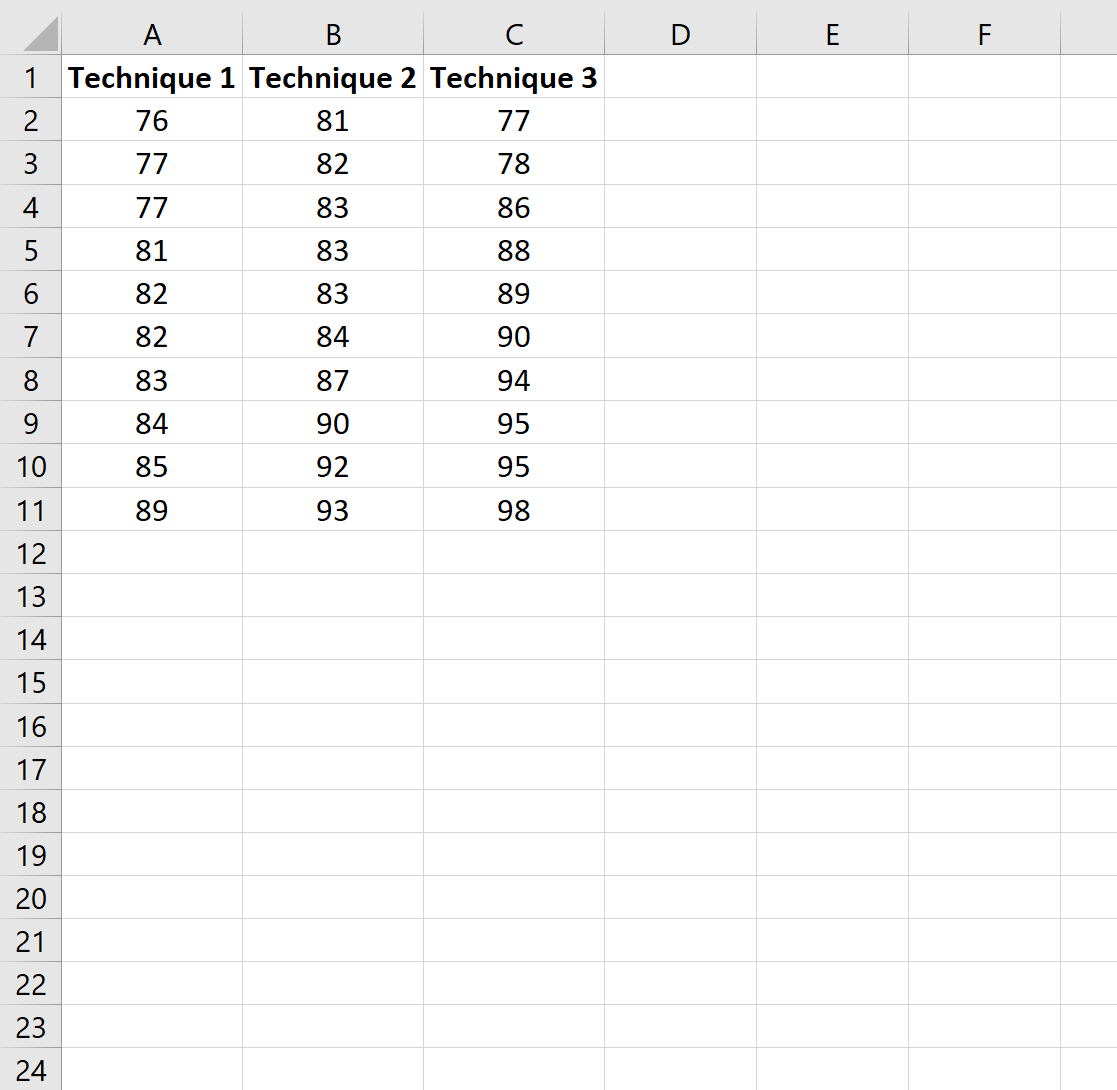
Étape 1 : Saisissez les données

Supposons qu’un enseignant veuille savoir si trois techniques d’étude différentes conduisent ou non à des résultats d’examen différents parmi les élèves. Pour tester cela, elle assigne au hasard 10 étudiants à utiliser chaque technique d’étude et enregistre leurs résultats aux examens.

Tout d’abord, nous saisirons les notes de chaque élève en fonction de la technique d’étude utilisée :

Étape 2 : Effectuer une ANOVA unidirectionnelle

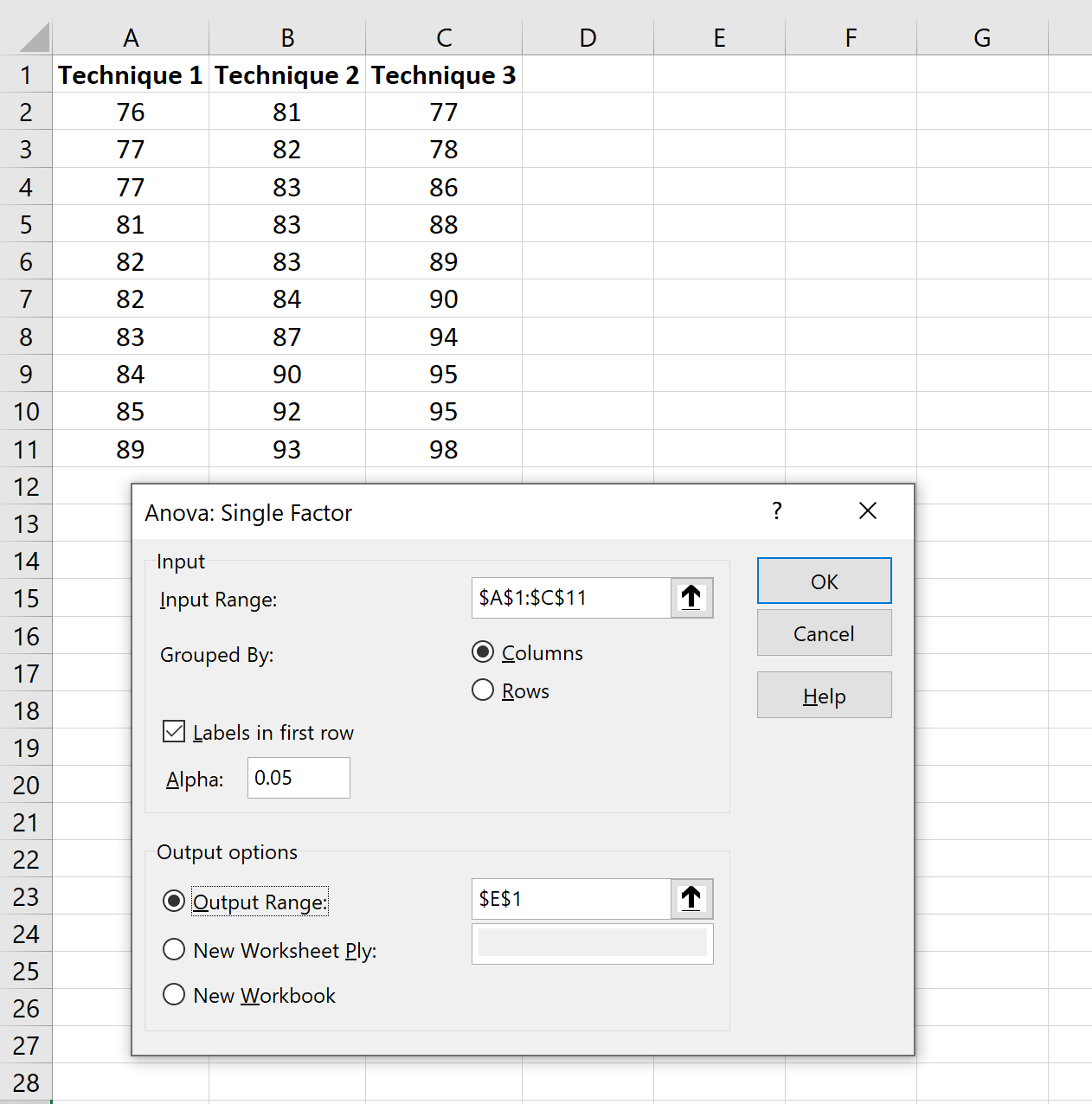
Pour effectuer une ANOVA unidirectionnelle, cliquez sur l’onglet Données le long du ruban supérieur, puis cliquez sur l’option Analyse des données dans le groupe Analyse .

Si vous ne voyez pas cette option, vous devez d’abord charger Analysis ToolPak .

Dans la nouvelle fenêtre qui apparaît, cliquez sur Anova : Single Factor puis cliquez sur OK .

Dans la nouvelle fenêtre qui apparaît, renseignez les informations suivantes :

Une fois que vous avez cliqué sur OK , les résultats de l’ANOVA unidirectionnelle apparaîtront :

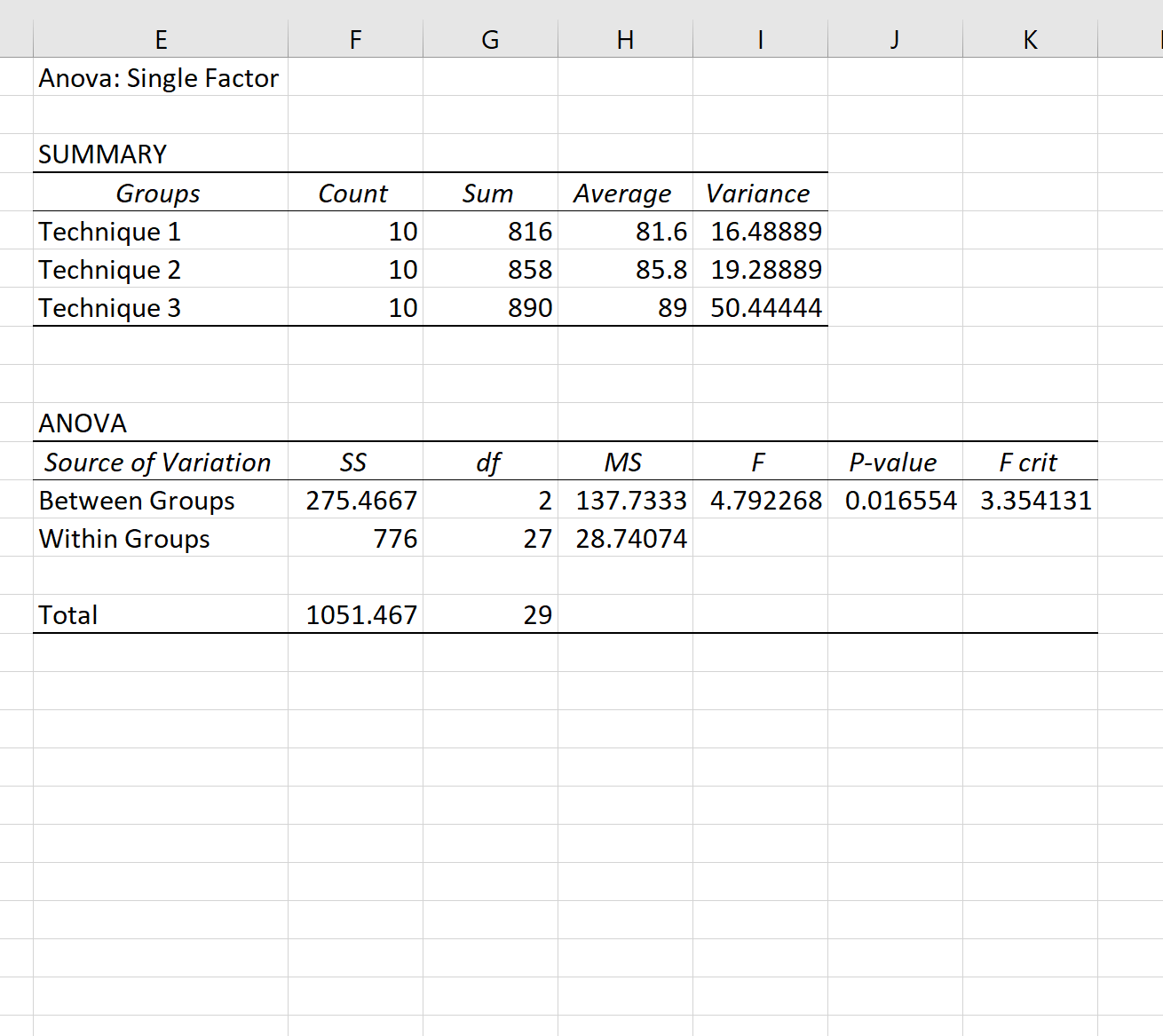
Étant donné que la valeur p globale ( 0,016554 ) dans le tableau ANOVA est inférieure à 0,05, cela signifie que chaque groupe n’a pas la même note moyenne à l’examen.

Ensuite, nous effectuerons le test de Scheffe pour déterminer quels groupes sont différents.

Étape 3 : Effectuer le test de Scheffe

Tout d’abord, nous devons calculer la valeur critique de Scheffe. Ceci est calculé comme suit :

Valeur critique de Scheffe = F Valeur critique * 2

Dans notre exemple, la valeur critique de Scheffe est 3,354131 * 2 = 6,708 .

Ensuite, nous pouvons calculer la statistique F pour chaque comparaison par paire, qui est calculée comme suit :

Statistique F : ( x ₁ – x ₂ ) ² / (MS _dans (1/n ₁ + 1/n ₂ ))

Par exemple, nous pouvons utiliser les formules suivantes pour calculer la statistique F pour la différence par paire entre chaque technique :

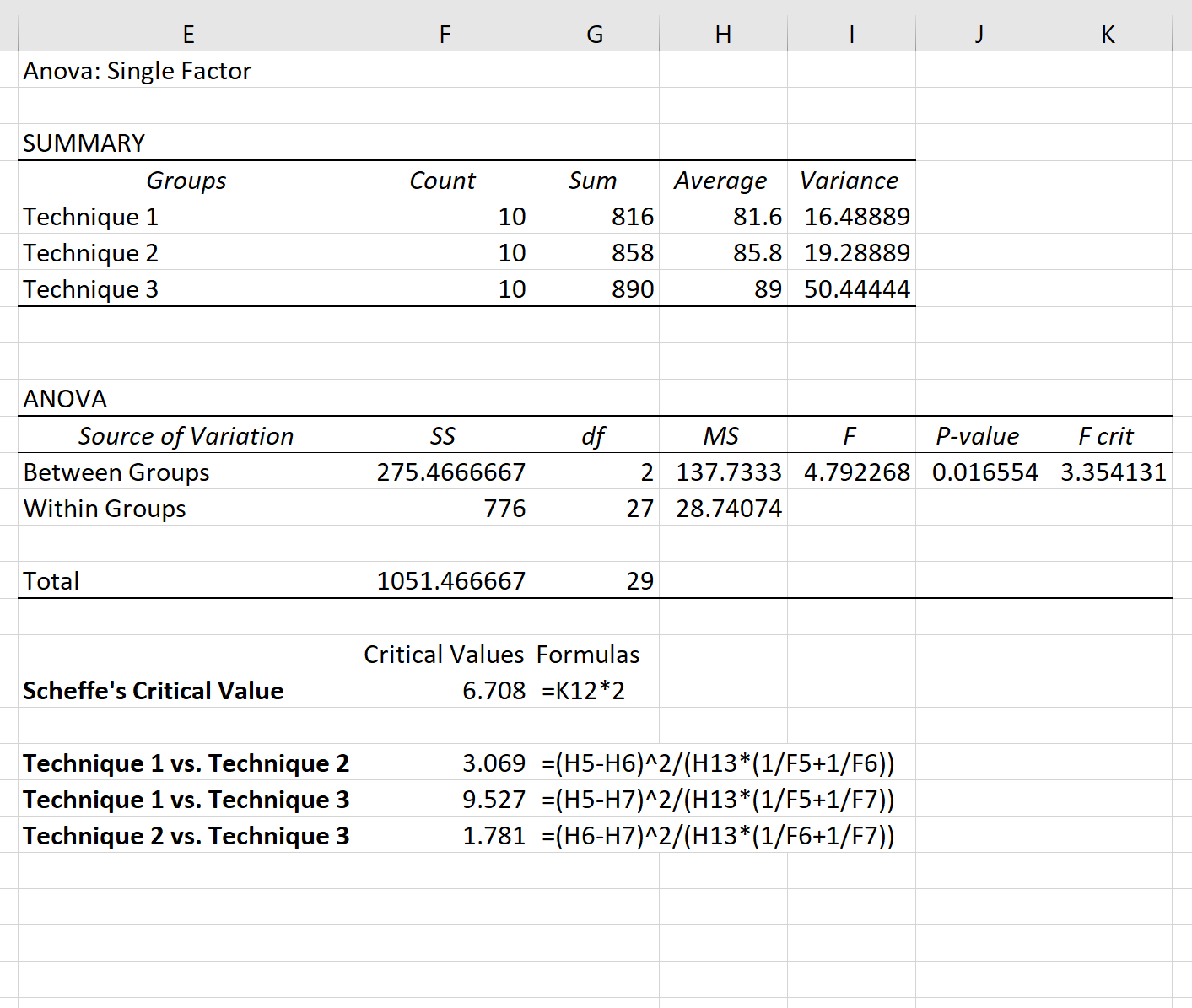
La seule statistique F qui dépasse la valeur critique de Scheffe est celle de la comparaison entre la technique 1 et la technique 3.

Ainsi, les deux seuls groupes statistiquement significativement différents sont la technique 1 et la technique 3.

Ressources additionnelles

Comment effectuer une ANOVA unidirectionnelle dans Excel
Comment effectuer une ANOVA bidirectionnelle dans Excel
Comment effectuer un test post hoc Tukey-Kramer dans Excel