Comment créer une matrice de confusion dans R (étape par étape)

La régression logistique est un type de régression que nous pouvons utiliser lorsque la variable de réponse est binaire.

Une façon courante d’évaluer la qualité d’un modèle de régression logistique consiste à créer une matrice de confusion , qui est un tableau 2 × 2 qui montre les valeurs prédites du modèle par rapport aux valeurs réelles de l’ensemble de données de test.

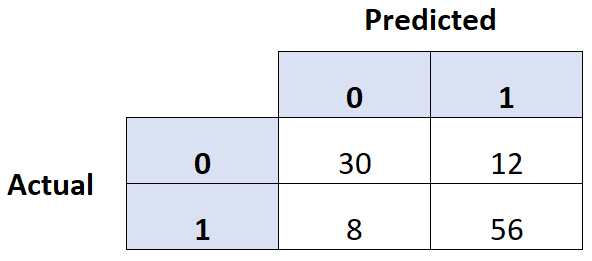
L’exemple suivant, étape par étape, montre comment créer une matrice de confusion dans R.

Étape 1 : Ajuster le modèle de régression logistique

Pour cet exemple, nous utiliserons l’ensemble de données par défaut du package ISLR . Nous utiliserons le statut d’étudiant, le solde bancaire et le revenu annuel pour prédire la probabilité qu’une personne donnée ne rembourse pas son prêt.

Le code suivant montre comment adapter un modèle de régression logistique à cet ensemble de données :

#load necessary packages
library(caret)
library(InformationValue)
library(ISLR)

#load dataset
data <- Default

#split dataset into training and testing set
set.seed(1)
sample <- sample(c(TRUE, FALSE), nrow(data), replace=TRUE, prob=c(0.7,0.3))
train <- data[sample, ]
test <- data[!sample, ]

#fit logistic regression model
model <- glm(default~student+balance+income, family="binomial", data=train)

Étape 2 : Créer la matrice de confusion

Ensuite, nous utiliserons la fonction confusionMatrix() du package caret pour créer une matrice de confusion :

#use model to predict probability of default
predicted <- predict(model, test, type="response")

#convert defaults from "Yes" and "No" to 1's and 0's
test$default <- ifelse(test$default=="Yes", 1, 0)

#find optimal cutoff probability to use to maximize accuracy
optimal <- optimalCutoff(test$default, predicted)[1]

#create confusion matrix
confusionMatrix(test$default, predicted)

     0  1
0 2912 64
1   21 39

Étape 3 : Évaluer la matrice de confusion

Nous pouvons également calculer les métriques suivantes à l’aide de la matrice de confusion :

• Sensibilité : Le « vrai taux de positivité » – le pourcentage d’individus dont le modèle a correctement prédit qu’ils feraient défaut.
• Spécificité : Le « vrai taux négatif » – le pourcentage d’individus que le modèle a correctement prédit ne feraient pas défaut.
• Taux total de classification incorrecte : pourcentage du total de classifications incorrectes effectuées par le modèle.

Le code suivant montre comment calculer ces métriques :

#calculate sensitivity
sensitivity(test$default, predicted)

[1] 0.3786408

#calculate specificity
specificity(test$default, predicted)

[1] 0.9928401

#calculate total misclassification error rate
misClassError(test$default, predicted, threshold=optimal)

[1] 0.027

Le taux d’erreur total de classification est de 2,7 % pour ce modèle.

En général, plus ce taux est faible, plus le modèle est capable de prédire les résultats. Ce modèle particulier s’avère donc très efficace pour prédire si un individu fera défaut ou non.