Test t apparié ou non apparié : quelle est la différence ?

En statistiques, il existe deux types de tests t à deux échantillons :

Test t apparié : utilisé pour comparer les moyennes de deux échantillons lorsque chaque individu d’un échantillon apparaît également dans l’autre échantillon.

Test t non apparié : utilisé pour comparer les moyennes de deux échantillons lorsque chaque individu d’un échantillon est indépendant de chaque individu de l’autre échantillon.

Remarque : Un test t non apparié est plus communément appelé test t pour échantillons indépendants.

Par exemple, supposons qu’un professeur souhaite déterminer si deux techniques d’étude différentes conduisent ou non à des notes moyennes différentes aux examens.

Pour effectuer un test t apparié , il pourrait recruter 10 étudiants et leur faire utiliser une technique d’étude pendant un mois et passer un examen, puis leur faire utiliser la deuxième technique d’étude pendant un mois et passer un autre examen de difficulté égale.

Voici à quoi ressembleraient les données :

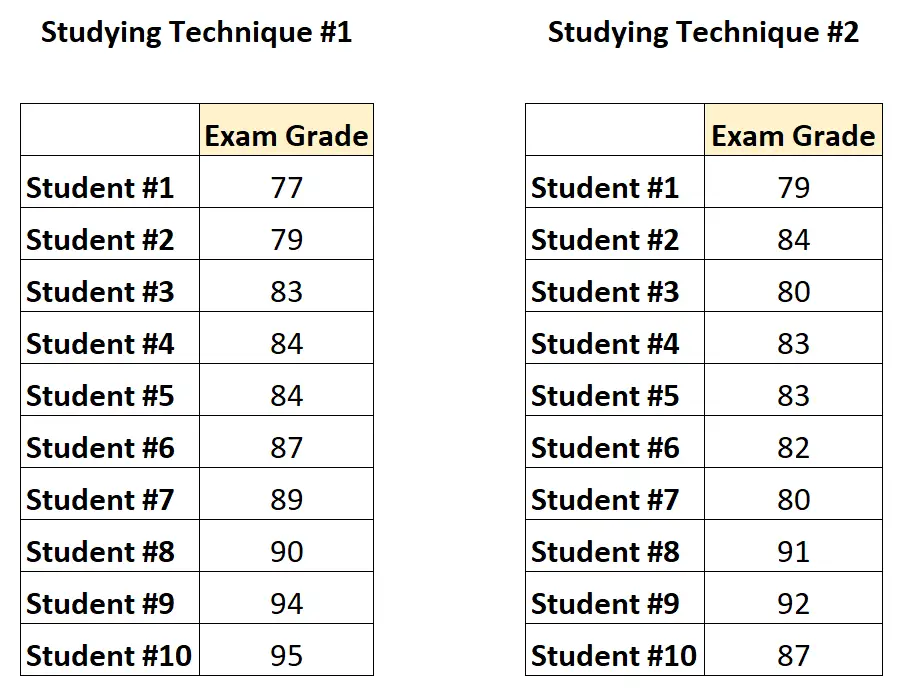
Puisque chaque étudiant apparaît dans chaque groupe, le professeur effectuerait un test t apparié pour déterminer si les scores moyens sont différents entre les deux groupes.

Pour effectuer un test t non apparié , il pourrait recruter 20 étudiants au total et les diviser au hasard en deux groupes de 10. Il pourrait demander à un groupe d’utiliser une technique d’étude pendant un mois et à l’autre groupe d’utiliser la deuxième technique d’étude pendant un mois. mois et demandez à tous les étudiants de passer le même examen.

Voici à quoi ressembleraient les données :

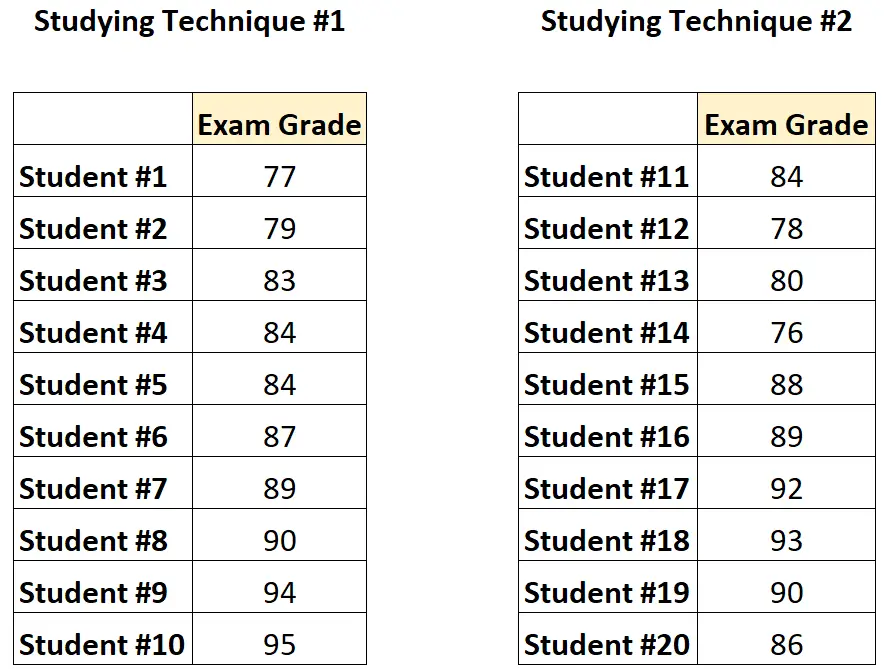
Étant donné que les étudiants d’un groupe sont complètement indépendants des étudiants de l’autre groupe, le professeur effectuerait un test t non apparié pour déterminer si les scores moyens sont différents entre les deux groupes.

Hypothèses

Les tests t appariés et non appariés font tous deux les hypothèses suivantes :

• Les données des deux échantillons ont été obtenues à l’aide d’une méthode d’échantillonnage aléatoire .
• Les données des deux échantillons doivent être distribuées à peu près normalement.
• Il ne devrait y avoir aucune valeur aberrante extrême dans aucun des deux échantillons.

Ces hypothèses doivent être vérifiées avant d’effectuer l’un ou l’autre des tests t pour garantir la fiabilité des résultats du test.

Avantages et inconvénients

Le test t apparié offre les avantages suivants :

• Un échantillon plus petit est requis. Notez que le test t apparié dans l’exemple précédent ne nécessitait que 10 étudiants au total, tandis que le test t non apparié nécessitait 20 étudiants au total.
• Chaque échantillon contient des individus présentant les mêmes caractéristiques. Les deux groupes sont assurés d’avoir des individus ayant des capacités, un intellect, etc. égaux car les mêmes individus apparaissent dans chaque groupe.

Cependant, un test t apparié présente les inconvénients potentiels suivants :

• Le potentiel de réduction de la taille de l’échantillon. Si un individu abandonne l’étude, la taille de l’échantillon de chaque groupe est réduite de un puisque cet individu apparaît dans chaque groupe.
• Le potentiel d’effets d’ordre. Les effets d’ordre font référence aux différences de résultats entre les deux groupes en raison de l’ordre dans lequel les traitements ont été présentés aux individus. Par exemple, un individu peut obtenir de meilleurs résultats au deuxième examen simplement parce qu’il a amélioré ses capacités à passer l’examen plutôt que grâce à sa technique d’étude.

Gardez ces avantages et inconvénients à l’esprit lorsque vous décidez d’utiliser un test t apparié ou non apparié.

Ressources additionnelles

Consultez les didacticiels suivants pour mieux comprendre les tests t appariés :

• Une introduction au test t pour échantillons appariés
• Comment effectuer un test t pour échantillons appariés dans Excel

Et utilisez les didacticiels suivants pour mieux comprendre les tests t non appariés (alias tests t pour échantillons indépendants) :

• Une introduction au test t à deux échantillons
• Comment effectuer un test t à deux échantillons dans Excel