Qu’est-ce qu’un niveau bêta en statistiques ? (Définition & #038; Exemple)

En statistiques, nous utilisons des tests d’hypothèse pour déterminer si une hypothèse concernant un paramètre de population est vraie.

Un test d’hypothèse comporte toujours les deux hypothèses suivantes :

Hypothèse nulle (H ₀ ) : les données de l’échantillon sont cohérentes avec la croyance dominante concernant le paramètre de population.

Hypothèse alternative (H _A ) : les données de l’échantillon suggèrent que l’hypothèse formulée dans l’hypothèse nulle n’est pas vraie. En d’autres termes, une cause non aléatoire influence les données.

Chaque fois que nous effectuons un test d’hypothèse, il y a toujours quatre résultats possibles :

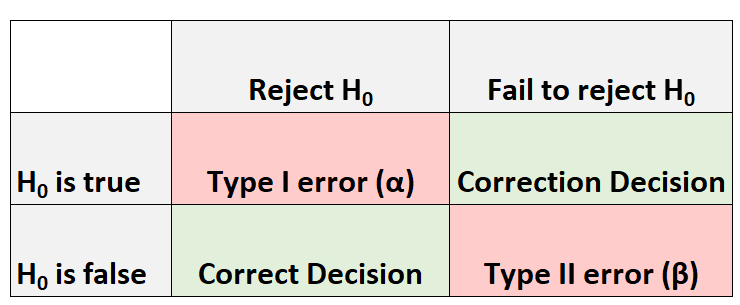
Il existe deux types d’erreurs que nous pouvons commettre :

• Erreur de type I : nous rejetons l’hypothèse nulle alors qu’elle est réellement vraie. La probabilité de commettre ce type d’erreur est notée α .
• Erreur de type II : nous ne parvenons pas à rejeter l’hypothèse nulle alors qu’elle est en réalité fausse. La probabilité de commettre ce type d’erreur est notée β .

La relation entre alpha et bêta

Idéalement, les chercheurs souhaitent que la probabilité de commettre une erreur de type I et la probabilité de commettre une erreur de type II soient faibles.

Il existe cependant un compromis entre ces deux probabilités. Si nous diminuons le niveau alpha, nous pouvons diminuer la probabilité de rejeter une hypothèse nulle alors qu’elle est réellement vraie, mais cela augmente en fait le niveau bêta – la probabilité que nous ne parvenions pas à rejeter l’hypothèse nulle alors qu’elle est fausse.

La relation entre puissance et bêta

La puissance d’un test d’hypothèse fait référence à la probabilité de détecter un effet ou une différence lorsqu’un effet ou une différence est réellement présent. En d’autres termes, c’est la probabilité de rejeter correctement une fausse hypothèse nulle.

Il est calculé comme suit :

Puissance = 1 – β

En général, les chercheurs souhaitent que la puissance d’un test soit élevée afin que, s’il existe un effet ou une différence, le test soit capable de le détecter.

D’après l’équation ci-dessus, nous pouvons voir que la meilleure façon d’augmenter la puissance d’un test est de réduire le niveau bêta. Et la meilleure façon de réduire le niveau bêta est généralement d’augmenter la taille de l’échantillon.

Les exemples suivants montrent comment calculer le niveau bêta d’un test d’hypothèse et démontrent pourquoi l’augmentation de la taille de l’échantillon peut réduire le niveau bêta.

Exemple 1 : calculer le bêta pour un test d’hypothèse

Supposons qu’un chercheur veuille tester si le poids moyen des widgets produits dans une usine est inférieur à 500 onces. On sait que l’écart type des poids est de 24 onces et le chercheur décide de collecter un échantillon aléatoire de 40 widgets.

Il réalisera l’hypothèse suivante à α = 0,05 :

• H ₀ : µ = 500
• H _A : μ < 500

Imaginez maintenant que le poids moyen des widgets produits soit en réalité de 490 onces. En d’autres termes, l’hypothèse nulle doit être rejetée.

Nous pouvons utiliser les étapes suivantes pour calculer le niveau bêta – la probabilité de ne pas rejeter l’hypothèse nulle alors qu’elle devrait en fait être rejetée :

Étape 1 : Trouvez la région de non-rejet.

Selon le calculateur de valeur Z critique , la valeur critique gauche à α = 0,05 est -1,645 .

Étape 2 : Trouvez l’échantillon minimum que nous ne parviendrons pas à rejeter.

La statistique du test est calculée comme z = ( x – μ) / (s/√ n )

Ainsi, nous pouvons résoudre cette équation pour la moyenne de l’échantillon :

• x = µ – z*(s/√ n )
• x = 500 – 1,645*(24/√ 40 )
• x = 493,758

Étape 3 : Déterminez la probabilité que la moyenne minimale de l’échantillon se produise réellement.

Nous pouvons calculer cette probabilité comme suit :

• P(Z ≥ (493,758 – 490) / (24/√ 40 ))
• P(Z ≥ 0,99)

Selon le calculateur CDF normal , la probabilité que Z ≥ 0,99 est de 0,1611 .

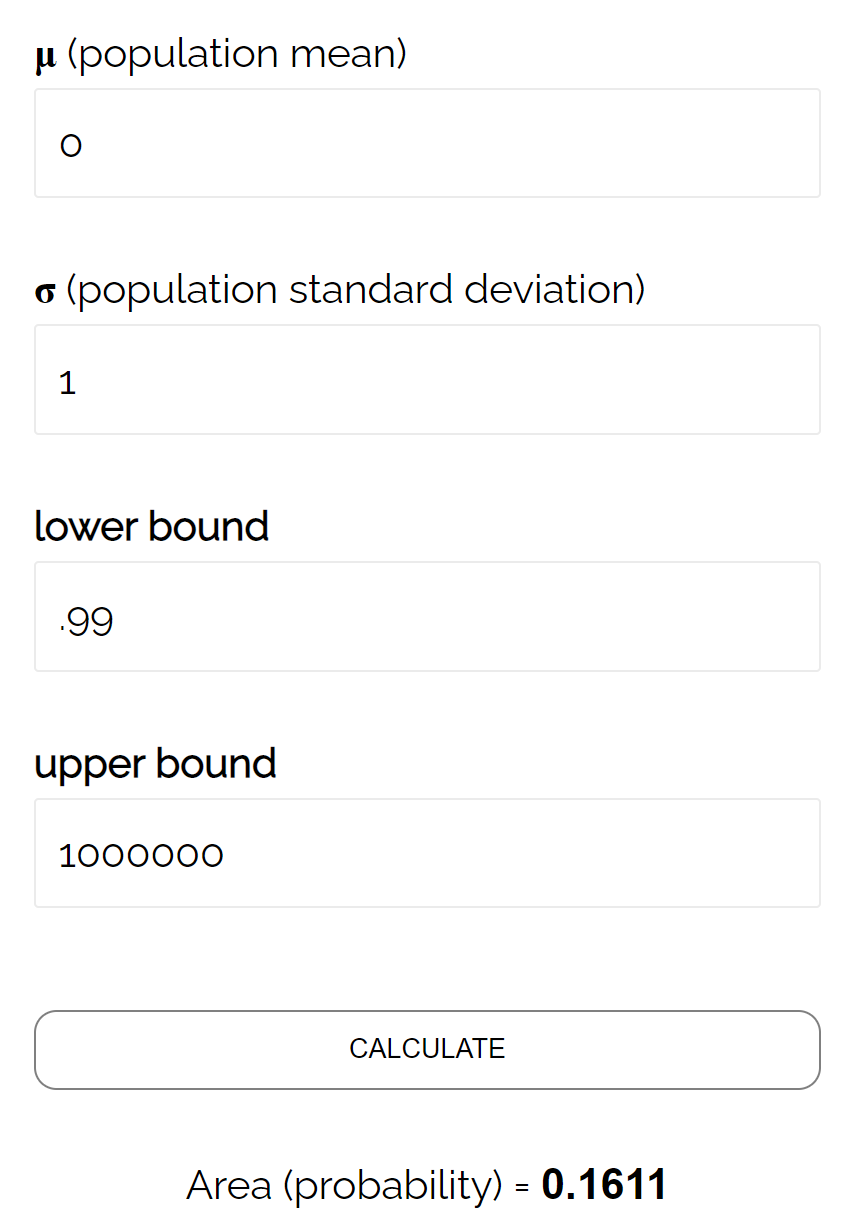
Ainsi, le niveau bêta pour ce test est β = 0,1611. Cela signifie qu’il y a 16,11 % de chances de ne pas détecter la différence si la moyenne réelle est de 490 onces.

Exemple 2 : calculer le bêta pour un test avec une taille d’échantillon plus grande

Supposons maintenant que le chercheur effectue exactement le même test d’hypothèse, mais utilise à la place un échantillon de n = 100 widgets. Nous pouvons répéter les trois mêmes étapes pour calculer le niveau bêta de ce test :

Étape 1 : Trouvez la région de non-rejet.

Selon le calculateur de valeur Z critique , la valeur critique gauche à α = 0,05 est -1,645 .

Étape 2 : Trouvez l’échantillon minimum que nous ne parviendrons pas à rejeter.

La statistique du test est calculée comme z = ( x – μ) / (s/√ n )

Ainsi, nous pouvons résoudre cette équation pour la moyenne de l’échantillon :

• x = µ – z*(s/√ n )
• x = 500 – 1,645*(24/√ 100 )
• x = 496,05

Étape 3 : Déterminez la probabilité que la moyenne minimale de l’échantillon se produise réellement.

Nous pouvons calculer cette probabilité comme suit :

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• P(Z ≥ 2,52)

Selon le calculateur CDF normal , la probabilité que Z ≥ 2,52 est de 0,0059.

Ainsi, le niveau bêta pour ce test est β = 0,0059. Cela signifie qu’il n’y a que 0,59 % de chances de ne pas détecter la différence si la moyenne réelle est de 490 onces.

Notez qu’en augmentant simplement la taille de l’échantillon de 40 à 100, le chercheur a pu réduire le niveau bêta de 0,1611 à 0,0059.

Bonus : utilisez ce calculateur d’erreurs de type II pour calculer automatiquement le niveau bêta d’un test.

Ressources additionnelles

Introduction aux tests d’hypothèses
Comment rédiger une hypothèse nulle (5 exemples)
Une explication des valeurs P et de la signification statistique