Rapport de cotes ajusté : définition + exemples

En statistiques, un rapport de cotes nous indique le rapport entre la probabilité qu’un événement se produise dans un groupe de traitement et la probabilité qu’un événement se produise dans un groupe témoin.

Les rapports de cotes apparaissent le plus souvent dans la régression logistique , qui est une méthode que nous utilisons pour ajuster un modèle de régression comportant une ou plusieurs variables prédictives et une variable de réponse binaire.

Un rapport de cotes ajusté est un rapport de cotes qui a été ajusté pour tenir compte d’autres variables prédictives dans un modèle.

Il est particulièrement utile pour nous aider à comprendre comment une variable prédictive affecte les chances qu’un événement se produise, après ajustement pour l’effet d’autres variables prédictives.

L’exemple suivant illustre la différence entre un rapport de cotes et un rapport de cotes ajusté.

Exemple : Calcul des rapports de cotes ajustés

Supposons que nous souhaitions comprendre si l’âge d’une mère affecte la probabilité d’avoir un bébé avec un faible poids à la naissance.

Pour explorer cela, nous pouvons effectuer une régression logistique en utilisant l’âge comme variable prédictive et le faible poids à la naissance (oui ou non) comme variable de réponse .

Supposons que nous collections des données sur 300 mères et ajustions un modèle de régression logistique. Voici les résultats:

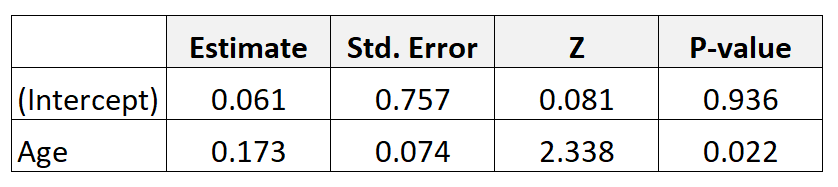
Pour obtenir l’odds ratio pour l’âge, il suffit d’exponentier l’estimation du coefficient à partir du tableau : e ^0,173 = 1,189 .

Cela nous indique qu’une augmentation d’un an en âge est associée à une augmentation de 1,189 des chances qu’un bébé ait un faible poids à la naissance. En d’autres termes, les chances d’avoir un bébé avec un faible poids à la naissance augmentent de 18,9 % pour chaque augmentation annuelle supplémentaire de l’âge.

Ce rapport de cotes est appelé rapport de cotes « brut » ou rapport de cotes « non ajusté » car il n’a pas été ajusté pour tenir compte des autres variables prédictives du modèle puisqu’il s’agit de la seule variable prédictive du modèle.

Mais supposons que nous cherchions à comprendre si l’âge d’une mère et ses habitudes tabagiques affectent la probabilité d’avoir un bébé avec un faible poids à la naissance.

Pour explorer cela, nous pouvons effectuer une régression logistique en utilisant l’âge et le tabagisme (oui ou non) comme variables prédictives et le faible poids à la naissance comme variable de réponse .

Supposons que nous collections des données sur 300 mères et ajustions un modèle de régression logistique. Voici les résultats:

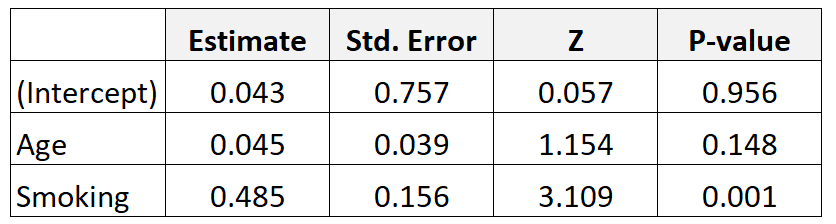
Voici comment interpréter les résultats :

Âge : Le rapport de cotes ajusté pour l’âge est calculé comme suit : e ^0,045 = 1,046 . Cela signifie que les chances d’avoir un bébé avec un faible poids à la naissance augmentent de 4,6 % pour chaque augmentation annuelle supplémentaire de l’âge, en supposant que la variable tabagisme reste constante.

Par exemple, supposons que la mère A et la mère B fument toutes les deux. Si la mère A a un an de plus que la mère B, alors la probabilité que la mère A ait un bébé de faible poids à la naissance est 1,046 fois la probabilité que la mère B ait un bébé de faible poids à la naissance.

Tabagisme : Le rapport de cotes ajusté pour le tabagisme est calculé comme suit : e ^,485 = 1,624 . Cela signifie que les chances d’avoir un bébé avec un faible poids à la naissance augmentent de 62,4 % si la mère fume (par rapport à ne pas fumer), en supposant que l’ âge variable reste constant.

Par exemple, supposons que la mère A et la mère B aient toutes deux 30 ans. Si la mère A fume pendant la grossesse et que la mère B ne fume pas, alors les chances que la mère A ait un bébé de faible poids à la naissance sont 62,4 % plus élevées que les chances que la mère B ait un bébé de faible poids à la naissance.

Notez que le rapport de cotes ajusté pour l’âge est inférieur au rapport de cotes non ajusté de l’exemple précédent. En effet, lorsque d’autres variables prédictives augmentent les chances que la variable de réponse se produise, le rapport de cotes ajusté pour une variable prédictive déjà présente dans le modèle diminuera toujours.

Résumé : rapport de cotes par rapport au rapport de cotes ajusté

Un rapport de cotes (parfois appelé rapport de cotes « brut ») est utile pour nous indiquer comment les changements dans une variable prédictive affectent les chances qu’une variable de réponse se produise.

Un rapport de cotes ajusté est utile pour nous indiquer comment les changements dans une variable prédictive affectent les chances qu’une variable de réponse se produise, après avoir contrôlé les autres variables prédictives dans un modèle.

Ressources additionnelles

Introduction à la régression logistique
Comment effectuer une régression logistique dans R
Comment effectuer une régression logistique en Python