Le biais de Berkson : définition + exemples

Le biais de Berkson est un type de biais qui se produit dans la recherche lorsque deux variables semblent être corrélées négativement dans les données d’un échantillon, mais sont en réalité corrélées positivement dans la population globale.

Par exemple, supposons que Tom souhaite étudier la corrélation entre la qualité des hamburgers et celle des milkshakes dans les restaurants locaux.

Il sort et collecte les données suivantes sur sept restaurants différents :

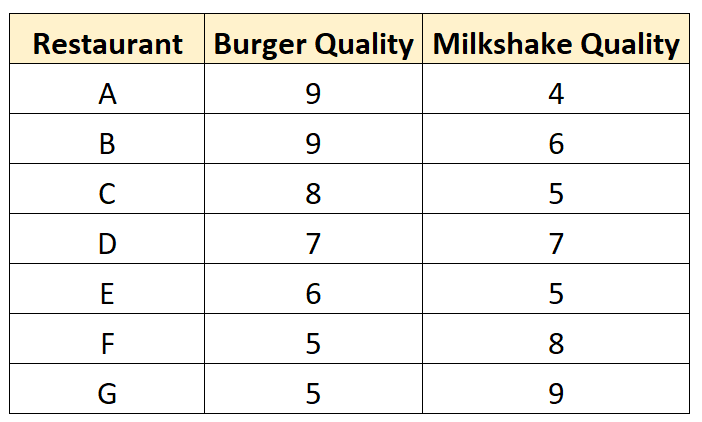
Il crée un nuage de points pour visualiser les données :

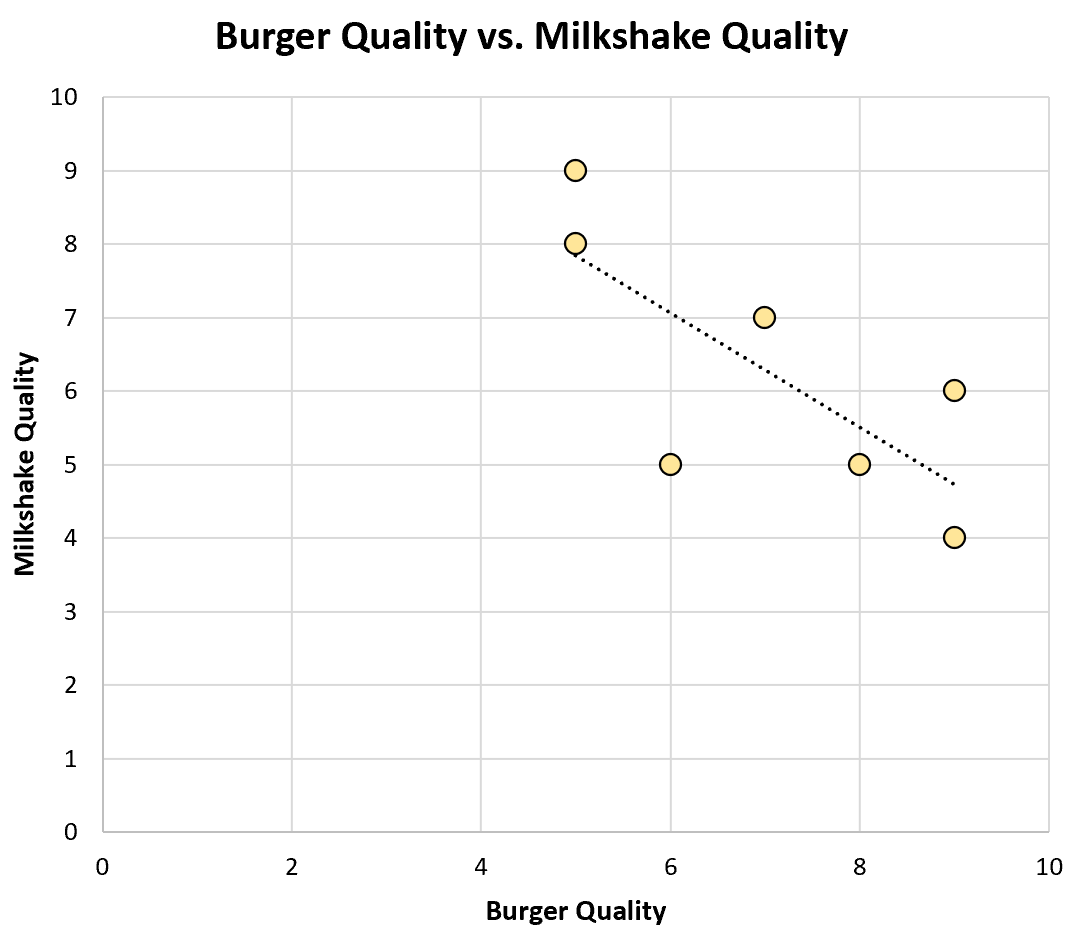
Le coefficient de corrélation de Pearson entre ces deux variables est de -0,75 , ce qui correspond à une forte corrélation négative.

Cette découverte est contre-intuitive pour Tom : il penserait que les restaurants qui font de bons hamburgers font aussi de bons milkshakes.

Cependant, il s’avère que Tom a simplement ignoré tous les restaurants de la ville qui préparent à la fois de mauvais hamburgers et de mauvais milkshakes.

S’il avait visité ces restaurants, il aurait collecté l’ensemble de données suivant :

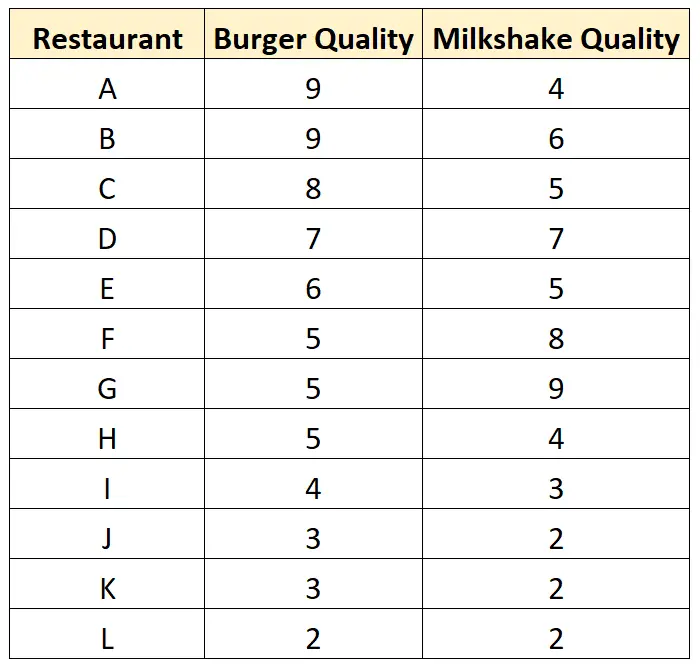
Et voici à quoi ressemble un nuage de points pour cet ensemble de données :

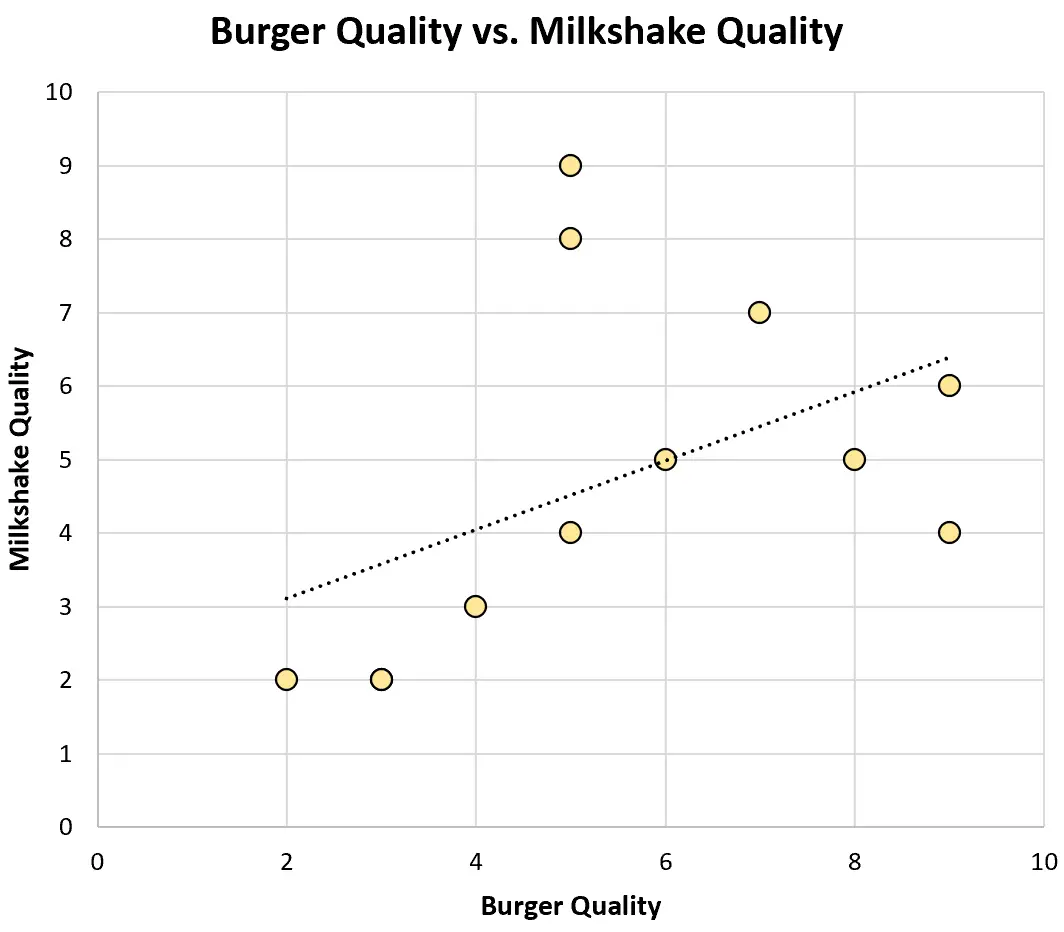
Le coefficient de corrélation de Pearson entre les deux variables s’avère être de 0,46 , ce qui représente une corrélation positive moyennement forte.

En examinant uniquement un sous-ensemble de restaurants de la ville, Tom a conclu à tort qu’il existait une corrélation négative entre la qualité des hamburgers et celle des milkshakes.

En réalité, il s’avère qu’il existe une relation positive (comme on pouvait s’y attendre) entre ces deux variables. Il s’agit là d’un exemple classique du parti pris de Berkson.

Consultez les exemples suivants pour découvrir d’autres scénarios dans lesquels le biais de Berkson se produit dans la pratique.

Exemple 1 : Admissions à l’université

Supposons qu’un collège n’admette que les étudiants qui ont un GPA et un score ACT suffisamment élevés.

Il est bien connu que ces deux variables sont positivement corrélées, mais il s’avère que parmi les étudiants qui décident d’aller dans un collège particulier, il semble y avoir une corrélation négative entre les deux.

Cependant, cette corrélation négative ne se produit que parce que les étudiants qui ont à la fois un score GPA et ACT élevés peuvent fréquenter une université d’élite, tandis que les étudiants qui ont à la fois un score GPA et ACT faibles ne sont pas admis du tout.

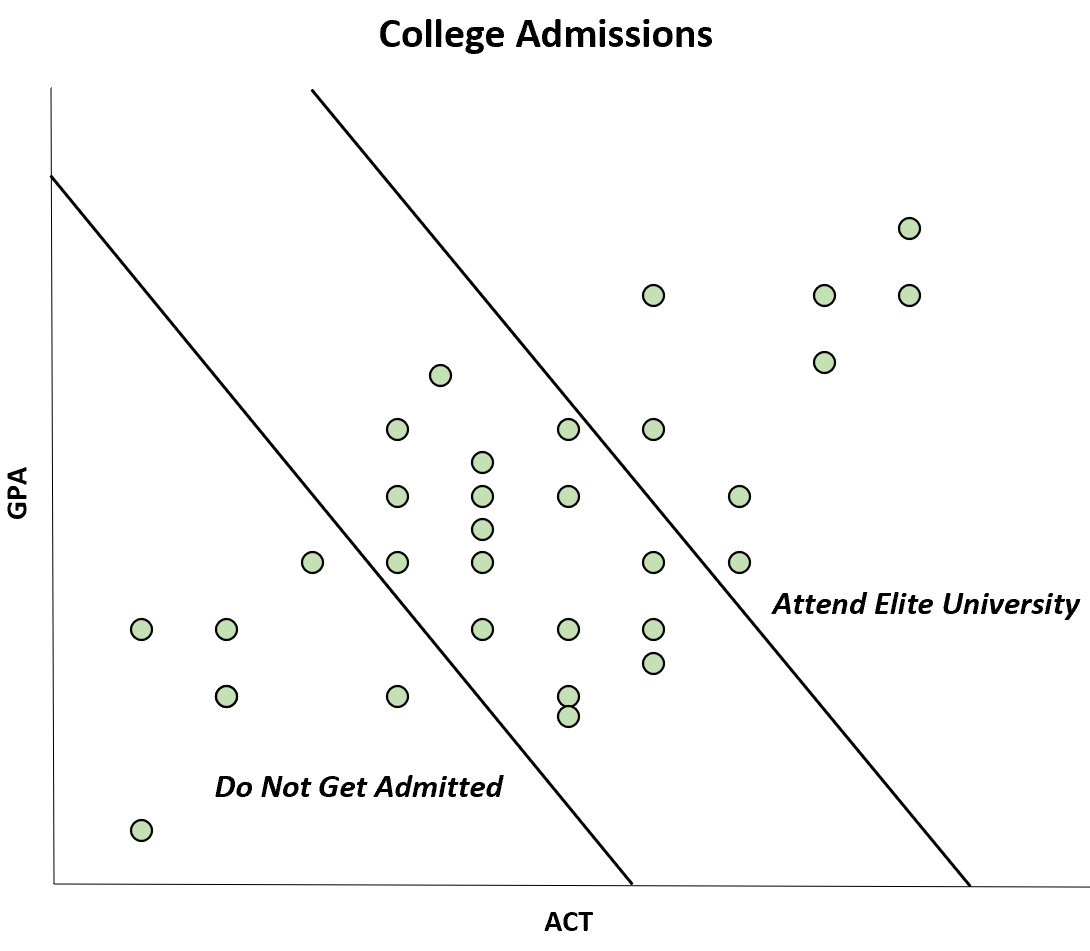
Bien que la corrélation entre ACT et GPA soit positive dans la population, la corrélation semble négative dans l’échantillon. Il s’agit là d’un cas de parti pris de Berkson.

Exemple 2 : Préférences de rencontres

De nombreuses personnes ne sortiront qu’avec des partenaires à la fois attirants et dotés d’une bonne personnalité.

Dans le monde réel, il se peut qu’il n’y ait aucune corrélation entre ces deux variables, mais lors de la réduction du bassin de rencontres, un individu peut complètement ignorer les partenaires potentiels qui sont à la fois peu attrayants et dotés d’une bonne personnalité.

Ainsi, parmi les partenaires potentiels, il peut sembler qu’il existe une corrélation négative entre ces deux variables : les personnes les plus attirantes ont une moins bonne personnalité et les personnes ayant une meilleure personnalité semblent moins attirantes.

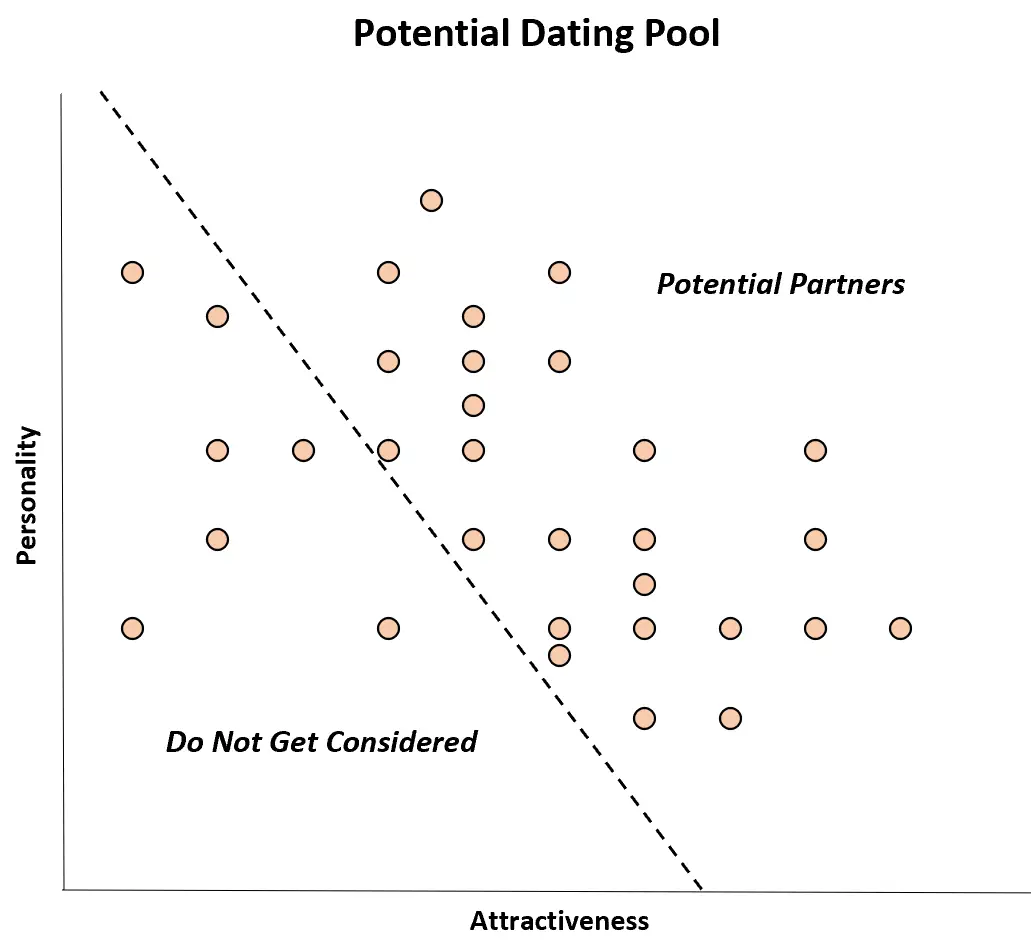
Bien qu’il n’y ait pas de corrélation entre ces deux variables dans la population, il semble y avoir une corrélation négative dans l’échantillon de partenaires potentiels. Il s’agit simplement d’un cas de parti pris de Berkson.

Comment prévenir le biais de Berkson

Le moyen le plus évident d’éviter le biais de Berkson dans les études de recherche est de collecter un échantillon aléatoire simple au sein d’une population. Autrement dit, assurez-vous que chaque membre de la population d’intérêt a une chance égale d’être inclus dans l’échantillon.

Par exemple, si vous étudiez la prévalence des maladies dans un certain pays, vous devez collecter un échantillon d’individus dans tout le pays, et pas seulement ceux qu’il est facile d’atteindre dans les hôpitaux.

En utilisant un échantillon aléatoire simple, les chercheurs peuvent maximiser les chances que leur échantillon soit représentatif de la population, ce qui signifie qu’ils peuvent généraliser en toute confiance leurs conclusions à partir de l’échantillon à la population globale.