Comment effectuer une correction Bonferroni dans Excel
Une correction de Bonferroni fait référence au processus d’ajustement du niveau alpha (α) pour une famille de tests statistiques afin de contrôler la probabilité de commettre une erreur de type I.
La formule d’une correction Bonferroni est la suivante :
α nouveau = α original / n
où:
- α original : Le niveau α d’origine
- n : Le nombre total de comparaisons ou de tests effectués
Par exemple, si nous effectuons trois tests statistiques à la fois et souhaitons utiliser α = 0,05 pour chaque test, la correction de Bonferroni nous indique que nous devons utiliser α new = 0,01667 .
α nouveau = α original / n = 0,05 / 3 = 0,01667
Ainsi, nous ne devrions rejeter l’hypothèse nulle de chaque test individuel que si la valeur p du test est inférieure à 0,01667.
Ce type de correction est souvent effectué dans les tests post-hoc suite à une ANOVA lorsque l’on souhaite comparer plusieurs moyennes de groupes à la fois.
L’exemple étape par étape suivant montre comment effectuer une correction de Bonferroni après une ANOVA unidirectionnelle dans Excel.
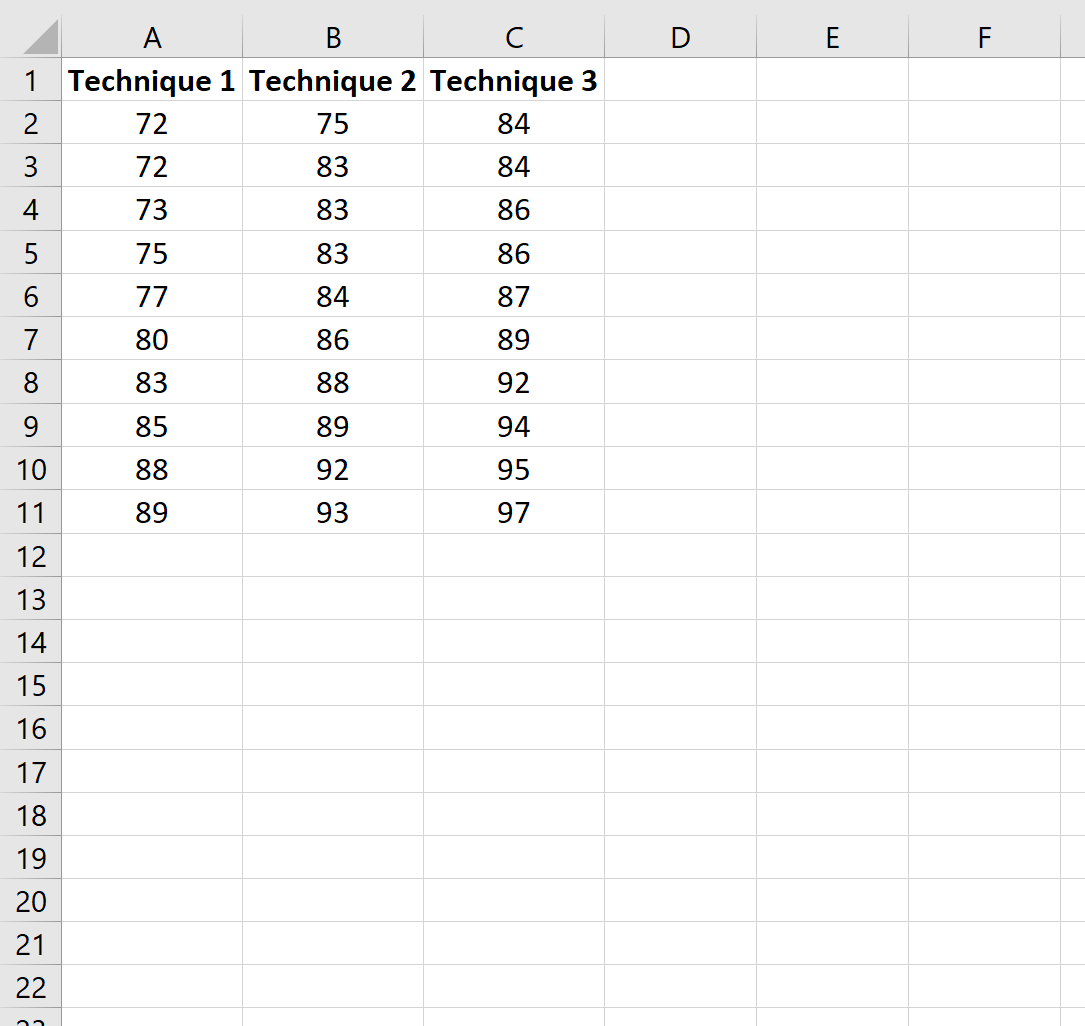
Étape 1 : Créer les données
Tout d’abord, créons un faux ensemble de données qui montre les résultats des étudiants qui ont utilisé l’une des trois techniques d’étude différentes pour se préparer à l’examen :
Étape 2 : Effectuer l’ANOVA unidirectionnelle
Effectuons ensuite une ANOVA unidirectionnelle pour déterminer si les résultats moyens aux examens sont égaux dans les trois groupes.
Tout d’abord, mettez en surbrillance toutes les données, y compris les en-têtes de colonnes :
Ensuite, cliquez sur l’onglet Données le long du ruban supérieur, puis cliquez sur Analyse des données :

Si cette option n’est pas disponible, vous devez d’abord charger Analysis ToolPak .
Dans la fenêtre qui apparaît, cliquez sur Anova : Single Factor puis cliquez sur OK .
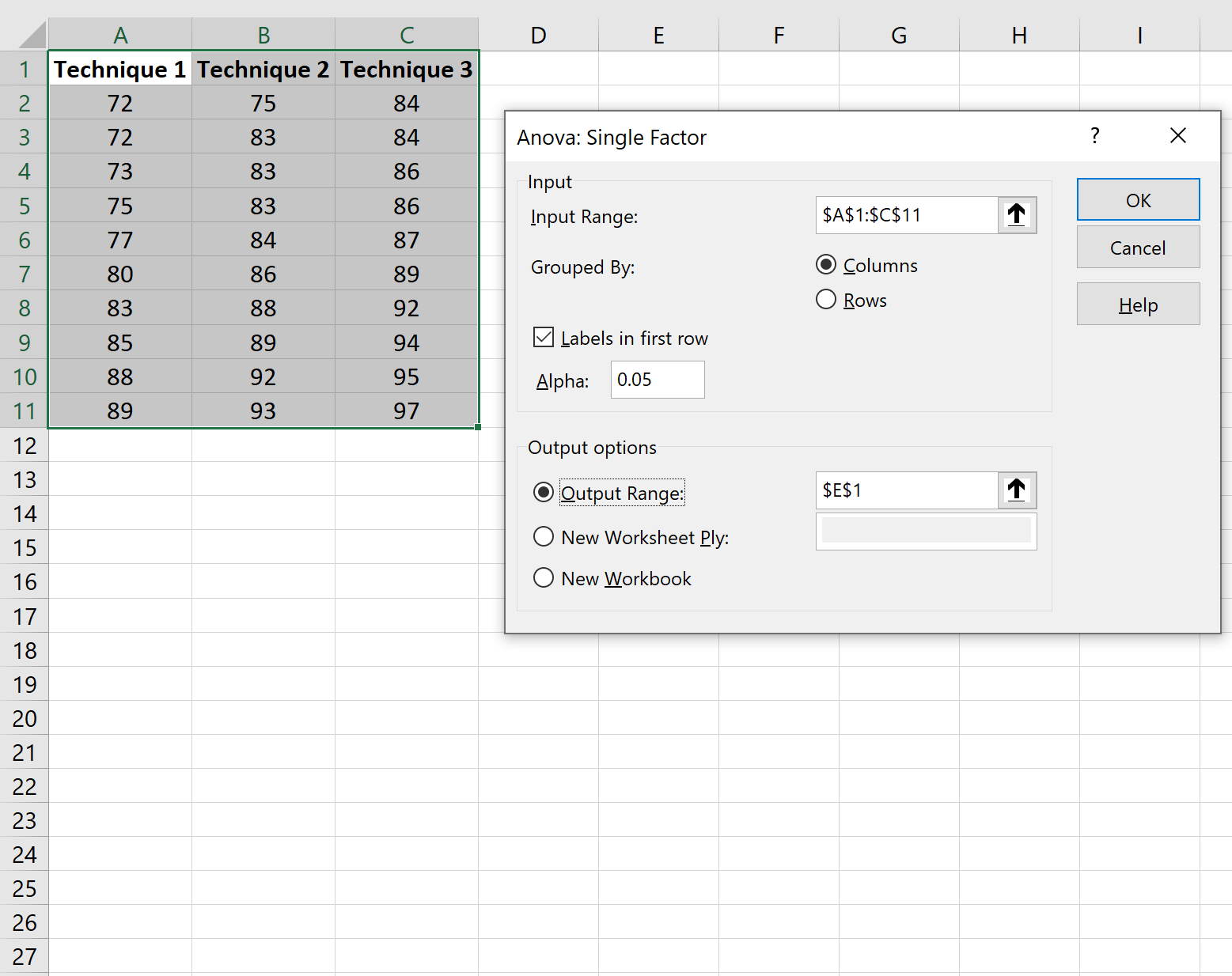
Remplissez les informations suivantes, puis cliquez sur OK :
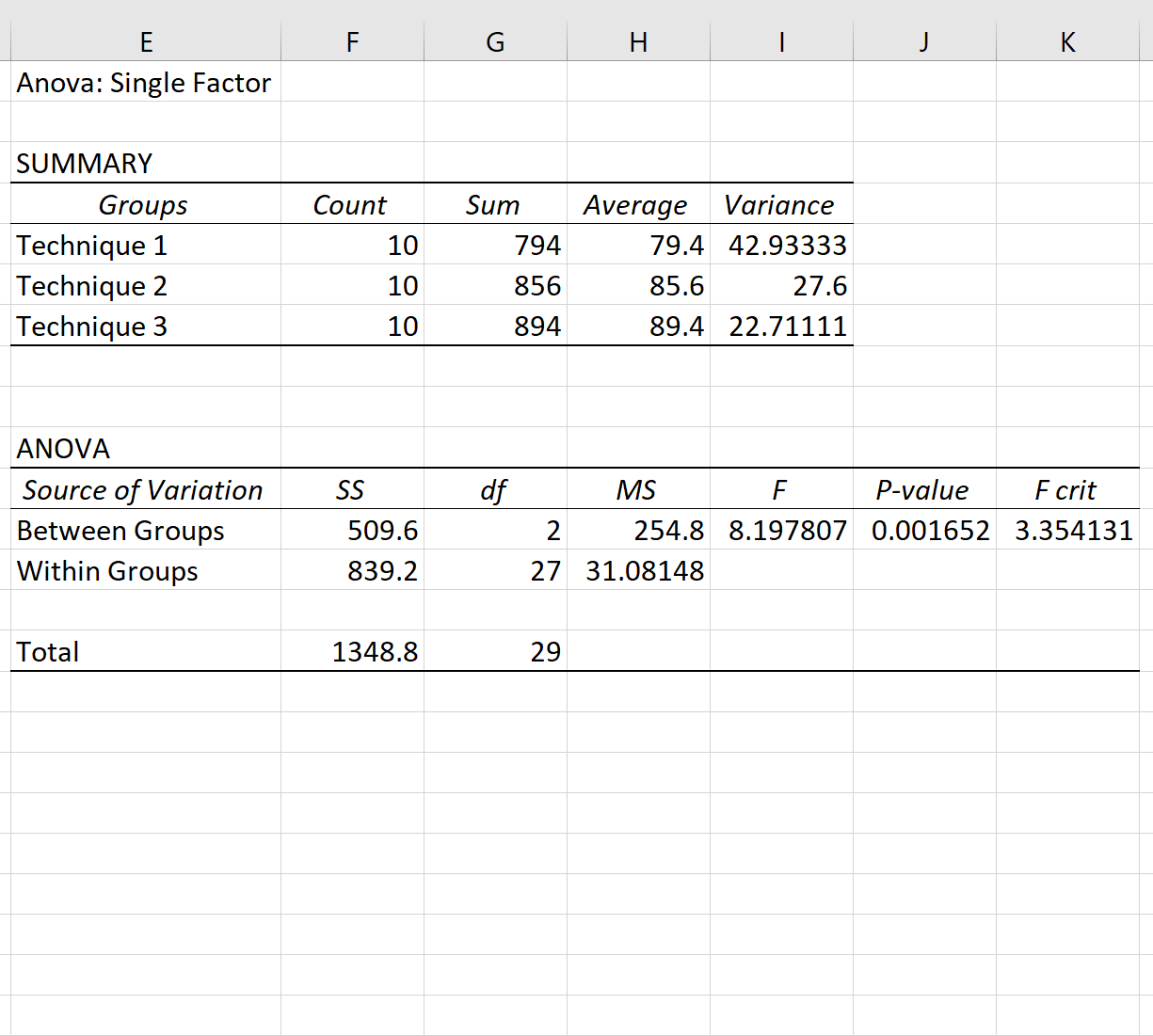
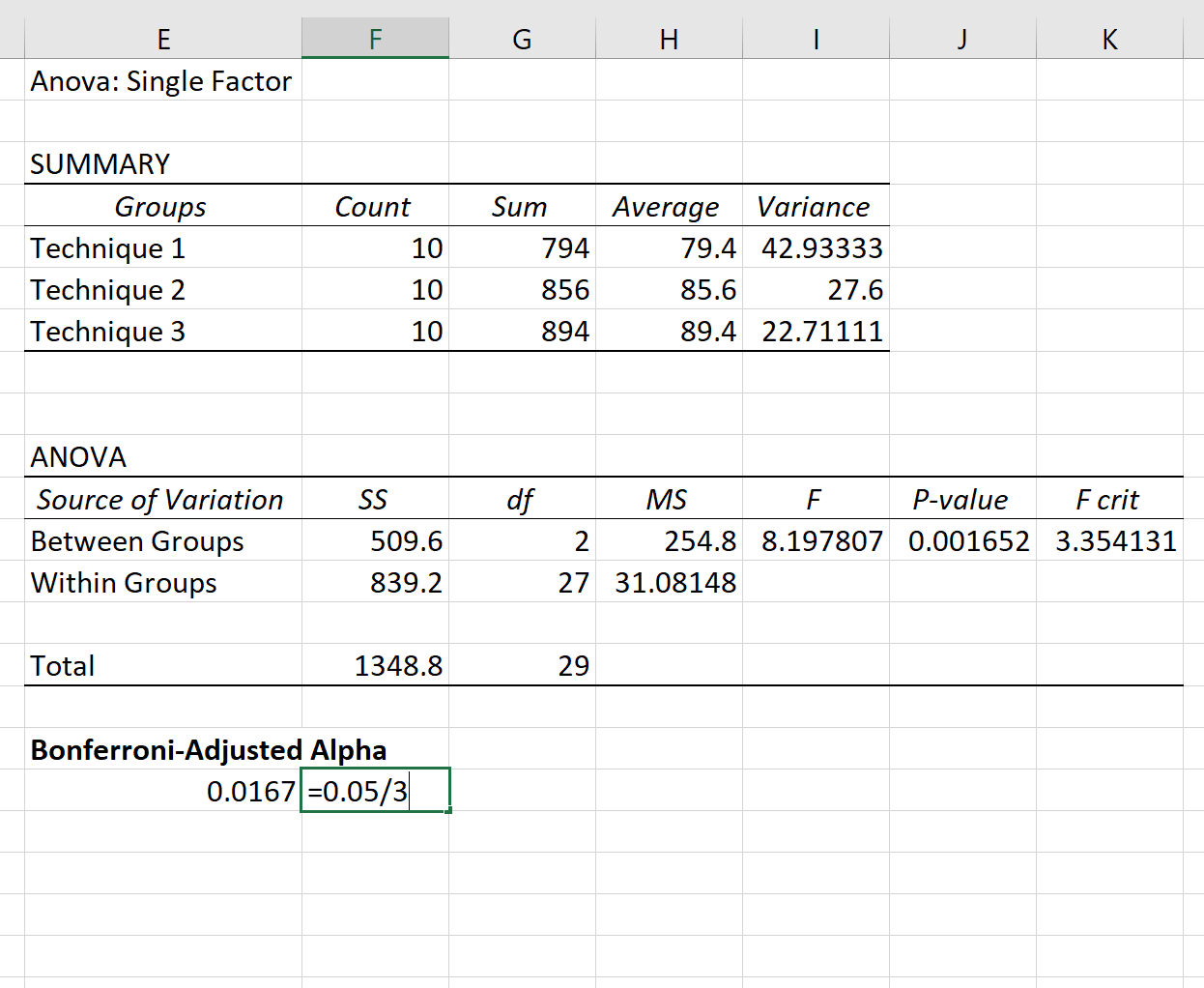
Les résultats de l’ANOVA unidirectionnelle apparaîtront automatiquement :
Rappelons qu’une ANOVA unidirectionnelle a les hypothèses nulles et alternatives suivantes :
- H 0 (hypothèse nulle) : toutes les moyennes des groupes sont égales.
- H A (hypothèse alternative) : Au moins une moyenne de groupe est différente du reste.
Étant donné que la valeur p dans le tableau ANOVA (0,001652) est inférieure à 0,05, nous disposons de preuves suffisantes pour rejeter l’hypothèse nulle. En d’autres termes, les résultats moyens aux examens entre les trois groupes ne sont pas égaux.
Ensuite, nous pouvons effectuer plusieurs comparaisons en utilisant une correction de Bonferroni entre les trois groupes pour voir exactement quelles moyennes de groupe sont différentes.
Étape 3 : effectuer plusieurs comparaisons à l’aide d’une correction de Bonferroni
En utilisant une correction de Bonferroni, nous pouvons calculer le niveau alpha ajusté comme suit :
α nouveau = α original / n
Dans notre exemple, nous effectuerons les trois comparaisons suivantes :
- Technique 1 contre Technique 2
- Technique 1 contre Technique 3
- Technique 2 contre Technique 3
Puisque nous voulons utiliser α = .05 pour chaque test, la correction de Bonferroni nous indique que nous devrions utiliser α new = .0167 .
Ensuite, nous utiliserons un test t pour comparer les moyennes entre chaque groupe. Dans Excel, on peut utiliser la syntaxe suivante :
=TTEST(Tableau1, Tableau2, queues=2, type=2)
où:
- Array1 : le premier tableau de données
- Array2 : le deuxième tableau de données
- tails : Le nombre de queues du test. Nous utiliserons « 2 » pour indiquer un test bilatéral.
- type : Le type de test t à effectuer. Nous utiliserons « 2 » pour indiquer un test t avec des variances égales.
La capture d’écran suivante montre comment effectuer chaque test t :
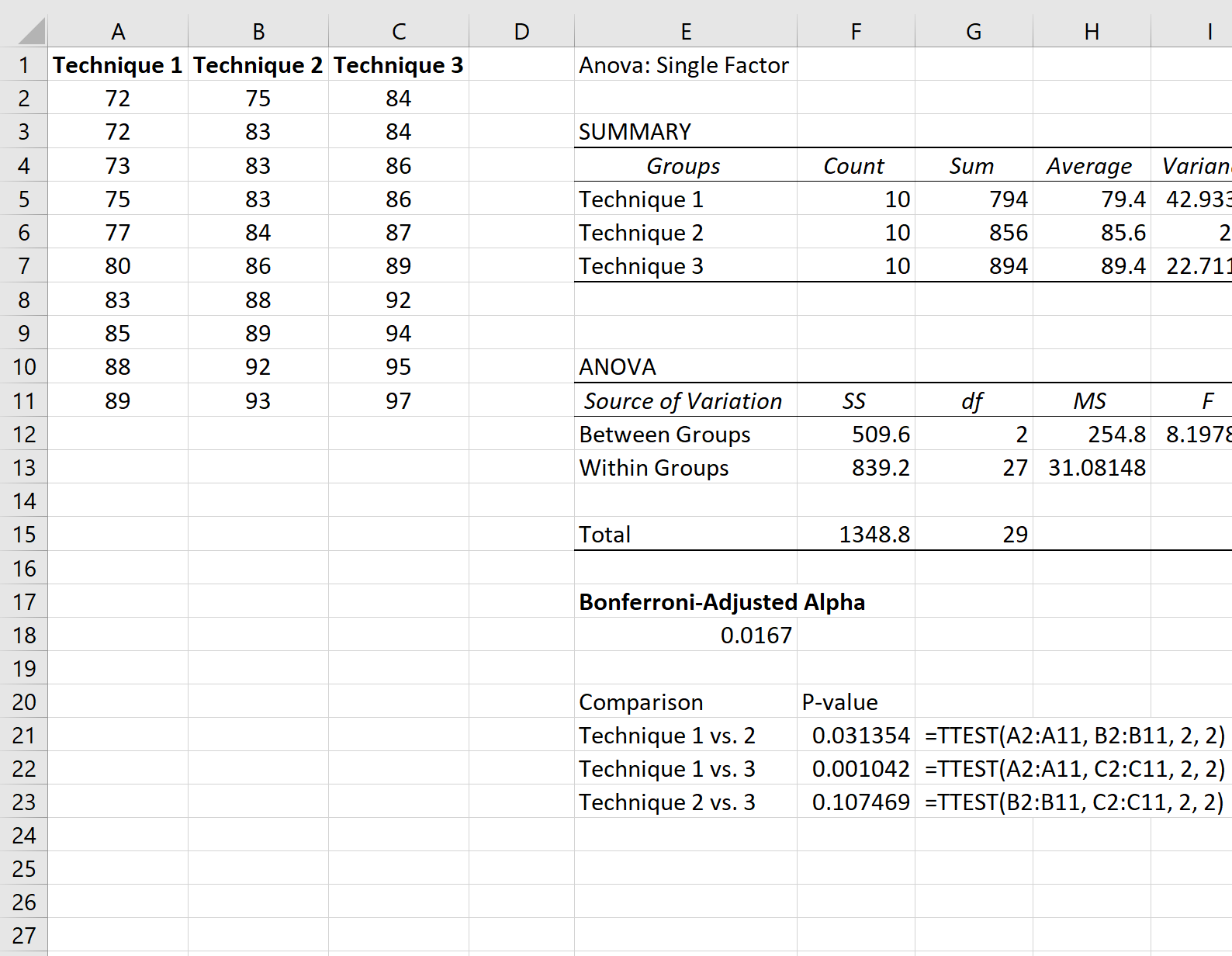
La seule valeur p inférieure au niveau alpha ajusté par Bonferroni provient de la comparaison entre la technique 1 et la technique 2, qui avait une valeur p de 0,001042 .
Ainsi, nous conclurions que seule la différence statistiquement significative dans les résultats moyens aux examens se situait entre la technique 1 et la technique 2.
Ressources additionnelles
Quel est le taux d’erreur par famille ?
La correction de Bonferroni : définition et exemple
Calculateur de correction Bonferroni
