La variance peut-elle être négative ?
En statistiques, le terme variance fait référence à la façon dont les valeurs sont réparties dans un ensemble de données donné.
Une question courante que les étudiants se posent à propos de la variance est la suivante :
La variance peut-elle être négative ?
La réponse : Non, la variance ne peut pas être négative. La valeur la plus basse qu’il puisse prendre est zéro.
Pour comprendre pourquoi c’est le cas, nous devons comprendre comment la variance est réellement calculée.
Comment calculer l’écart
La formule pour trouver la variance d’un échantillon (notée s 2 ) est :
s 2 = Σ (x je – x ) 2 / (n-1)
où:
- x : La moyenne de l’échantillon
- x i : La ième observation dans l’échantillon
- N : La taille de l’échantillon
- Σ : Un symbole grec qui signifie « somme »
Par exemple, supposons que nous ayons l’ensemble de données suivant avec 10 valeurs :
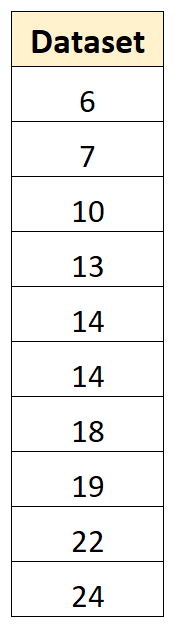
Nous pouvons utiliser les étapes suivantes pour calculer la variance de cet échantillon :
Étape 1 : Trouver la moyenne
La moyenne est simplement la moyenne. Cela s’avère être 14,7 .
Étape 2 : Trouver les écarts au carré
Ensuite, nous pouvons calculer l’écart carré de chaque valeur individuelle par rapport à la moyenne.
Par exemple, le premier écart carré est calculé comme (6-14,7) 2 = 75,69.
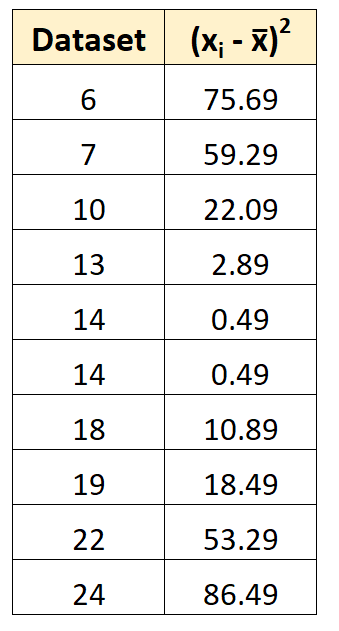
Étape 3 : Trouver la somme des écarts au carré
Ensuite, nous pouvons faire la somme de tous les carrés des écarts :
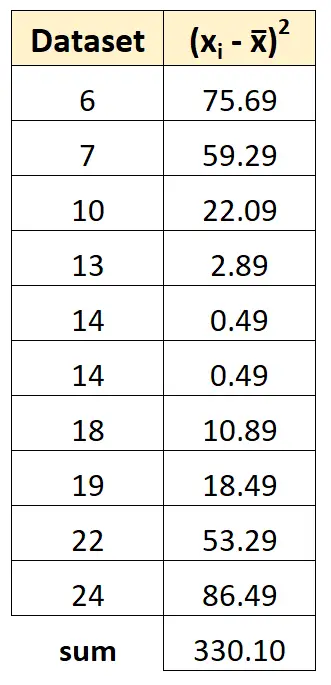
Étape 4 : Calculer la variance de l’échantillon
Enfin, nous pouvons calculer la variance de l’échantillon comme la somme des écarts carrés divisée par (n-1) :
s 2 = 330,1 / (10-1) = 330,1 / 9 = 36,678
La variance de l’échantillon s’avère être de 36,678 .
Un exemple de variance nulle
La seule façon pour un ensemble de données d’avoir une variance nulle est si toutes les valeurs de l’ensemble de données sont les mêmes .
Par exemple, l’ensemble de données suivant a une variance d’échantillon de zéro :
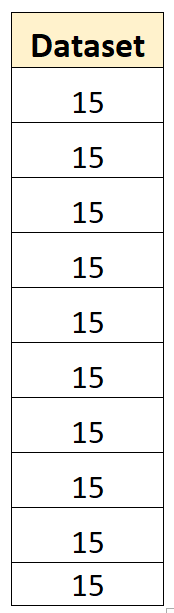
La moyenne de l’ensemble de données est de 15 et aucune des valeurs individuelles ne s’écarte de la moyenne. Ainsi, la somme des carrés des écarts sera nulle et la variance de l’échantillon sera simplement nulle.
L’écart type peut-il être négatif ?
Une manière plus courante de mesurer la répartition des valeurs dans un ensemble de données consiste à utiliser l’écart type, qui est simplement la racine carrée de la variance.
Par exemple, si la variance d’un échantillon donné est s 2 = 36,678 , alors l’écart type (écrit s ) est calculé comme suit :
s = √ s2 = √ 36,678 = 6,056
Puisque nous savons déjà que la variance est toujours nulle ou un nombre positif, cela signifie que l’écart type ne peut jamais être négatif puisque la racine carrée de zéro ou d’un nombre positif ne peut pas être négative.
Ressources additionnelles
Mesures de tendance centrale : définition et exemples
Mesures de dispersion : définition et exemples
