Qu’est-ce qu’une ANOVA Factorielle ? (Définition & #038; Exemple)

Une ANOVA factorielle est toute ANOVA (« analyse de variance ») qui utilise deux ou plusieurs facteurs indépendants et une seule variable de réponse.

Ce type d’ANOVA doit être utilisé chaque fois que vous souhaitez comprendre comment deux facteurs ou plus affectent une variable de réponse et s’il existe ou non un effet d’interaction entre les facteurs sur la variable de réponse.

Ce didacticiel fournit plusieurs exemples de situations dans lesquelles une ANOVA factorielle peut être utilisée, ainsi qu’un exemple étape par étape de la manière d’effectuer une ANOVA factorielle.

Remarque : Une ANOVA bidirectionnelle est un type d’ANOVA factorielle.

Exemples d’utilisation d’une ANOVA factorielle

Une ANOVA factorielle pourrait être utilisée dans chacune des situations suivantes.

Exemple 1 : Croissance des plantes

Un botaniste veut comprendre comment l’exposition au soleil et la fréquence d’arrosage affectent la croissance des plantes. Elle plante 100 graines et les laisse pousser pendant trois mois dans différentes conditions d’exposition au soleil et de fréquence d’arrosage. Au bout de trois mois, elle enregistre la hauteur de chaque plante.

Dans ce cas, elle a les variables suivantes :

• Variable de réponse : croissance des plantes
• Facteurs : exposition au soleil, fréquence d’arrosage

Et elle aimerait répondre aux questions suivantes :

• L’exposition au soleil affecte-t-elle la croissance des plantes ?
• La fréquence d’arrosage affecte-t-elle la croissance des plantes ?
• Existe-t-il un effet d’interaction entre l’exposition au soleil et la fréquence d’arrosage ?

Elle pourrait utiliser une ANOVA factorielle pour cette analyse car elle souhaite comprendre comment deux facteurs affectent une seule variable de réponse.

Exemple 2 : Résultats des examens

Un professeur souhaite comprendre comment le temps de cours et la méthode d’enseignement affectent les résultats des examens. Il utilise deux méthodes d’enseignement différentes et deux horaires d’enseignement différents (tôt le matin et début d’après-midi) et enregistre les notes moyennes aux examens de chaque étudiant à la fin du semestre.

Dans ce cas, il a les variables suivantes :

• Variable de réponse : score à l’examen
• Facteurs : méthode d’enseignement, temps d’enseignement

Et il aimerait répondre aux questions suivantes :

• La méthode d’enseignement affecte-t-elle les résultats aux examens ?
• Le temps d’enseignement affecte-t-il les résultats aux examens ?
• Existe-t-il un effet d’interaction entre la méthode d’enseignement et le temps d’enseignement ?

Il pourrait utiliser une ANOVA factorielle pour cette analyse car il souhaite comprendre comment deux facteurs affectent une seule variable de réponse.

Exemple 3 : Revenu annuel

Un économiste collecte des données pour comprendre comment le niveau d’éducation (diplôme d’études secondaires, diplôme collégial, diplôme d’études supérieures), l’état civil (célibataire, divorcé, marié) et la région (Nord, Est, Sud, Ouest) affectent le revenu annuel.

Dans ce cas, il a les variables suivantes :

• Variable de réponse : revenu annuel
• Facteurs : niveau d’éducation, état civil, région

Et il aimerait répondre aux questions suivantes :

• Le niveau d’éducation affecte-t-il le revenu ?
• La situation matrimoniale affecte-t-elle les revenus ?
• La région affecte-t-elle les revenus ?
• Existe-t-il un effet d’interaction entre ces trois facteurs indépendants ?

Il pourrait utiliser une ANOVA factorielle pour cette analyse car il souhaite comprendre comment trois facteurs affectent une seule variable de réponse.

Exemple étape par étape d’une ANOVA factorielle

Un botaniste veut savoir si l’exposition au soleil et la fréquence des arrosages affectent la croissance des plantes. Elle plante 40 graines et les laisse pousser pendant deux mois dans différentes conditions d’exposition au soleil et de fréquence d’arrosage. Au bout de deux mois, elle enregistre la hauteur de chaque plante.

Les résultats sont montrés plus bas:

Nous pouvons voir que cinq plantes ont été cultivées dans chaque combinaison de conditions.

Par exemple, cinq plantes ont été cultivées avec un arrosage quotidien et sans lumière du soleil et leurs hauteurs après deux mois étaient de 4,8 pouces, 4,4 pouces, 3,2 pouces, 3,9 pouces et 4,4 pouces :

Le botaniste utilise ces données pour effectuer une ANOVA factorielle dans Excel et obtient le résultat suivant :

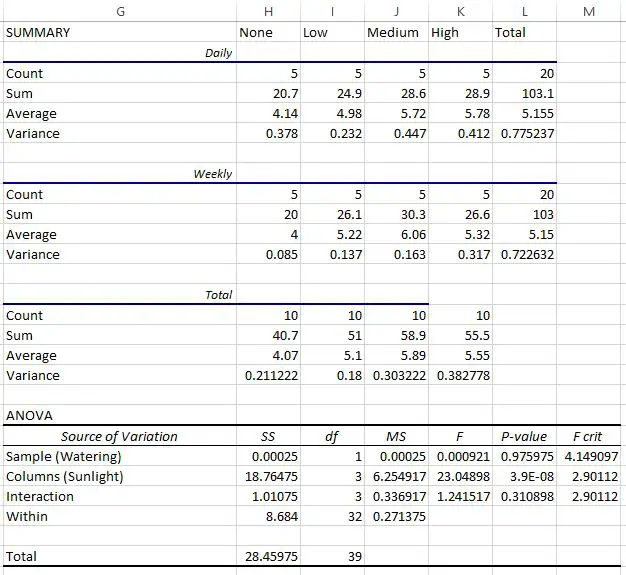
Le dernier tableau montre le résultat de l’ANOVA factorielle :

• La valeur p pour l’interaction entre la fréquence d’arrosage et l’exposition au soleil était de 0,310898 . Ceci n’est pas statistiquement significatif au niveau alpha de 0,05.
• La valeur p pour la fréquence d’arrosage était de 0,975975 . Ceci n’est pas statistiquement significatif au niveau alpha de 0,05.
• La valeur p pour l’exposition au soleil était de 3,9E-8 (0,000000039) . Ceci est statistiquement significatif au niveau alpha de 0,05.

Nous pouvons conclure que l’exposition au soleil est le seul facteur ayant un effet statistiquement significatif sur la croissance des plantes.

Nous pouvons également conclure qu’il n’y a pas d’effet d’interaction entre l’exposition au soleil et la fréquence d’arrosage et que la fréquence d’arrosage n’a pas d’effet statistiquement significatif sur la croissance des plantes.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les modèles ANOVA :

Une introduction à l’ANOVA unidirectionnelle
Une introduction à l’ANOVA bidirectionnelle
Une introduction à l’ANOVA à mesures répétées
Les différences entre ANOVA, ANCOVA, MANOVA et MANCOVA