Une introduction à la distribution exponentielle

La distribution exponentielle est une distribution de probabilité utilisée pour modéliser le temps que nous devons attendre jusqu’à ce qu’un certain événement se produise.

Cette distribution peut être utilisée pour répondre à des questions telles que :

• Combien de temps un commerçant doit-il attendre qu’un client entre dans son magasin ?
• Combien de temps un ordinateur portable continuera-t-il à fonctionner avant de tomber en panne ?
• Combien de temps une batterie de voiture continuera-t-elle à fonctionner avant de mourir ?
• Combien de temps devons-nous attendre jusqu’à la prochaine éruption volcanique dans une certaine région ?

Dans chaque scénario, nous souhaitons calculer combien de temps nous devrons attendre jusqu’à ce qu’un certain événement se produise. Ainsi, chaque scénario pourrait être modélisé à l’aide d’une distribution exponentielle.

Distribution exponentielle : PDF et CDF

Si une variable aléatoire X suit une distribution exponentielle, alors la fonction de densité de probabilité de X peut s’écrire :

f (x; λ) = λe ^-λx

où:

• λ : le paramètre de taux (calculé comme λ = 1/μ)
• e : Une constante à peu près égale à 2,718

La fonction de distribution cumulative de X peut s’écrire :

F (x; λ) = 1 – e ^-λx

En pratique, le CDF est le plus souvent utilisé pour calculer des probabilités liées à la distribution exponentielle.

Par exemple, supposons que le nombre moyen de minutes entre les éruptions d’un certain geyser soit de 40 minutes. Quelle est la probabilité que nous devions attendre moins de 50 minutes pour une éruption ?

Pour résoudre ce problème, nous devons d’abord calculer le paramètre de taux :

• λ = 1/µ
• λ = 1/40
• λ = 0,025

Nous pouvons brancher λ = 0,025 et x = 50 à la formule du CDF :

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

La probabilité que nous devions attendre moins de 50 minutes pour la prochaine éruption est de 0,7135 .

Visualiser la distribution exponentielle

Le graphique suivant montre la fonction de densité de probabilité d’une variable aléatoire X qui suit une distribution exponentielle avec différents paramètres de taux :

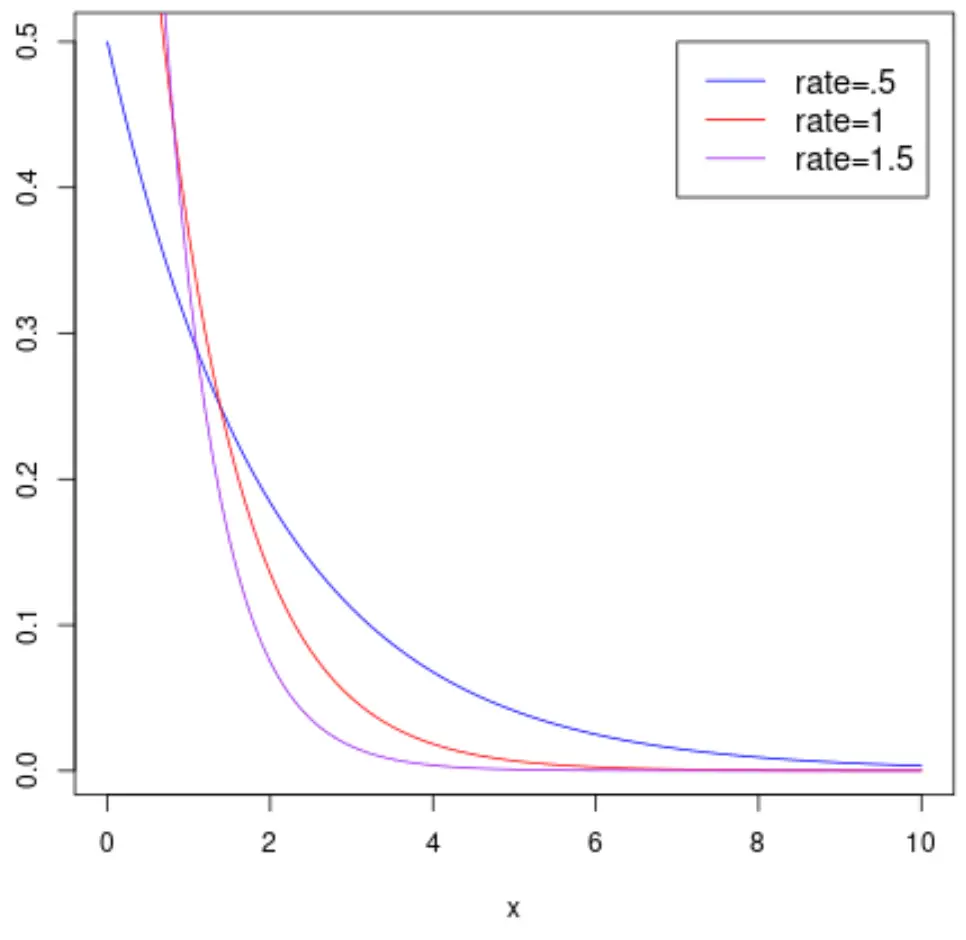
Et le graphique suivant montre la fonction de distribution cumulative d’une variable aléatoire X qui suit une distribution exponentielle avec différents paramètres de taux :

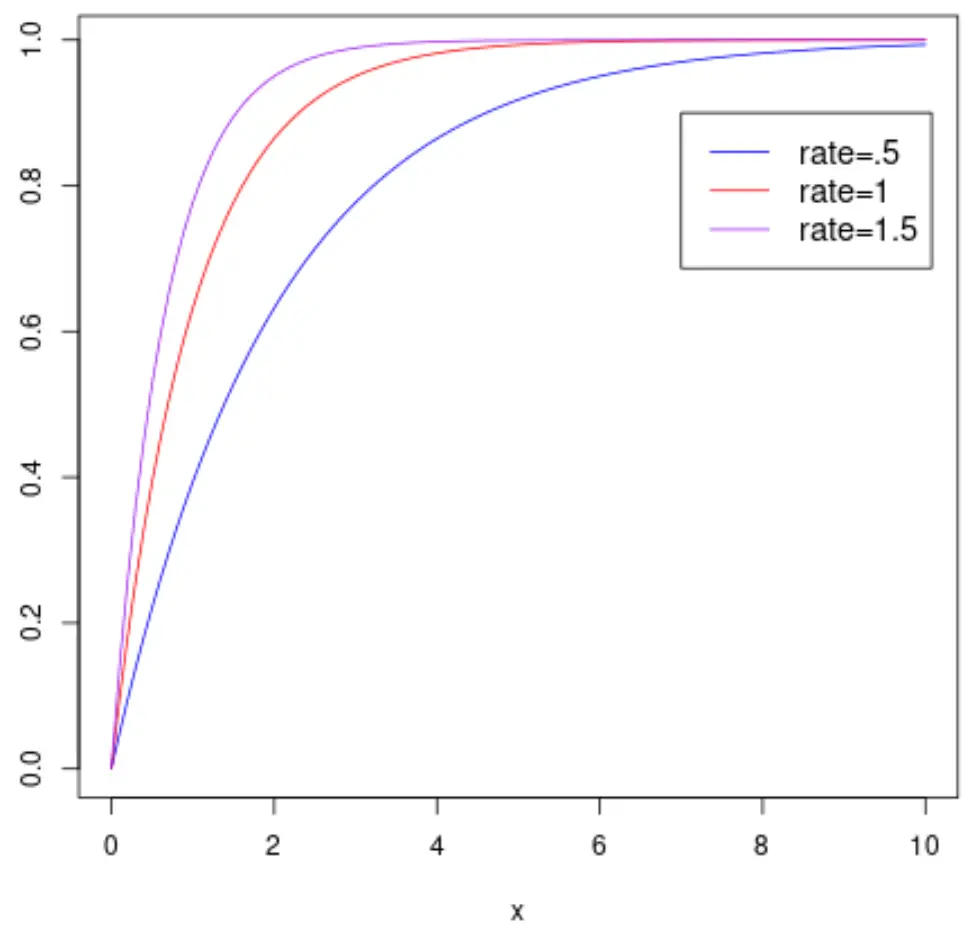
Remarque : Consultez ce didacticiel pour savoir comment tracer une distribution exponentielle dans R.

Propriétés de la distribution exponentielle

La distribution exponentielle a les propriétés suivantes :

• Moyenne : 1 / λ
• Écart : 1 / λ ²

Par exemple, supposons que le nombre moyen de minutes entre les éruptions d’un certain geyser soit de 40 minutes. Nous calculerions le taux comme λ = 1/μ = 1/40 = 0,025.

Nous pourrions alors calculer les propriétés suivantes pour cette distribution :

• Temps d’attente moyen pour la prochaine éruption : 1/λ = 1 /.025 = 40
• Variation des délais d’attente pour la prochaine éruption : 1/λ ² = 1 /.025 ² = 1600

Remarque : La distribution exponentielle possède également une propriété sans mémoire , ce qui signifie que la probabilité qu’un événement futur se produise n’est pas affectée par l’occurrence d’événements passés.

Problèmes de pratique de distribution exponentielle

Utilisez les problèmes pratiques suivants pour tester vos connaissances sur la distribution exponentielle.

Question 1 : Un nouveau client entre dans un magasin toutes les deux minutes en moyenne. Après l’arrivée d’un client, déterminez la probabilité qu’un nouveau client arrive en moins d’une minute.

Solution 1 : Le délai moyen entre les clients est de deux minutes. Ainsi, le taux peut être calculé comme suit :

• λ = 1/µ
• λ = 1/2
• λ = 0,5

Nous pouvons brancher λ = 0,5 et x = 1 à la formule du CDF :

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,5(1)
• P(X ≤ 1) = 0,3935

La probabilité que nous devions attendre moins d’une minute pour l’arrivée du prochain client est de 0,3935 .

Question 2 : Un tremblement de terre se produit en moyenne tous les 400 jours dans une certaine région. Après un tremblement de terre, déterminez la probabilité qu’il faudra plus de 500 jours avant que le prochain tremblement de terre ne se produise.

Solution 2 : Le délai moyen entre les tremblements de terre est de 400 jours. Ainsi, le taux peut être calculé comme suit :

• λ = 1/µ
• λ = 1/400
• λ = 0,0025

Nous pouvons brancher λ = 0,0025 et x = 500 à la formule du CDF :

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,0025(500)
• P(X ≤ 1) = 0,7135

La probabilité que nous devions attendre moins de 500 jours pour le prochain séisme est de 0,7135. Ainsi, la probabilité que nous devions attendre plus de 500 jours pour le prochain tremblement de terre est de 1 – 0,7135 = 0,2865 .

Question 3 : Un centre d’appels reçoit un nouvel appel toutes les 10 minutes en moyenne. Après qu’un client appelle, déterminez la probabilité qu’un nouveau client appelle dans les 10 à 15 minutes.

Solution 3 : Le temps moyen entre les appels est de 10 minutes. Ainsi, le taux peut être calculé comme suit :

• λ = 1/µ
• λ = 1/10
• λ = 0,1

Nous pouvons utiliser la formule suivante pour calculer la probabilité qu’un nouveau client appelle dans les 10 à 15 minutes :

• P(10 < X ≤ 15) = (1 – e ^-0,1(15) ) – (1 – e ^-0,1(10) )
• P(10 < X ≤ 15) = 0,7769 – 0,6321
• P(10 < X ≤ 15) = 0,1448

La probabilité qu’un nouveau client appelle dans les 10 à 15 minutes. est 0,1448 .

Ressources additionnelles

Les didacticiels suivants fournissent des introductions à d’autres distributions de probabilité courantes.

Une introduction à la distribution normale
Une introduction à la distribution binomiale
Une introduction à la distribution de Poisson
Une introduction à la distribution uniforme