Qu’est-ce que la fiabilité des formulaires parallèles ? (Définition & #038; Exemple)

En statistique, la fiabilité des formes parallèles mesure la corrélation entre deux formes équivalentes d’un test.

Le processus de calcul de la fiabilité des formulaires parallèles est le suivant :

Étape 1 : divisez un test en deux.

Par exemple, divisez au hasard un test de 100 questions en un test A contenant 50 questions et un test B contenant également 50 questions.

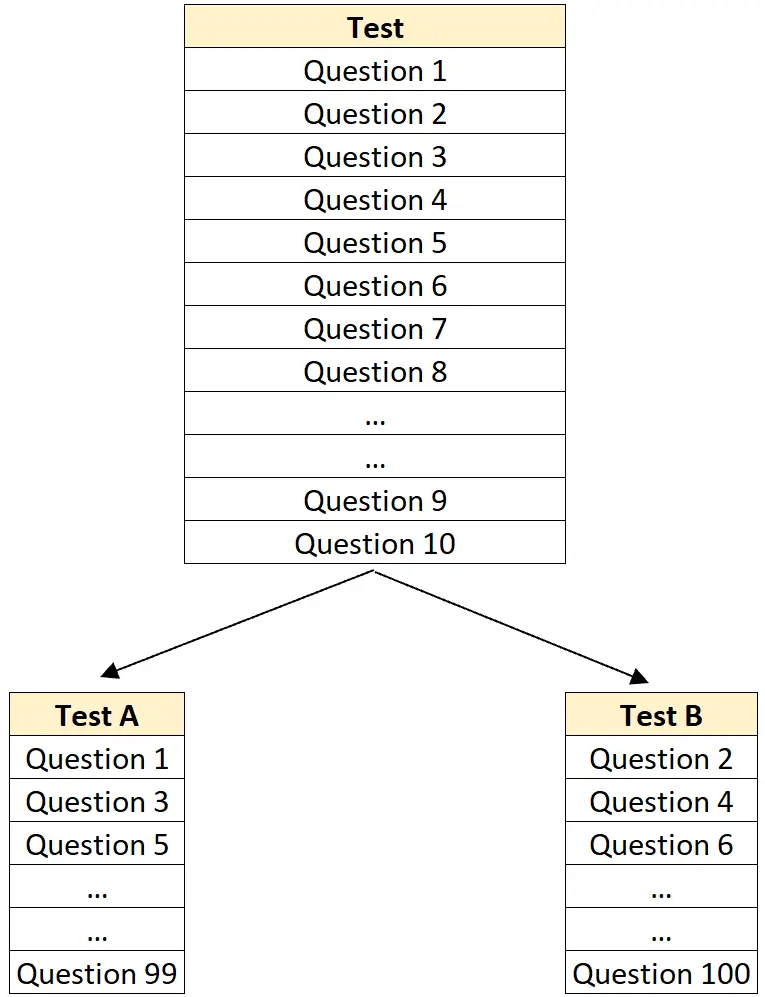
Étape 2 : Administrez la première moitié à tous les étudiants, puis administrez la seconde moitié à tous les étudiants.

Par exemple, administrez le test A aux 20 élèves d’une certaine classe et enregistrez leurs scores. Ensuite, peut-être un mois plus tard, administrez le test B aux mêmes 20 étudiants et enregistrez également leurs résultats à ce test.

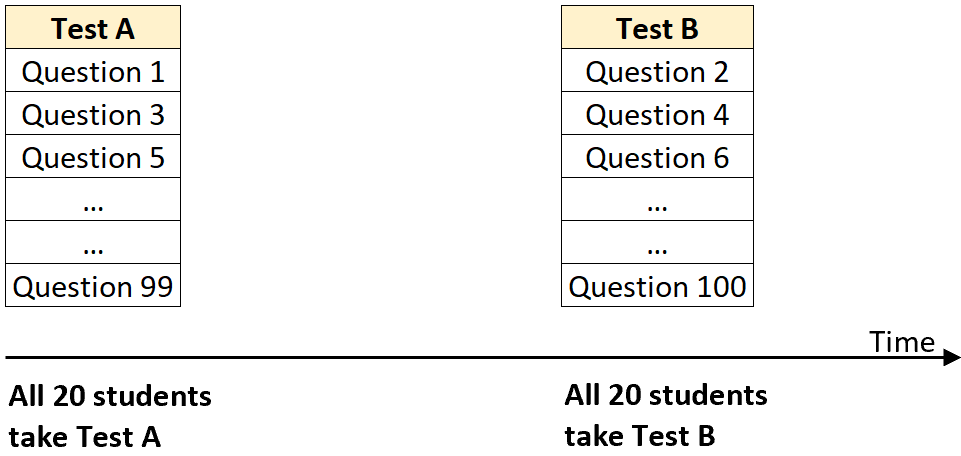
Étape 3 : Calculez la corrélation entre les résultats des tests pour les deux tests.

Calculez la corrélation entre les scores des deux tests. On dit qu’un test a une fiabilité de formes parallèles si la corrélation entre les scores est élevée.

Quand utiliser la fiabilité des formulaires parallèles

La fiabilité des formulaires parallèles est souvent utilisée dans le cadre académique lorsqu’un professeur ne souhaite pas que les étudiants puissent avoir accès aux questions du test à l’avance.

Par exemple, si le professeur distribue le test A à tous les étudiants au début du semestre, puis distribue le même test A à la fin du semestre, les étudiants peuvent simplement mémoriser les questions et réponses du premier test.

Cependant, en distribuant un test B différent à la fin du semestre (et, espérons-le, de difficulté égale), le professeur est en mesure d’évaluer les connaissances des étudiants tout en garantissant que les étudiants n’ont pas vu les questions auparavant.

Inconvénients potentiels de la fiabilité des formes parallèles

La fiabilité des formulaires parallèles présente deux inconvénients potentiels :

1. Cela nécessite beaucoup de questions.

La fiabilité des formes parallèles fonctionne mieux pour les tests comportant un grand nombre de questions (par exemple 100 questions), car le nombre que nous calculons pour la corrélation sera plus fiable.

2. Il n’y a aucune garantie que les deux moitiés soient réellement parallèles.

Lorsque nous divisons aléatoirement un test en deux moitiés, rien ne garantit que les deux moitiés seront réellement parallèles ou « égales » en difficulté. Cela signifie que les scores peuvent différer entre les deux tests simplement parce qu’une moitié s’avère plus difficile que l’autre.

Fiabilité des formulaires parallèles et fiabilité divisée en deux

La fiabilité des formulaires parallèles est similaire à la fiabilité divisée en deux , mais il existe une légère différence :

Fiabilité divisée en deux :

Cela implique de diviser un test en deux moitiés et d’administrer chaque moitié au même groupe d’étudiants. L’ordre dans lequel les étudiants passent le test n’a pas d’importance.

L’intérêt de cette méthode est de mesurer la cohérence interne . Idéalement, nous aimerions que la corrélation entre les moitiés soit élevée, car cela indique que toutes les parties du test contribuent de manière égale à ce qui est mesuré.

Fiabilité des formulaires parallèles :

Cela implique de diviser un test en deux moitiés – appelez-les « A » et « B » – et d’administrer chaque moitié au même groupe d’étudiants.

Cependant, il est important que tous les élèves passent d’abord le test « A », puis le test « B », afin que connaître les réponses au test « A » n’apporte aucun avantage aux élèves qui passeront plus tard le test « B ».

Ressources additionnelles

Une introduction rapide à l’analyse de fiabilité
Qu’est-ce que la fiabilité divisée en deux ?
Qu’est-ce que la fiabilité test-retest ?
Qu’est-ce que la fiabilité inter-évaluateurs ?