Comment calculer les probabilités NormalCDF dans Excel

La fonction NormalCDF sur une calculatrice TI-83 ou TI-84 peut être utilisée pour trouver la probabilité qu’une variable aléatoire normalement distribuée prenne une valeur dans une certaine plage.

Sur une calculatrice TI-83 ou TI-84, cette fonction utilise la syntaxe suivante

normalcdf (inférieur, supérieur, μ, σ)

où:

• inférieur = valeur inférieure de la plage
• supérieur = valeur supérieure de la plage
• μ = moyenne de la population
• σ = écart type de la population

Par exemple, supposons qu’une variable aléatoire soit normalement distribuée avec une moyenne de 50 et un écart type de 4. La probabilité qu’une variable aléatoire prenne une valeur comprise entre 48 et 52 peut être calculée comme suit :

normalcdf(48, 52, 50, 4) = 0,3829

Nous pouvons reproduire cette réponse dans Excel en utilisant la fonction NORM.DIST() , qui utilise la syntaxe suivante :

NORM.DIST(x, σ, μ, cumulatif)

où:

• x = valeur de donnée individuelle
• μ = moyenne de la population
• σ = écart type de la population
• cumulatif = FAUX calculer le PDF ; TRUE calcule le CDF

Les exemples suivants montrent comment utiliser cette fonction dans la pratique.

Exemple 1 : Probabilité entre deux valeurs

Supposons qu’une variable aléatoire soit normalement distribuée avec une moyenne de 50 et un écart type de 4. La probabilité qu’une variable aléatoire prenne une valeur comprise entre 48 et 52 peut être calculée comme suit :

=NORM.DIST(52, 50, 4, TRUE) - NORM.DIST(48, 50, 4, TRUE)

L’image suivante montre comment effectuer ce calcul dans Excel :

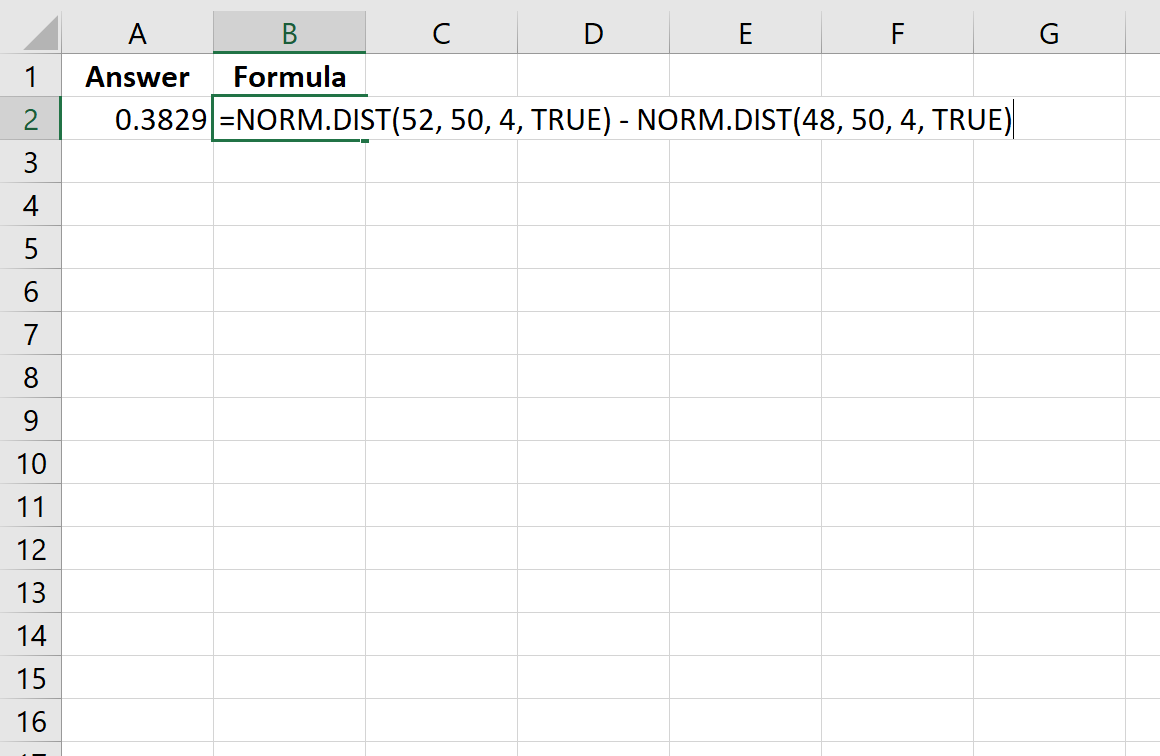
La probabilité s’avère être de 0,3829.

Exemple 2 : Probabilité inférieure à une valeur

Supposons qu’une variable aléatoire soit normalement distribuée avec une moyenne de 50 et un écart type de 4. La probabilité qu’une variable aléatoire prenne une valeur inférieure à 48 peut être calculée comme suit :

=NORM.DIST(48, 50, 4, TRUE)

L’image suivante montre comment effectuer ce calcul dans Excel :

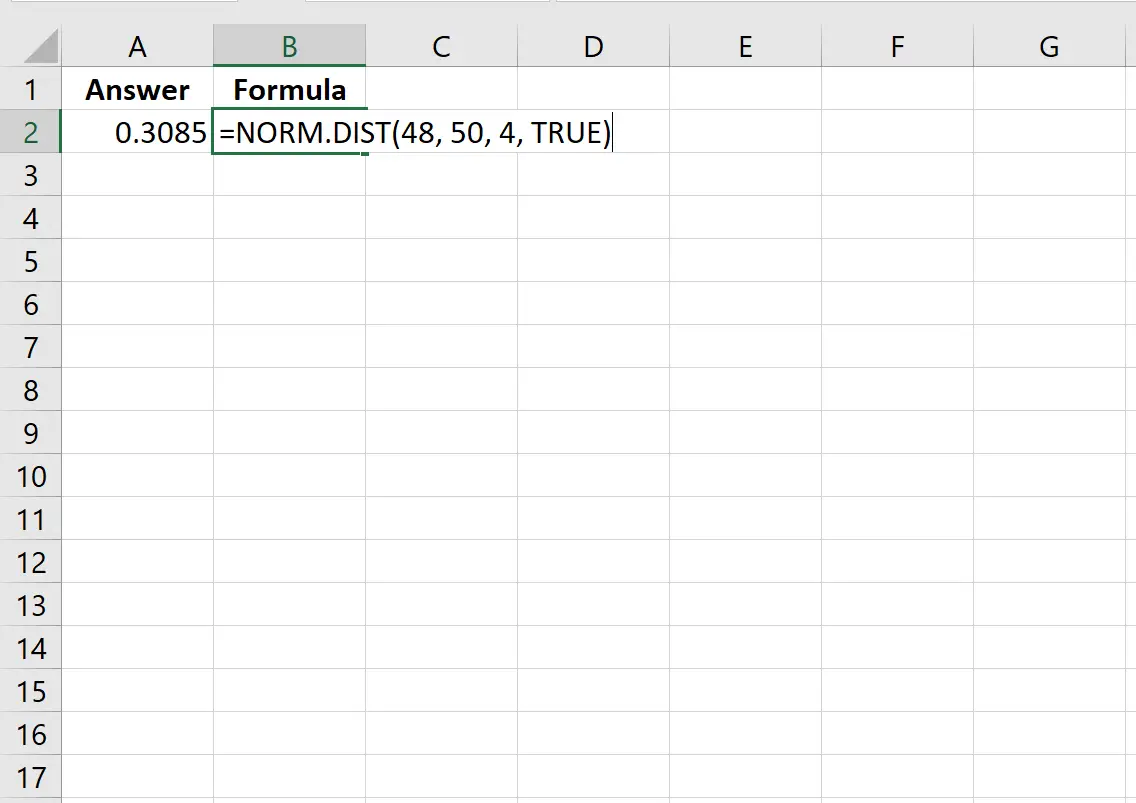
La probabilité s’avère être de 0,3085.

Exemple 3 : Probabilité supérieure à une valeur

Supposons qu’une variable aléatoire soit normalement distribuée avec une moyenne de 50 et un écart type de 4. La probabilité qu’une variable aléatoire prenne une valeur supérieure à 55 peut être calculée comme suit :

=1 - NORM.DIST(55, 50, 4, TRUE)

L’image suivante montre comment effectuer ce calcul dans Excel :

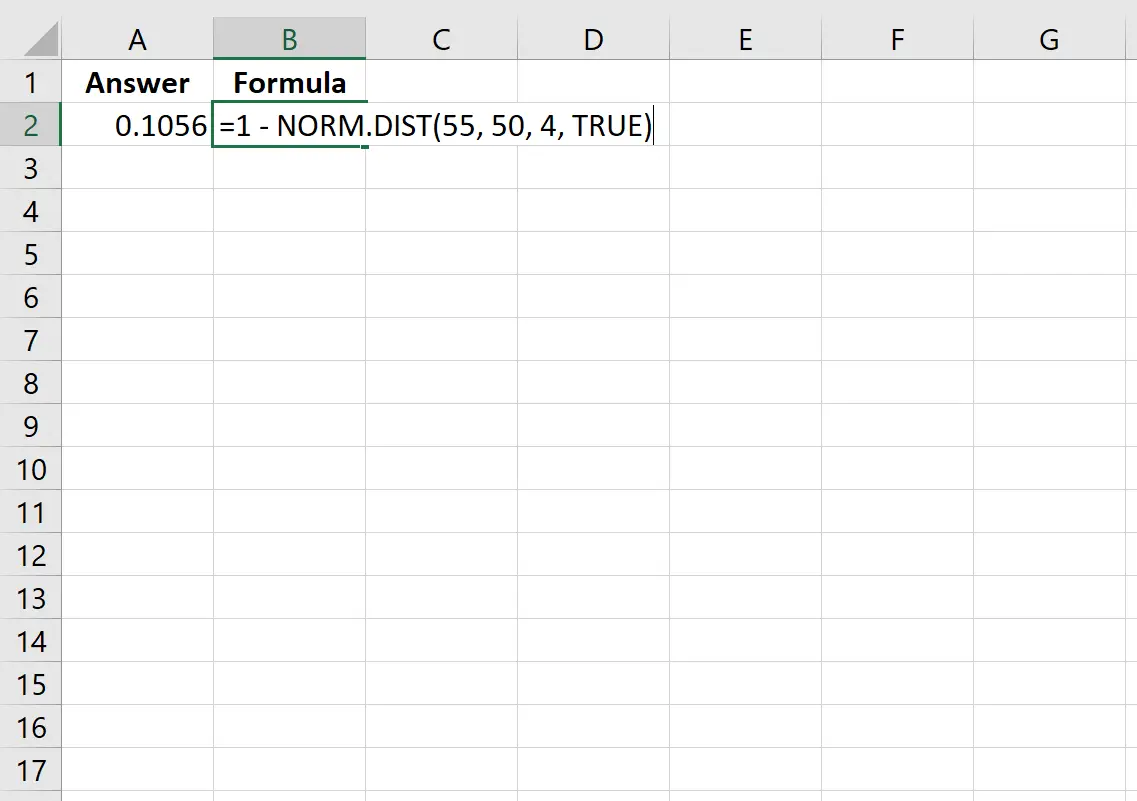
La probabilité s’avère être de 0,1056.

Ressources additionnelles

Vous pouvez également utiliser ce calculateur CDF normal pour rechercher automatiquement les probabilités associées à une distribution normale.