Comment effectuer un test de manque d’ajustement dans R (étape par étape)
Un test de manque d’ajustement est utilisé pour déterminer si un modèle de régression complet offre ou non un ajustement nettement meilleur à un ensemble de données qu’une version réduite du modèle.
Par exemple, supposons que nous souhaitions utiliser le nombre d’heures étudiées pour prédire les résultats aux examens des étudiants d’un certain collège. Nous pouvons décider d’adapter les deux modèles de régression suivants :
Modèle complet : score = β 0 + B 1 (heures) + B 2 (heures) 2
Modèle réduit : score = β 0 + B 1 (heures)
L’exemple étape par étape suivant montre comment effectuer un test de manque d’ajustement dans R pour déterminer si le modèle complet offre un ajustement nettement meilleur que le modèle réduit.
Étape 1 : Créer et visualiser un ensemble de données
Tout d’abord, nous allons utiliser le code suivant pour créer un ensemble de données contenant le nombre d’heures étudiées et les notes d’examen obtenues pour 50 étudiants :
#make this example reproducible set.seed(1) #create dataset df <- data.frame(hours = runif(50, 5, 15), score=50) df$score = df$score + df$hours^3/150 + df$hours*runif(50, 1, 2) #view first six rows of data head(df) hours score 1 7.655087 64.30191 2 8.721239 70.65430 3 10.728534 73.66114 4 14.082078 86.14630 5 7.016819 59.81595 6 13.983897 83.60510
Ensuite, nous allons créer un nuage de points pour visualiser la relation entre les heures et le score :
#load ggplot2 visualization package library(ggplot2) #create scatterplot ggplot(df, aes(x=hours, y=score)) + geom_point()
Étape 2 : Ajuster deux modèles différents à l’ensemble de données
Ensuite, nous adapterons deux modèles de régression différents à l’ensemble de données :
#fit full model full <- lm(score ~ poly(hours,2), data=df) #fit reduced model reduced <- lm(score ~ hours, data=df)
Étape 3 : Effectuer un test de manque d’ajustement
Ensuite, nous utiliserons la commande anova() pour effectuer un test de manque d’ajustement entre les deux modèles :
#lack of fit test
anova(full, reduced)
Analysis of Variance Table
Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 368.48
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
La statistique du test F s’avère être de 10,554 et la valeur p correspondante est de 0,002144 . Puisque cette valeur p est inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle du test et conclure que le modèle complet offre un ajustement statistiquement significativement meilleur que le modèle réduit.
Étape 4 : Visualisez le modèle final
Enfin, nous pouvons visualiser le modèle final (le modèle complet) par rapport à l’ensemble de données d’origine :
ggplot(df, aes(x=hours, y=score)) +
geom_point() +
stat_smooth(method='lm', formula = y ~ poly(x,2), size = 1) +
xlab('Hours Studied') +
ylab('Score')
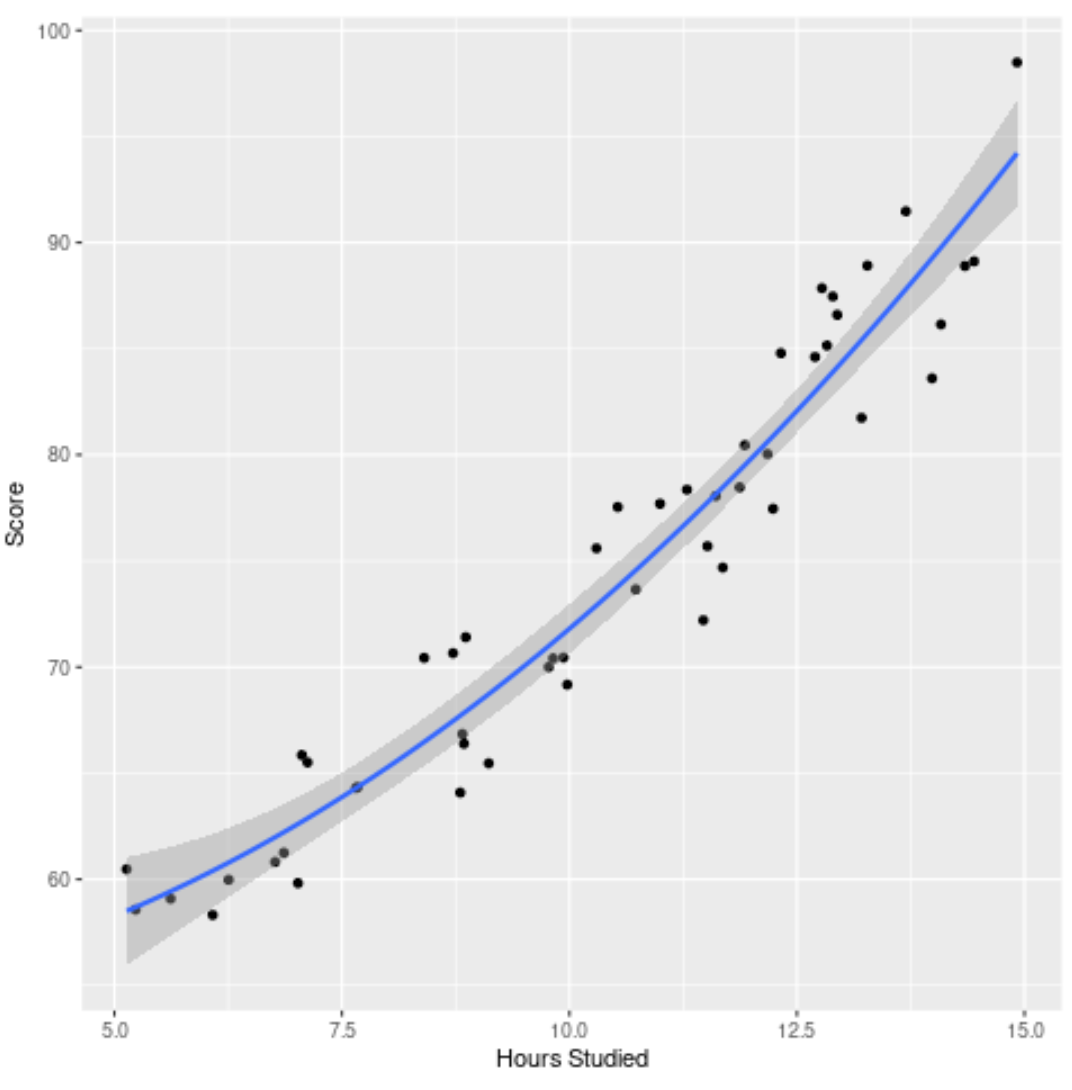
Nous pouvons voir que la courbe du modèle s’ajuste assez bien aux données.
Ressources additionnelles
Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression polynomiale dans R
