Ajustement de courbe dans Excel (avec exemples)
Souvent, vous souhaiterez peut-être trouver l’équation qui correspond le mieux à une courbe pour un ensemble de données dans Excel.
Heureusement, cela est assez simple à faire en utilisant la fonction Trendline d’Excel.
Ce didacticiel fournit un exemple étape par étape de la façon d’ajuster une équation à une courbe dans Excel.
Étape 1 : Créer les données
Tout d’abord, créons un faux ensemble de données avec lequel travailler :
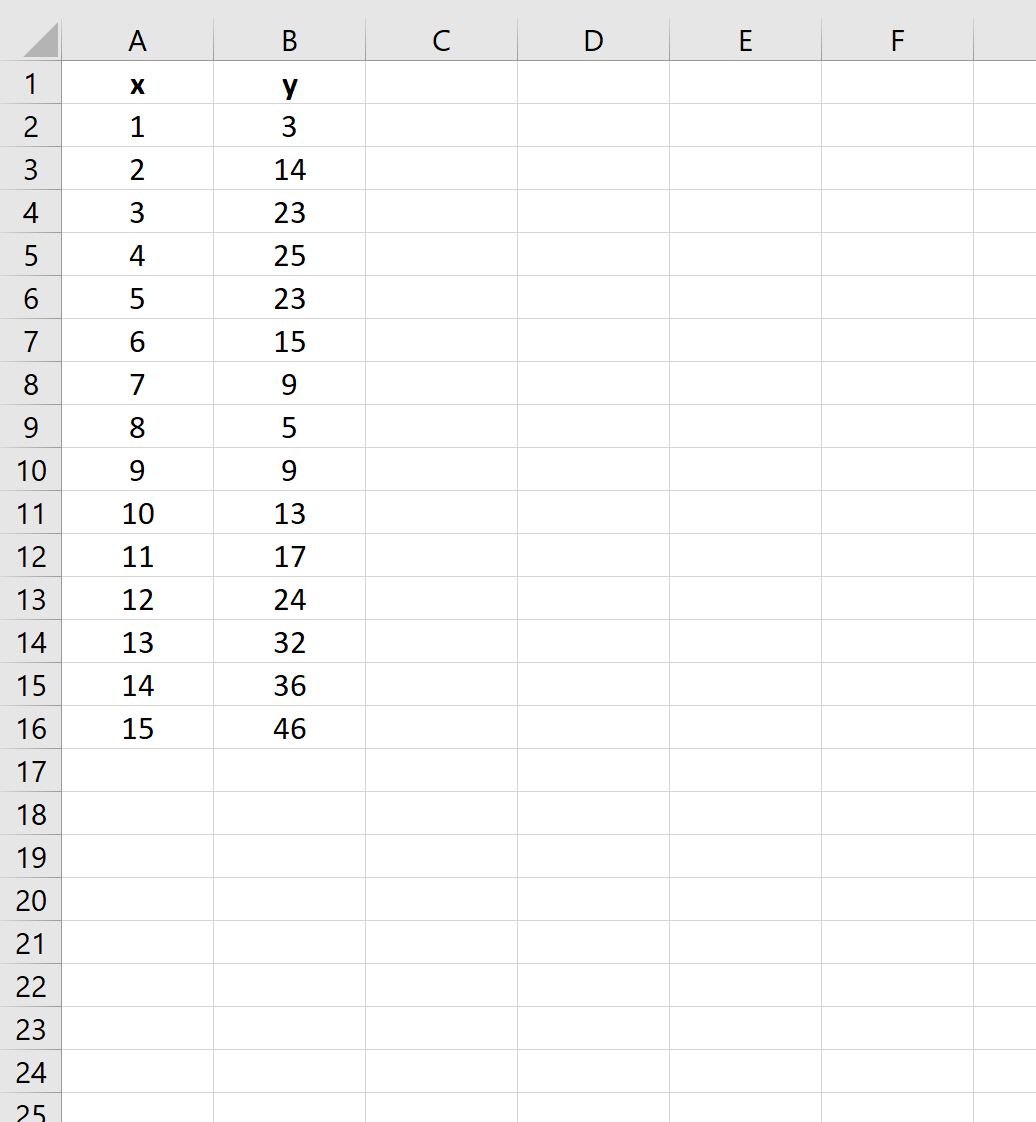
Étape 2 : Créer un nuage de points
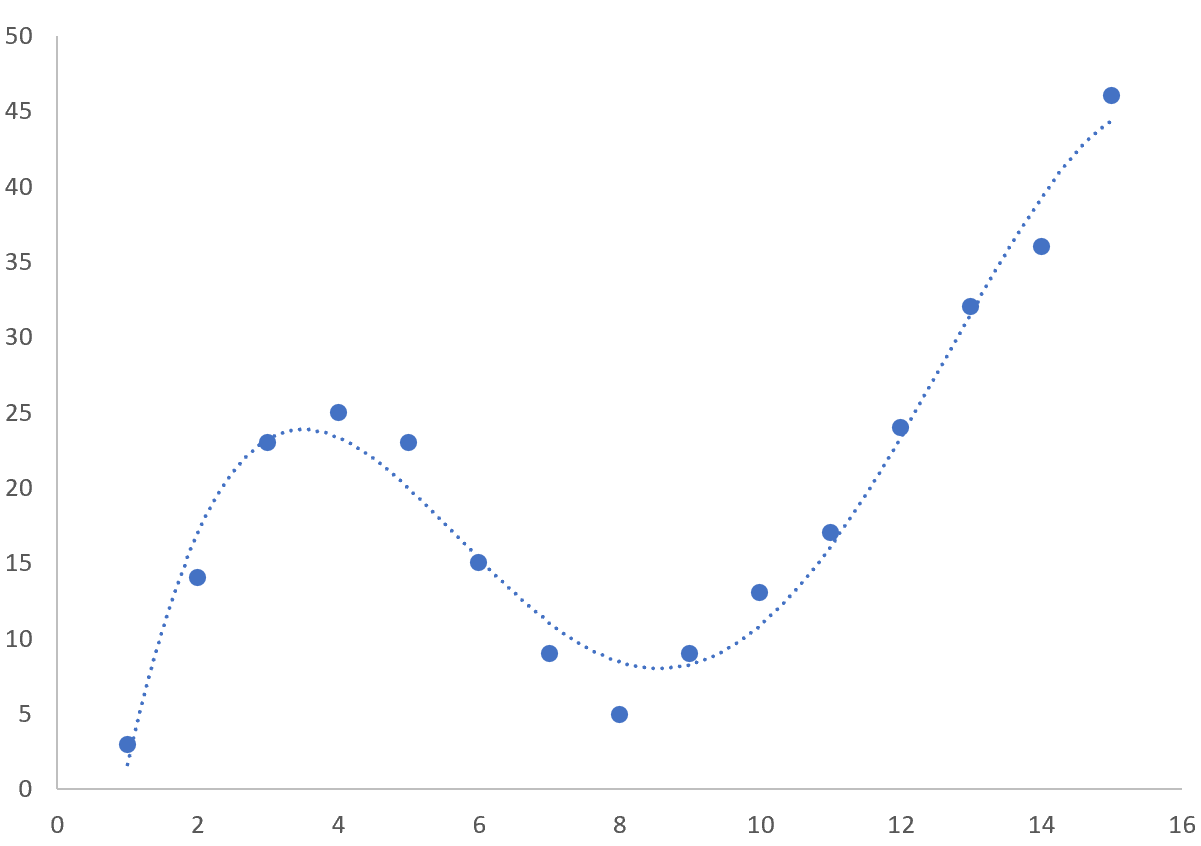
Créons ensuite un nuage de points pour visualiser l’ensemble de données.
Tout d’abord, mettez en surbrillance les cellules A2:B16 comme suit :
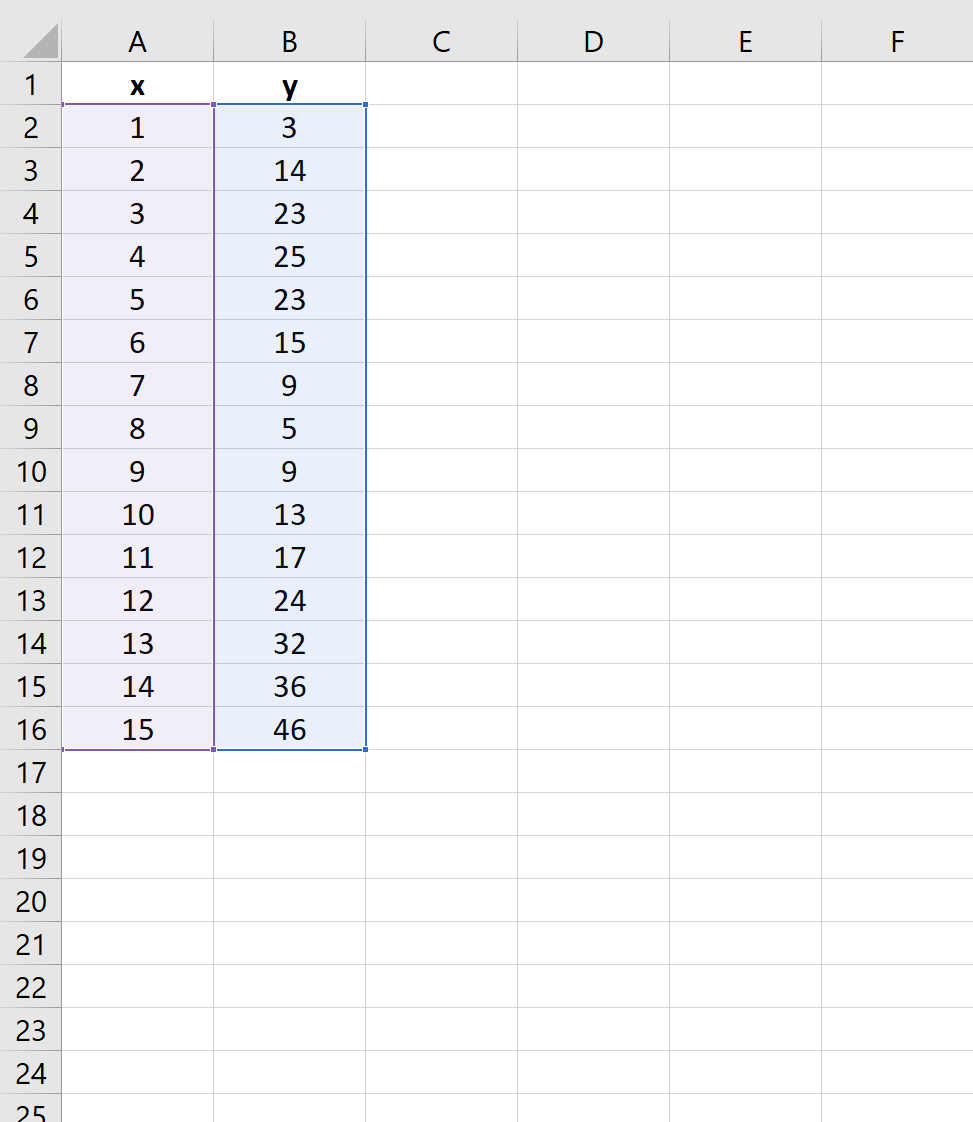
Ensuite, cliquez sur l’onglet Insérer le long du ruban supérieur, puis cliquez sur la première option de tracé sous Scatter :
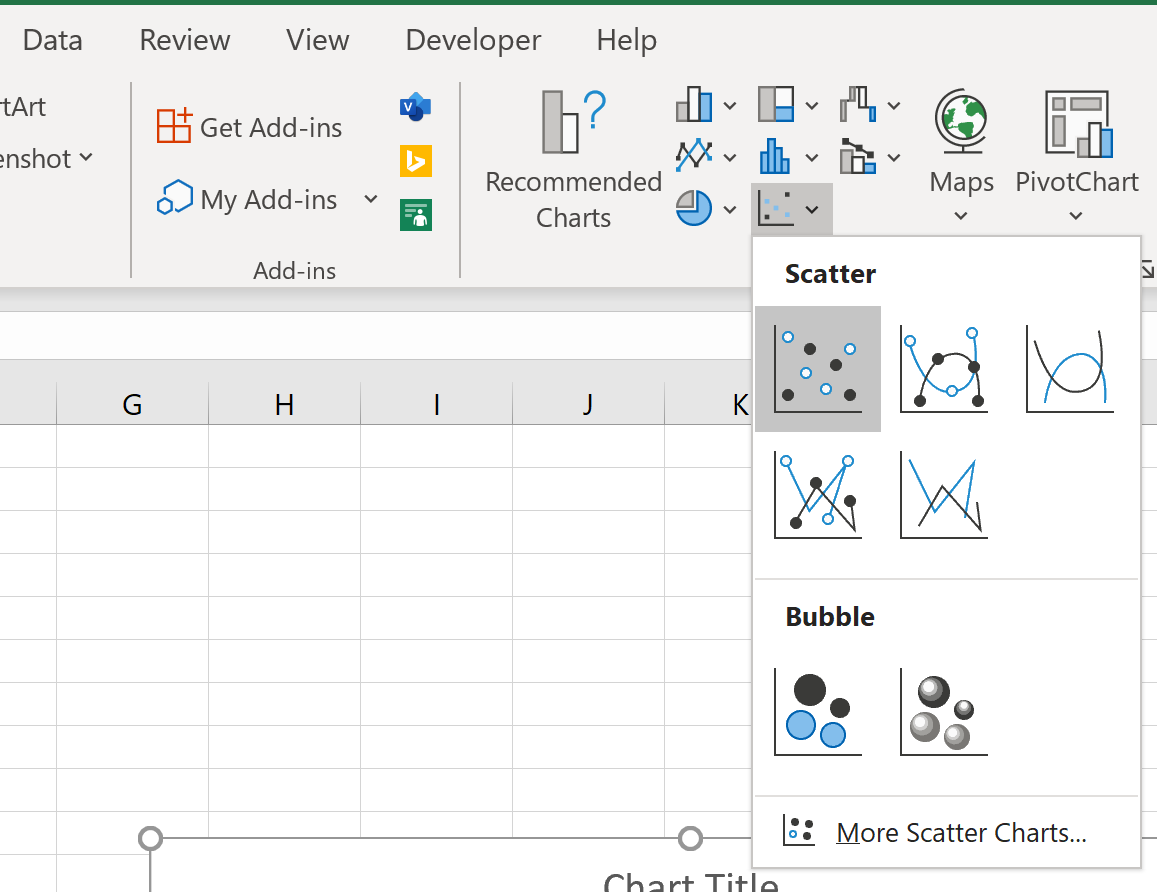
Cela produit le nuage de points suivant :
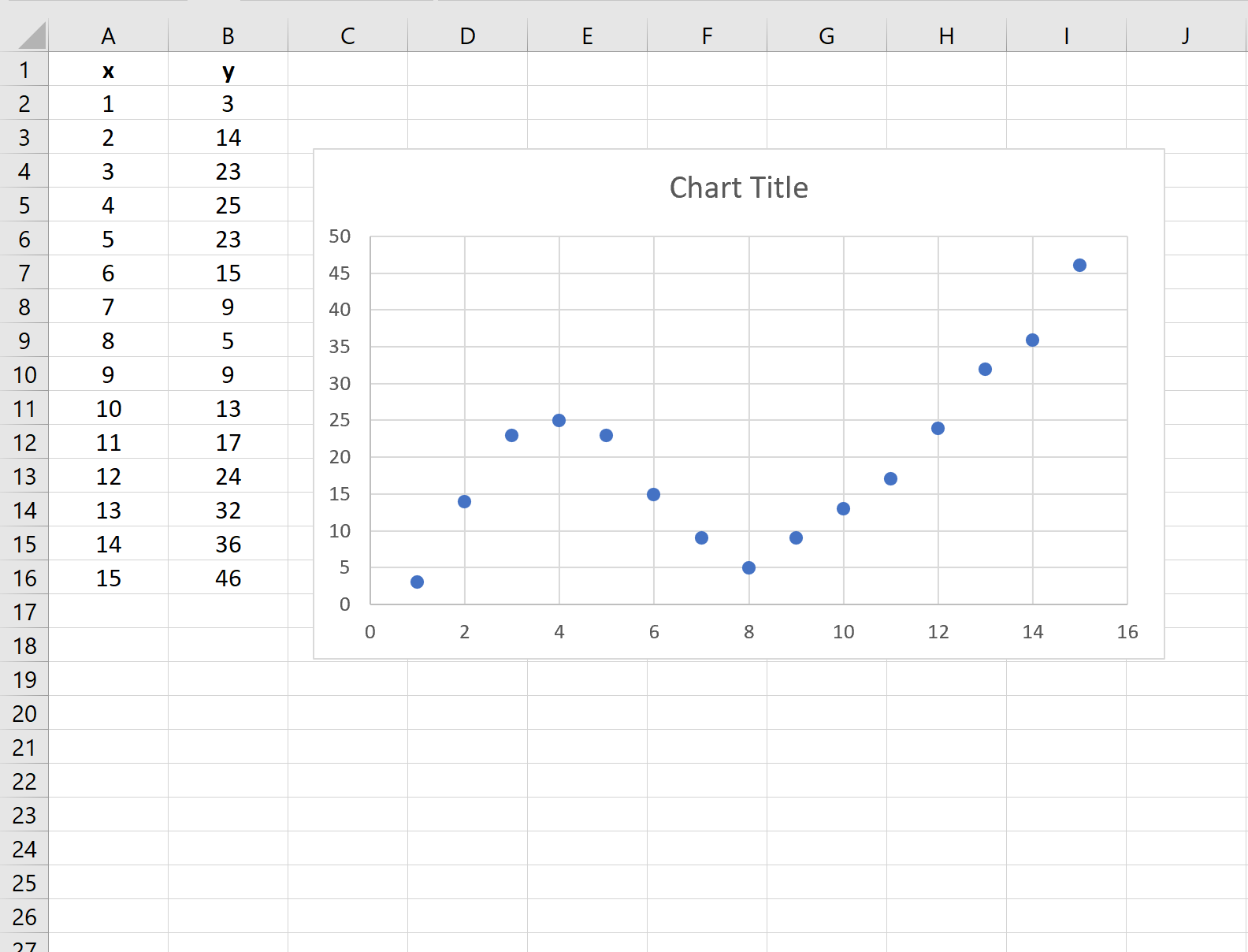
Étape 3 : ajouter une ligne de tendance
Ensuite, cliquez n’importe où sur le nuage de points. Cliquez ensuite sur le signe + dans le coin supérieur droit. Dans le menu déroulant, cliquez sur la flèche à côté de Trendline puis cliquez sur Plus d’options :
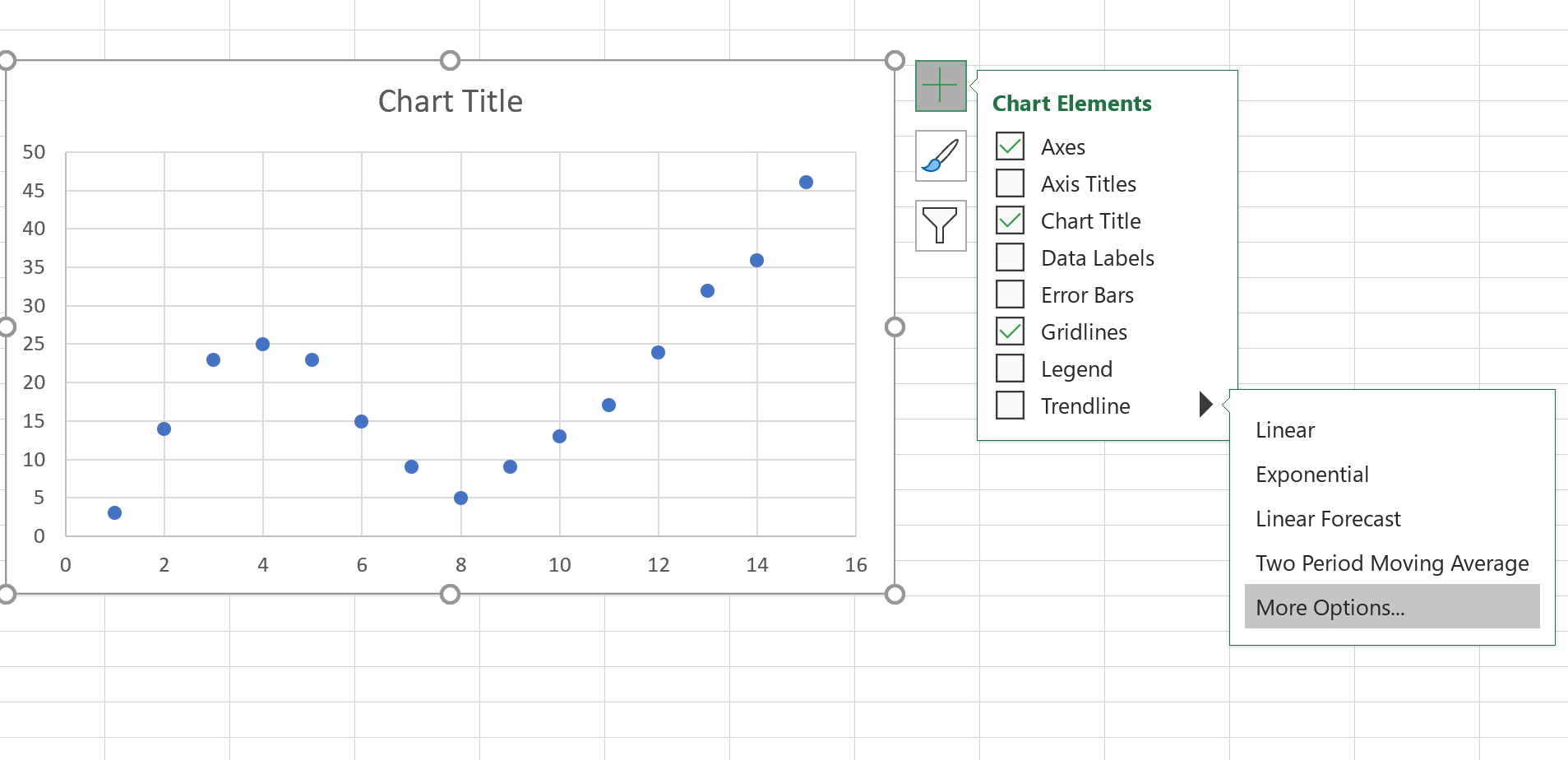
Dans la fenêtre qui apparaît à droite, cliquez sur le bouton à côté de Polynomial . Cochez ensuite les cases à côté de Afficher l’équation sur le graphique et Afficher la valeur R au carré sur le graphique .
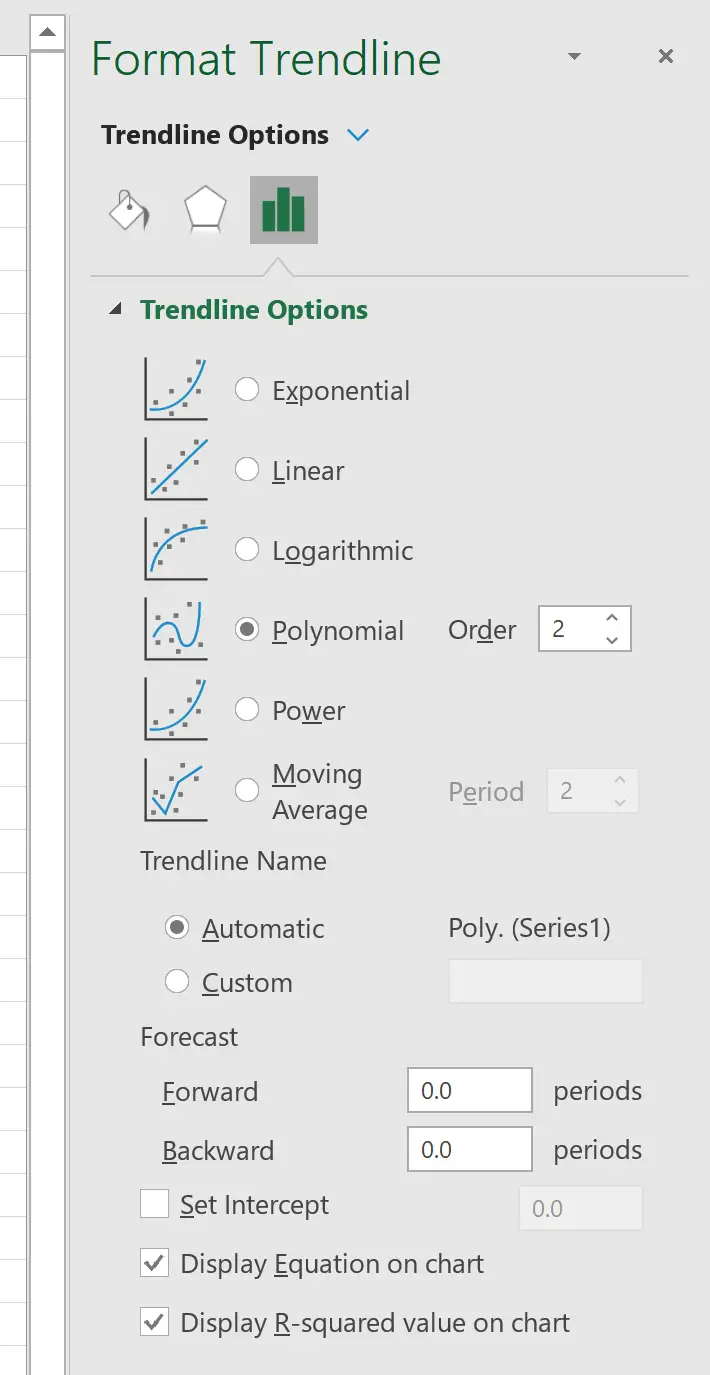
Cela produit la courbe suivante sur le nuage de points :
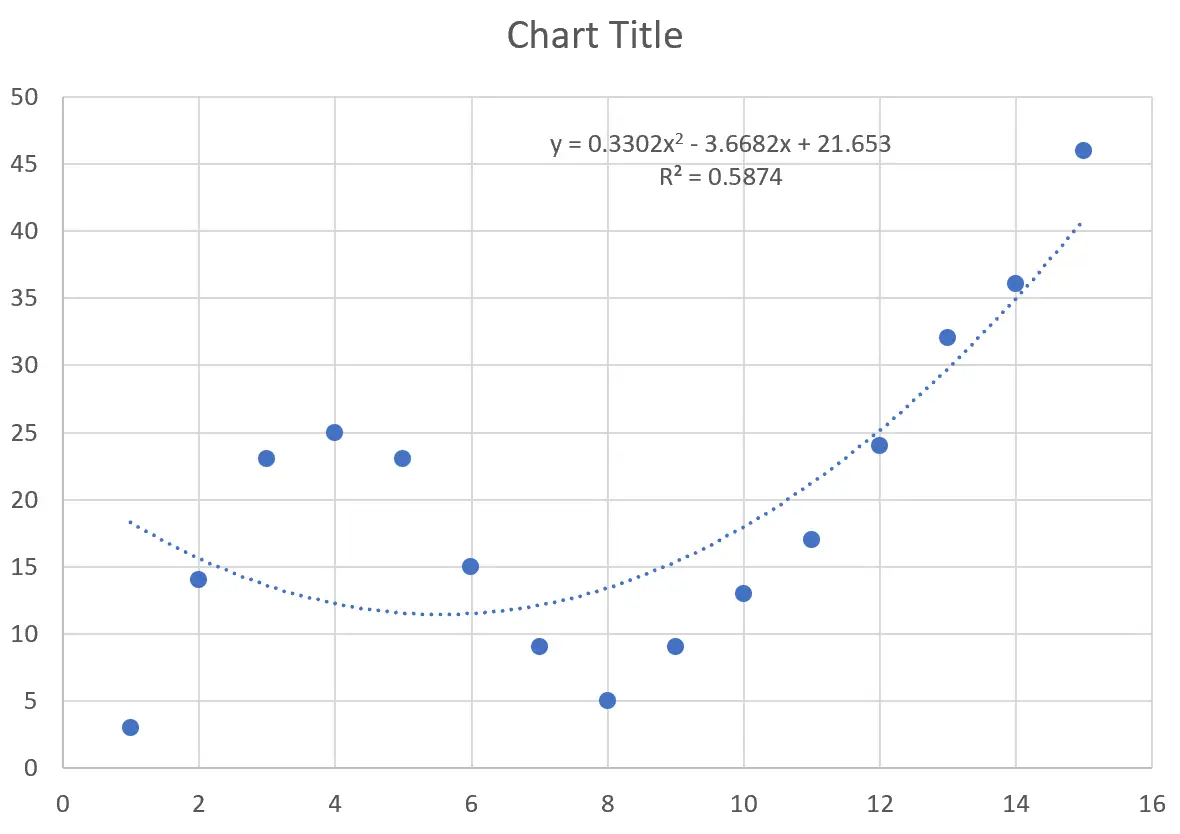
L’équation de la courbe est la suivante :
y = 0,3302x 2 – 3,6682x + 21,653
Le R au carré nous indique le pourcentage de variation de la variable de réponse qui peut être expliqué par les variables prédictives. Le R au carré pour cette courbe particulière est de 0,5874 .
Étape 4 : Choisissez la meilleure ligne de tendance
Nous pouvons également augmenter l’ordre du polynôme que nous utilisons pour voir si une courbe plus flexible permet un meilleur ajustement à l’ensemble de données.
Par exemple, nous pourrions choisir de définir l’ordre polynomial sur 4 :
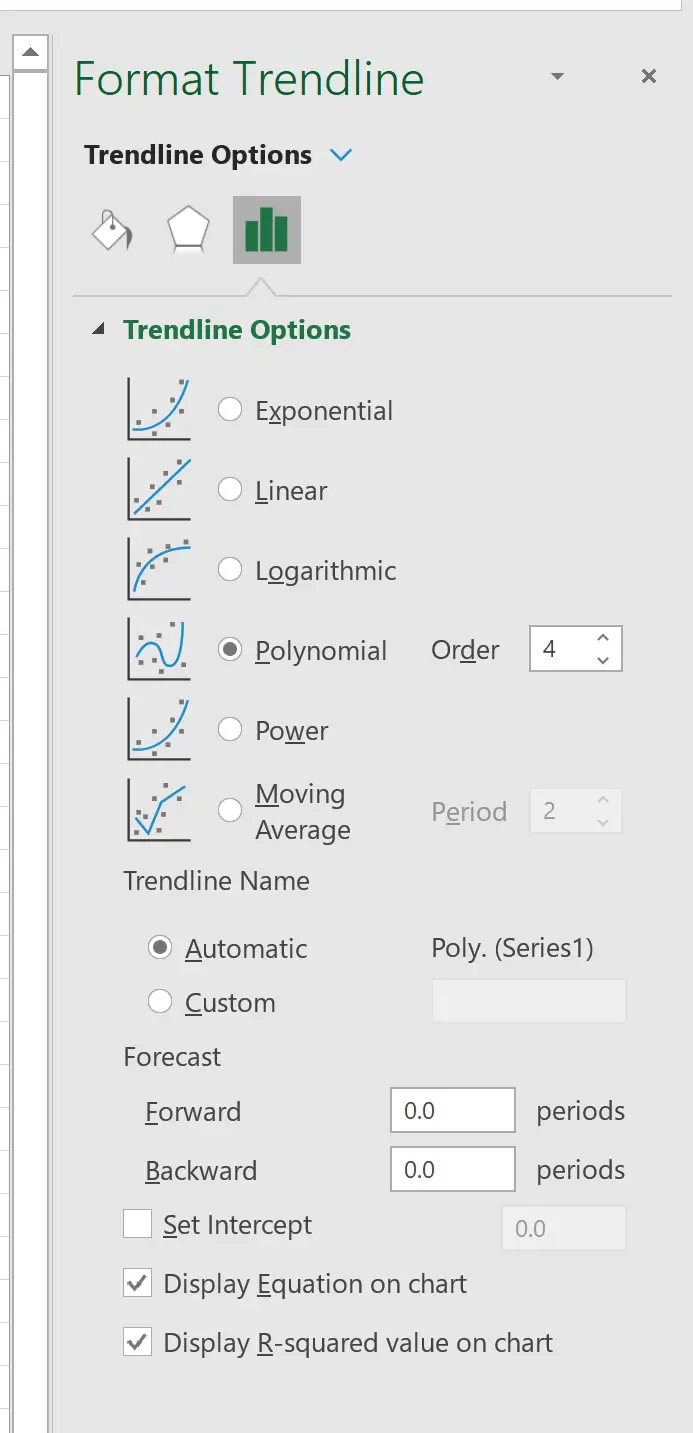
Il en résulte la courbe suivante :
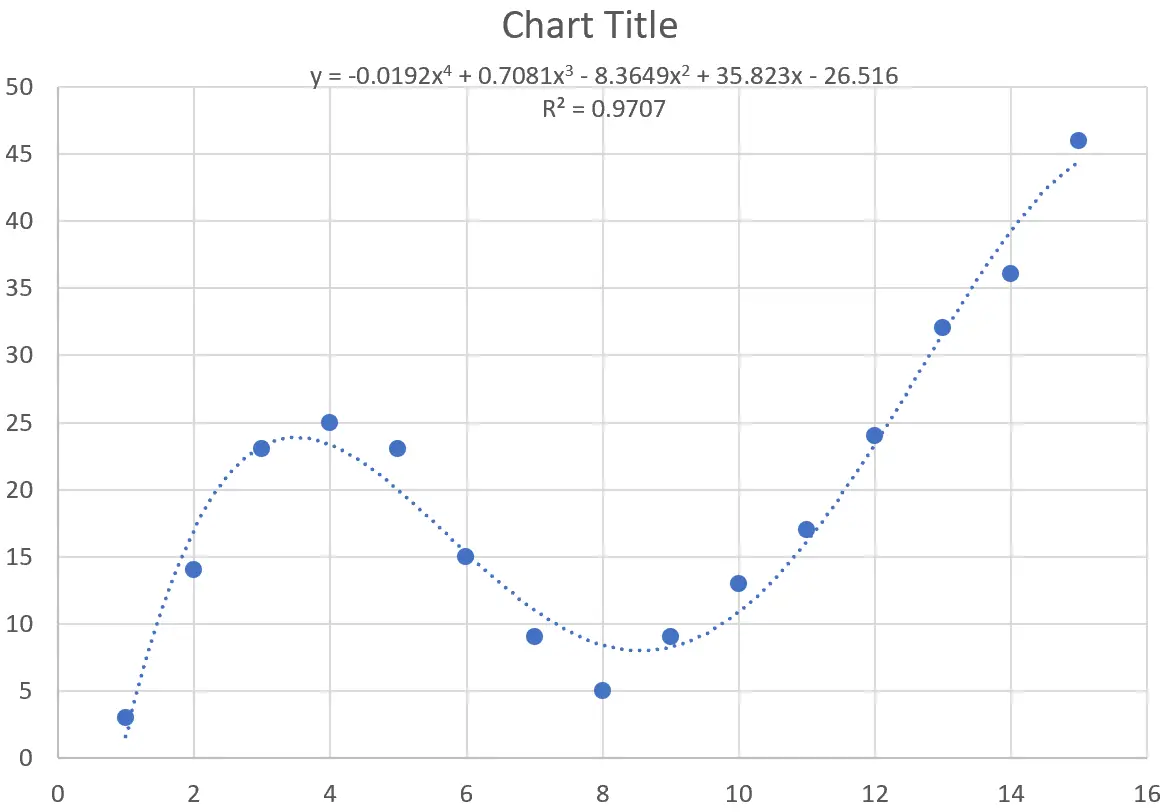
L’équation de la courbe est la suivante :
y = -0,0192x 4 + 0,7081x 3 – 8,3649x 2 + 35,823x – 26,516
Le R au carré pour cette courbe particulière est de 0,9707 .
Ce R au carré est considérablement plus élevé que celui de la courbe précédente, ce qui indique qu’il correspond beaucoup plus étroitement à l’ensemble de données.
Nous pouvons également utiliser cette équation de la courbe pour prédire la valeur de la variable de réponse en fonction de la variable prédictive. Par exemple si x = 4 alors nous prédirions que y = 23,34 :
y = -0,0192(4) 4 + 0,7081(4) 3 – 8,3649(4) 2 + 35,823(4) – 26,516 = 23,34
Vous pouvez trouver plus de didacticiels Excel sur cette page .
