R multiple ou R carré : quelle est la différence ?

Lorsque vous ajustez un modèle de régression à l’aide de la plupart des logiciels statistiques, vous remarquerez souvent les deux valeurs suivantes dans le résultat :

Multiple R : le coefficient de corrélation multiple entre trois variables ou plus.

R-Carré : Ceci est calculé comme (Multiple R) ² et représente la proportion de la variance de la variable de réponse d’un modèle de régression qui peut être expliquée par les variables prédictives. Cette valeur varie de 0 à 1.

En pratique, nous sommes souvent intéressés par la valeur R au carré car elle nous indique l’utilité des variables prédictives pour prédire la valeur de la variable de réponse.

Cependant, chaque fois que nous ajoutons une nouvelle variable prédictive au modèle, le R au carré est assuré d’augmenter même si la variable prédictive n’est pas utile.

Le R-carré ajusté est une version modifiée du R-carré qui s’ajuste au nombre de prédicteurs dans un modèle de régression. Il est calculé comme suit :

R ² ajusté = 1 – [(1-R ² )*(n-1)/(nk-1)]

où:

• R ² : Le R ² du modèle
• n : Le nombre d’observations
• k : Le nombre de variables prédictives

Étant donné que le R-carré augmente toujours à mesure que vous ajoutez davantage de prédicteurs à un modèle, le R-carré ajusté peut servir de mesure qui vous indique l’utilité d’un modèle, ajusté en fonction du nombre de prédicteurs dans un modèle .

Pour mieux comprendre chacun de ces termes, considérons l’exemple suivant.

Exemple : R multiple, R-carré et R-carré ajusté

Supposons que nous ayons l’ensemble de données suivant qui contient les trois variables suivantes pour 12 étudiants différents :

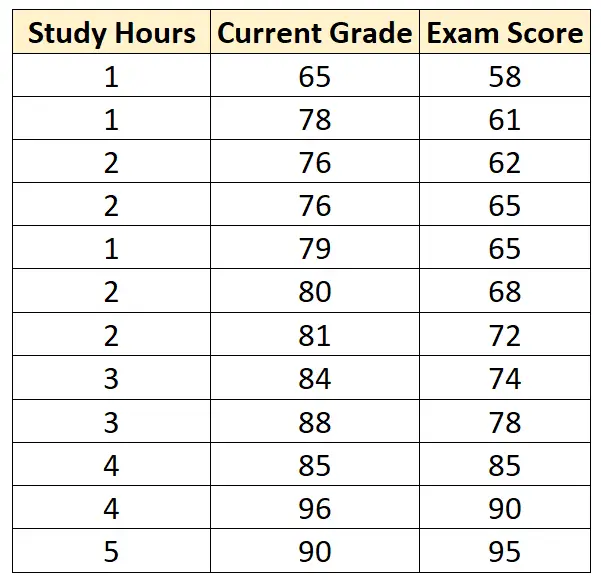
Supposons que nous ajustions un modèle de régression linéaire multiple en utilisant les heures d’étude et la note actuelle comme variables prédictives et le résultat de l’examen comme variable de réponse et que nous obtenions le résultat suivant :

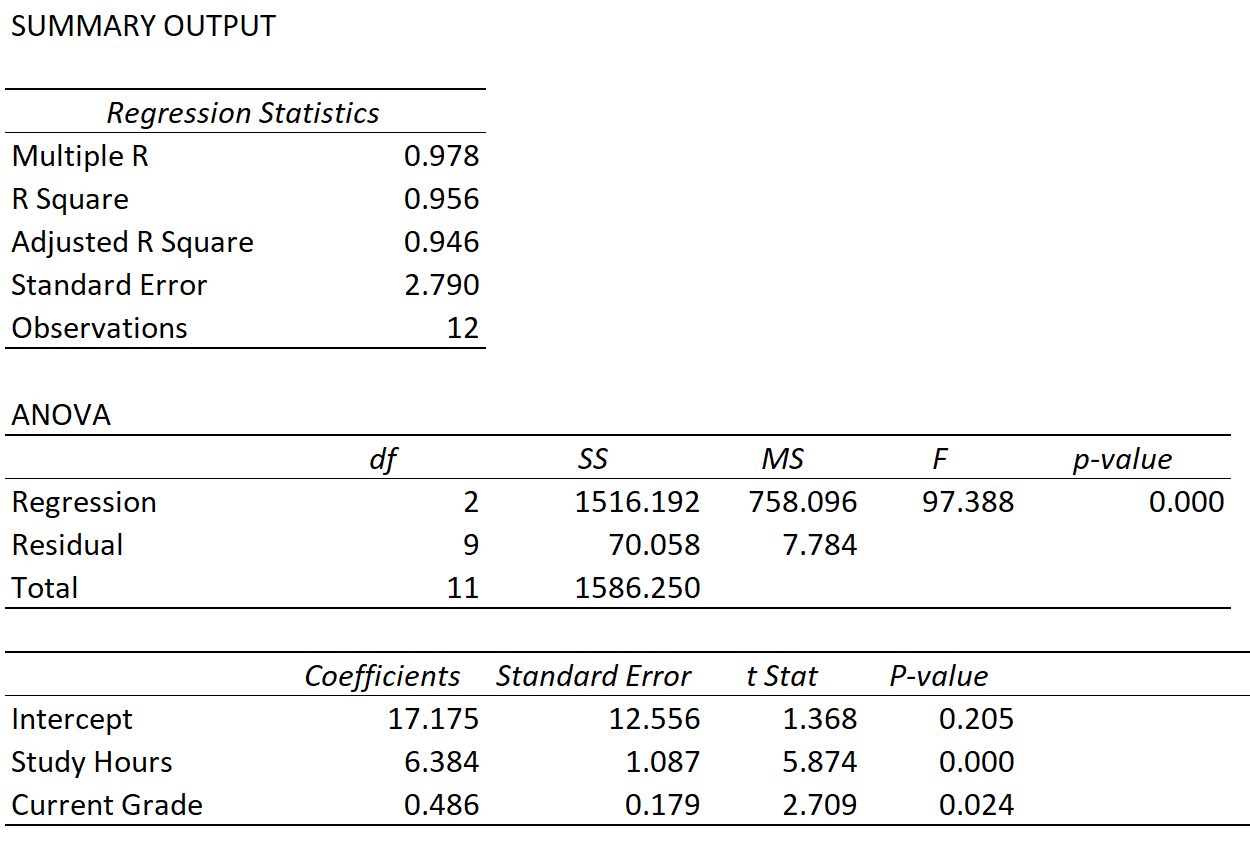
Nous pouvons observer les valeurs des trois métriques suivantes :

R multiples : 0,978 . Cela représente la corrélation multiple entre la variable de réponse et les deux variables prédictives.

R Carré : 0,956 . Ceci est calculé comme (Multiple R) ² = (0,978) ² = 0,956. Cela nous indique que 95,6 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures passées à étudier par l’étudiant et par sa note actuelle dans le cours.

R-carré ajusté : 0,946 . Ceci est calculé comme suit :

R ² ajusté = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0,946.

Cela représente la valeur R au carré, ajustée en fonction du nombre de variables prédictives dans le modèle .

Cette mesure serait utile si, par exemple, nous ajustions un autre modèle de régression avec 10 prédicteurs et constations que le R-carré ajusté de ce modèle était de 0,88 . Cela indiquerait que le modèle de régression avec seulement deux prédicteurs est meilleur car il a une valeur R carré ajustée plus élevée.

Ressources additionnelles

Introduction à la régression linéaire multiple
Qu’est-ce qu’une bonne valeur R au carré ?