Comment calculer l’erreur type de régression dans Excel
Chaque fois que nous ajustons un modèle de régression linéaire , le modèle prend la forme suivante :
Y = β 0 + β 1 X + … + β je X +ϵ
où ϵ est un terme d’erreur indépendant de X.
Quelle que soit la manière dont X peut être utilisé pour prédire les valeurs de Y, il y aura toujours une erreur aléatoire dans le modèle.
Une façon de mesurer la dispersion de cette erreur aléatoire consiste à utiliser l’ erreur standard du modèle de régression , qui est un moyen de mesurer l’écart type des résidus ϵ.
Ce didacticiel fournit un exemple étape par étape de la façon de calculer l’erreur type d’un modèle de régression dans Excel.
Étape 1 : Créer les données
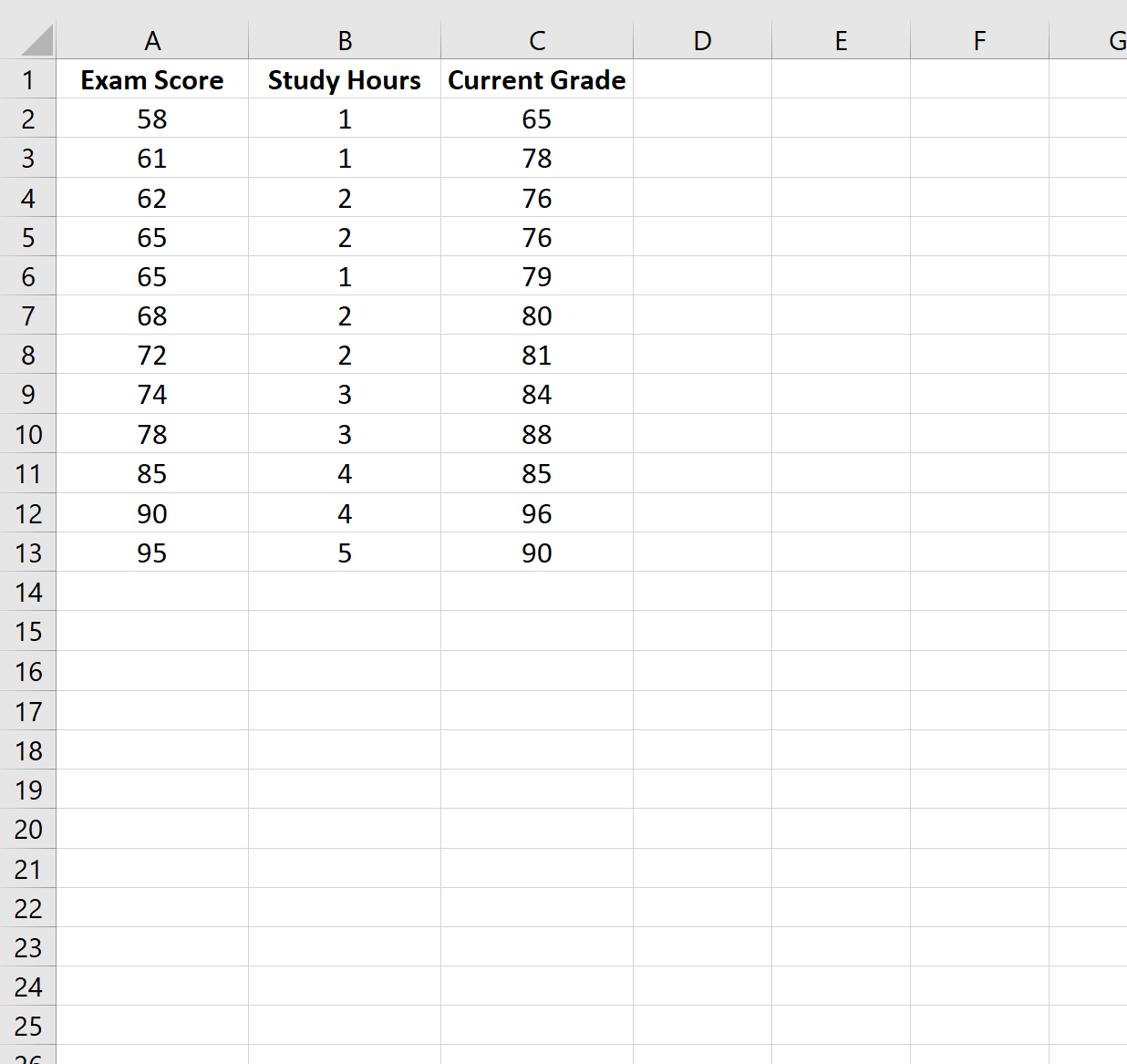
Pour cet exemple, nous allons créer un ensemble de données contenant les variables suivantes pour 12 étudiants différents :
- Résultat de l’examen
- Heures passées à étudier
- Classe actuelle
Étape 2 : Ajuster le modèle de régression
Ensuite, nous ajusterons un modèle de régression linéaire multiple en utilisant le résultat de l’examen comme variable de réponse et les heures d’étude et la note actuelle comme variables prédictives.
Pour ce faire, cliquez sur l’onglet Données le long du ruban supérieur, puis cliquez sur Analyse des données :

Si cette option n’est pas disponible, vous devez d’abord charger le Data Analysis ToolPak .
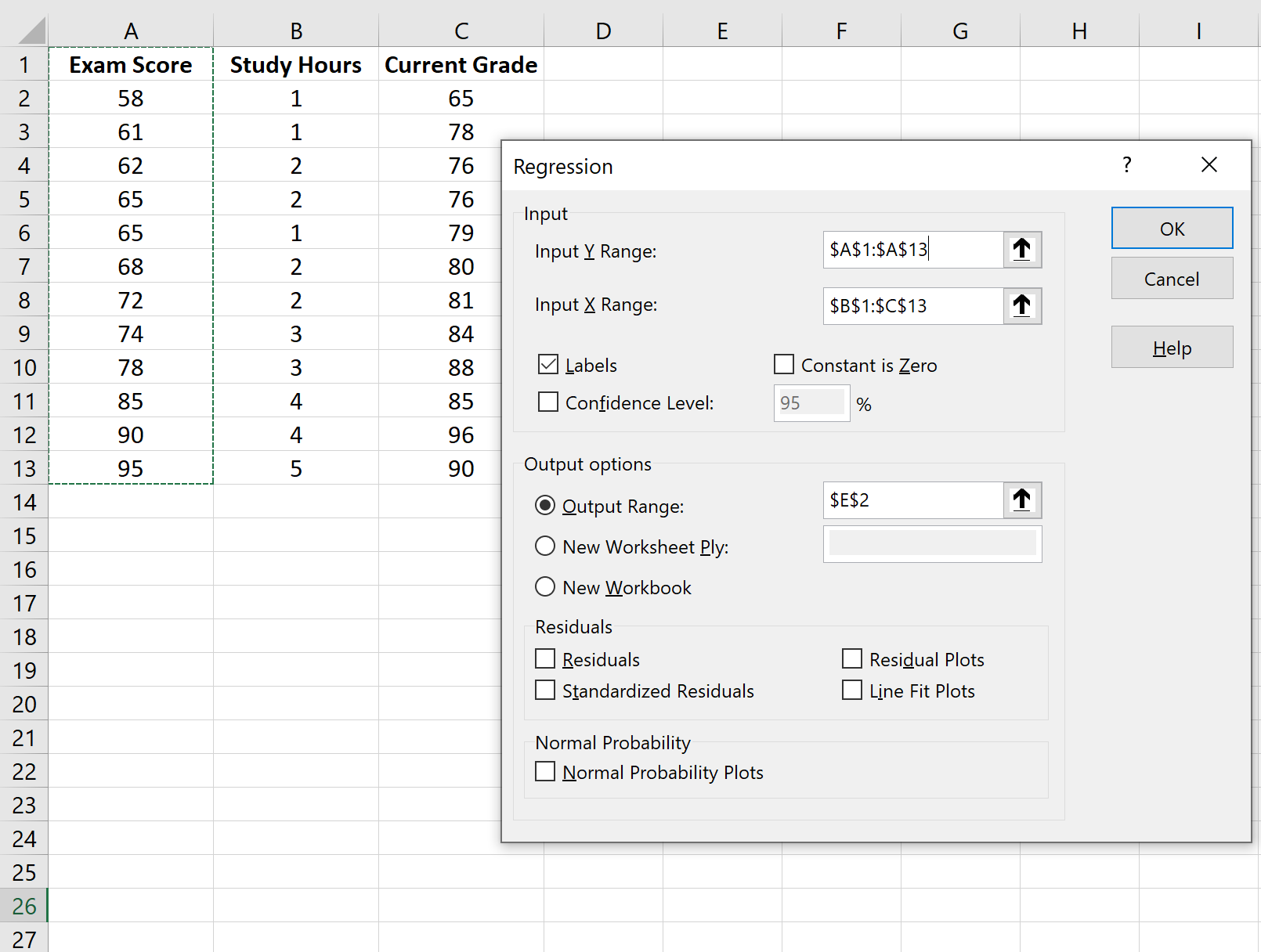
Dans la fenêtre qui apparaît, sélectionnez Régression . Dans la nouvelle fenêtre qui apparaît, renseignez les informations suivantes :
Une fois que vous avez cliqué sur OK , la sortie du modèle de régression apparaîtra :
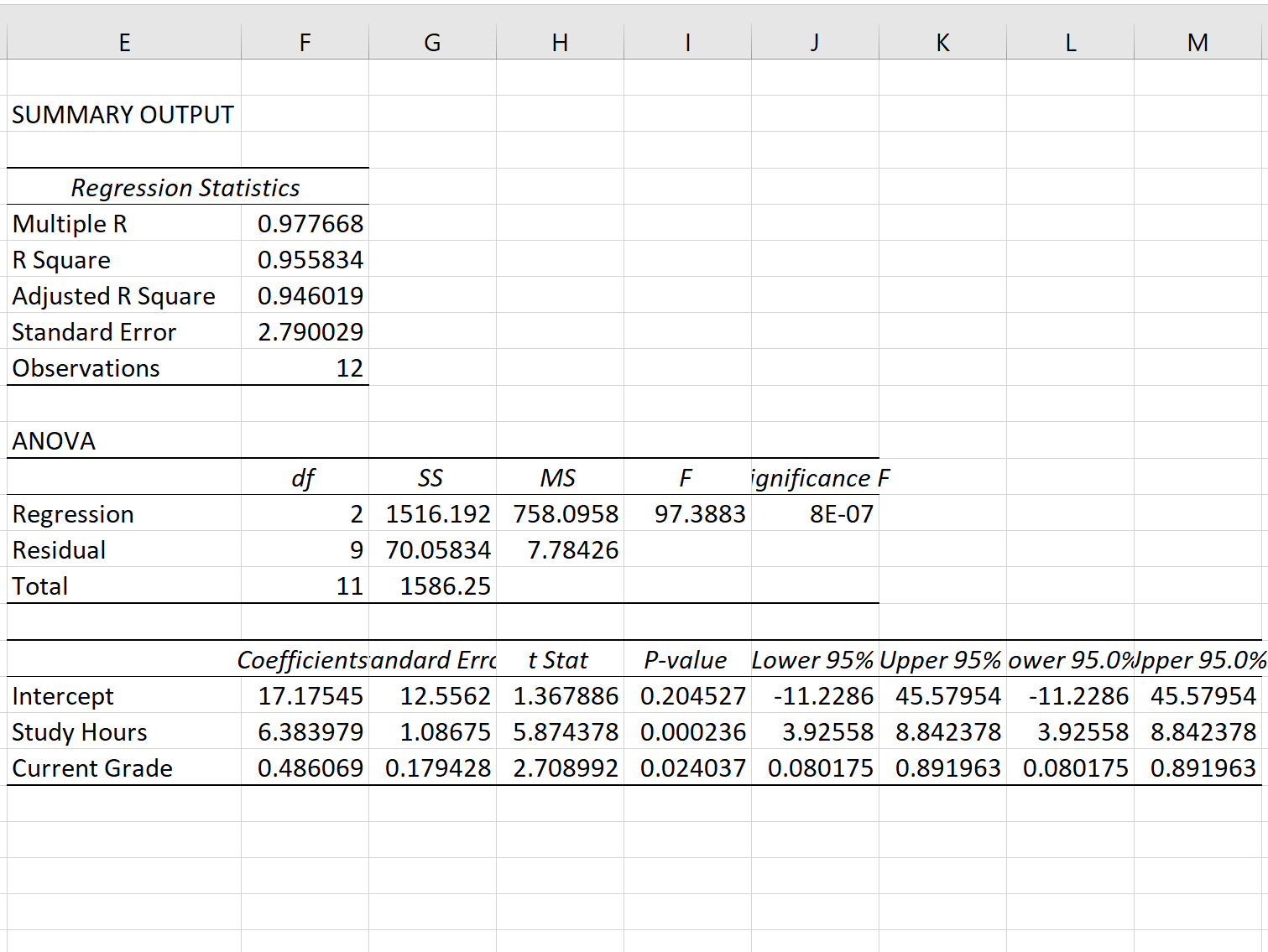
Étape 3 : Interpréter l’erreur type de régression
L’erreur standard du modèle de régression est le nombre à côté de l’erreur standard :
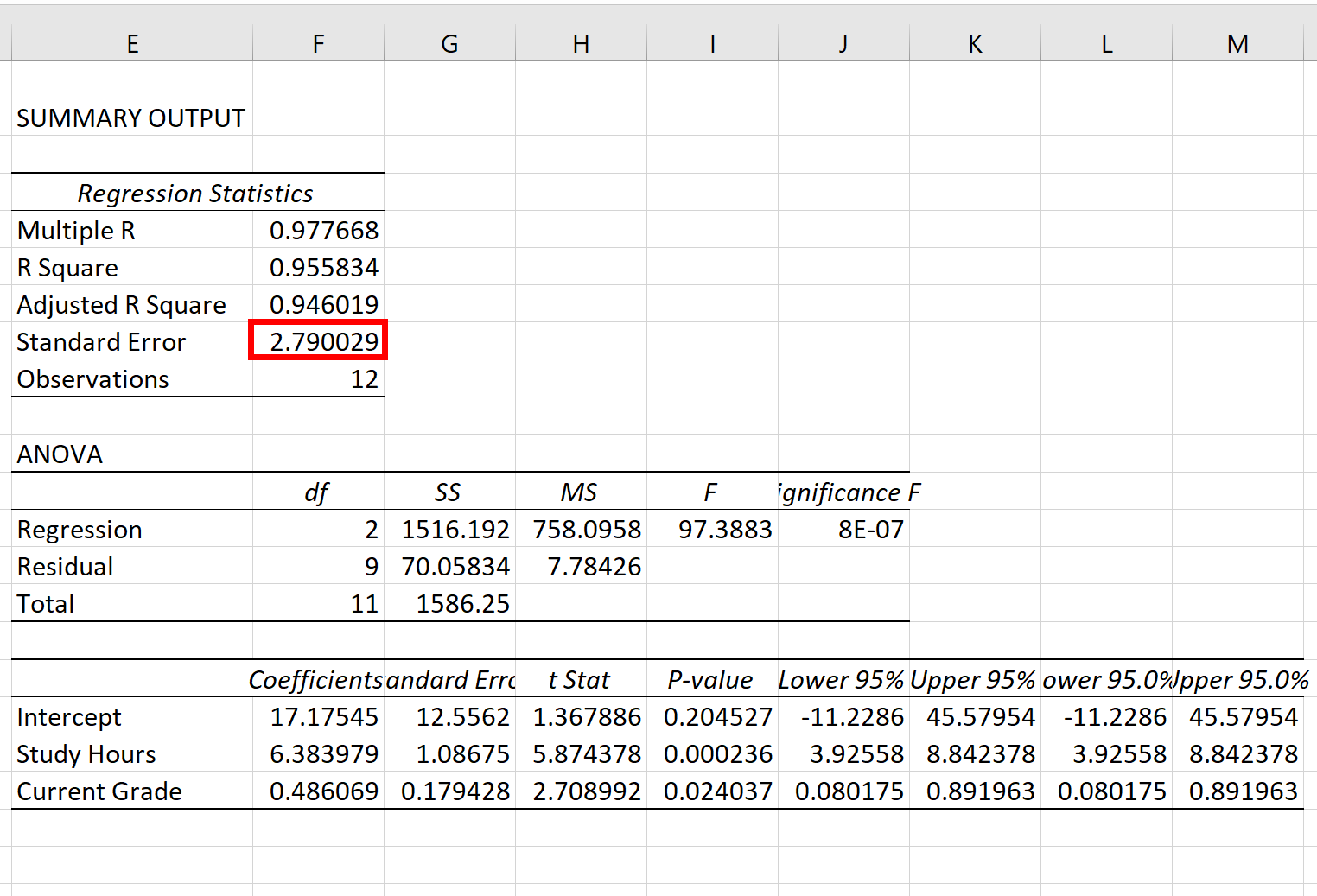
L’erreur type de ce modèle de régression particulier s’avère être de 2,790029 .
Ce nombre représente la distance moyenne entre les résultats réels des examens et les résultats des examens prédits par le modèle.
Notez que certains résultats d’examen seront éloignés de plus de 2,79 unités du score prévu, tandis que d’autres en seront plus proches. Mais, en moyenne, la distance entre les résultats réels des examens et les résultats prévus est de 2,790029 .
Notez également qu’une erreur type de régression plus petite indique qu’un modèle de régression s’adapte plus étroitement à un ensemble de données.
Ainsi, si nous ajustons un nouveau modèle de régression à l’ensemble de données et obtenons une erreur standard de, disons, 4,53 , ce nouveau modèle serait moins efficace pour prédire les résultats aux examens que le modèle précédent.
Ressources additionnelles
Une autre façon courante de mesurer la précision d’un modèle de régression consiste à utiliser le R au carré. Consultez cet article pour une belle explication des avantages de l’utilisation de l’erreur type de la régression pour mesurer la précision par rapport au R-carré.
