Comment utiliser des variables factices dans l’analyse de régression

La régression linéaire est une méthode que nous pouvons utiliser pour quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Nous utilisons généralement la régression linéaire avec des variables quantitatives . Parfois appelées variables « numériques », ce sont des variables qui représentent une quantité mesurable. Les exemples comprennent:

• Nombre de pieds carrés dans une maison
• Taille de la population d’une ville
• Âge d’un individu

Cependant, nous souhaitons parfois utiliser des variables catégorielles comme variables prédictives. Ce sont des variables qui prennent des noms ou des étiquettes et peuvent entrer dans des catégories. Les exemples comprennent:

• Couleur des yeux (par exemple « bleu », « vert », « marron »)
• Sexe (par exemple « homme », « femme »)
• État civil (par exemple « marié », « célibataire », « divorcé »)

Lorsque vous utilisez des variables catégorielles, cela n’a pas de sens d’attribuer simplement des valeurs comme 1, 2, 3 à des valeurs comme « bleu », « vert » et « marron », car cela n’a pas de sens de dire que le vert est double. aussi coloré que le bleu ou que le marron est trois fois plus coloré que le bleu.

Au lieu de cela, la solution consiste à utiliser des variables factices . Il s’agit de variables que nous créons spécifiquement pour l’analyse de régression et qui prennent l’une des deux valeurs suivantes : zéro ou un.

Variables factices : variables numériques utilisées dans l’analyse de régression pour représenter des données catégorielles qui ne peuvent prendre qu’une des deux valeurs : zéro ou un.

Le nombre de variables factices que nous devons créer est égal à k -1 où k est le nombre de valeurs différentes que la variable catégorielle peut prendre.

Les exemples suivants illustrent comment créer des variables factices pour différents ensembles de données.

Exemple 1 : créer une variable factice avec seulement deux valeurs

Supposons que nous disposions de l’ensemble de données suivant et que nous souhaitions utiliser le sexe et l’âge pour prédire le revenu :

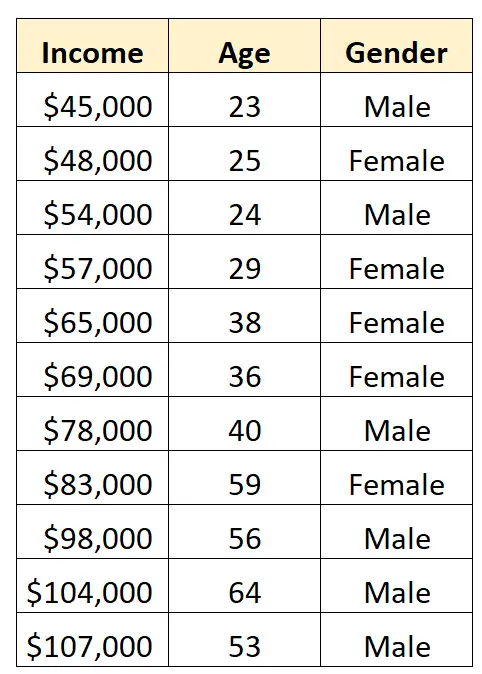
Pour utiliser le sexe comme variable prédictive dans un modèle de régression, nous devons le convertir en variable muette.

Puisqu’il s’agit actuellement d’une variable catégorielle qui peut prendre deux valeurs différentes (« Mâle » ou « Femme »), il suffit de créer k -1 = 2-1 = 1 variable muette.

Pour créer cette variable muette, on peut choisir l’une des valeurs (« Mâle » ou « Femme ») pour représenter 0 et l’autre pour représenter 1.

En général, nous représentons généralement la valeur la plus fréquente avec un 0, ce qui serait « Homme » dans cet ensemble de données.

Ainsi, voici comment convertir le sexe en variable fictive :

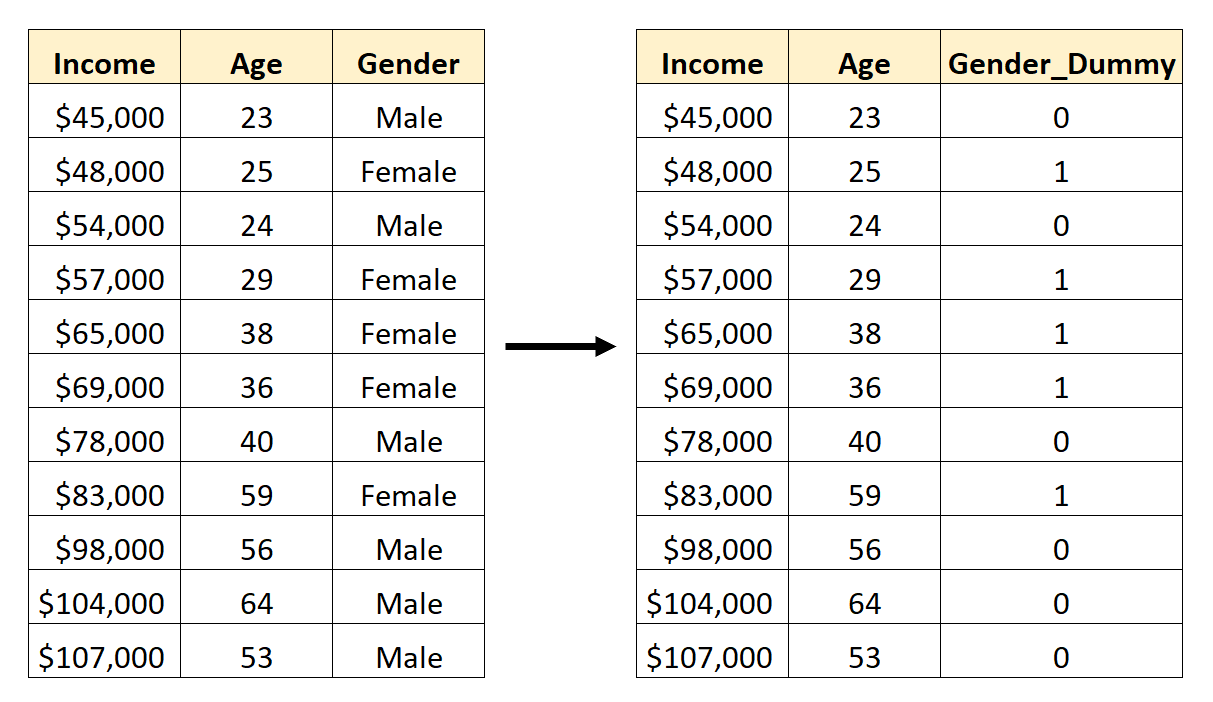
Nous pourrions ensuite utiliser Age et Gender_Dummy comme variables prédictives dans un modèle de régression.

Exemple 2 : créer une variable factice avec plusieurs valeurs

Supposons que nous disposions de l’ensemble de données suivant et que nous souhaitions utiliser l’état civil et l’âge pour prédire le revenu :

Pour utiliser l’état civil comme variable prédictive dans un modèle de régression, nous devons le convertir en variable muette.

Puisqu’il s’agit actuellement d’une variable catégorielle qui peut prendre trois valeurs différentes (« Célibataire », « Marié » ou « Divorcé »), nous devons créer k -1 = 3-1 = 2 variables muettes.

Pour créer cette variable factice, nous pouvons laisser « Single » comme valeur de base car elle apparaît le plus souvent. Ainsi, voici comment nous convertirions l’état civil en variables fictives :

Nous pourrions alors utiliser Age , Marié et Divorcé comme variables prédictives dans un modèle de régression.

Comment interpréter la sortie de régression avec des variables factices

Supposons que nous ajustions un modèle de régression linéaire multiple en utilisant l’ensemble de données de l’exemple précédent avec Age , Married et Divorced comme variables prédictives et Income comme variable de réponse.

Voici le résultat de la régression :

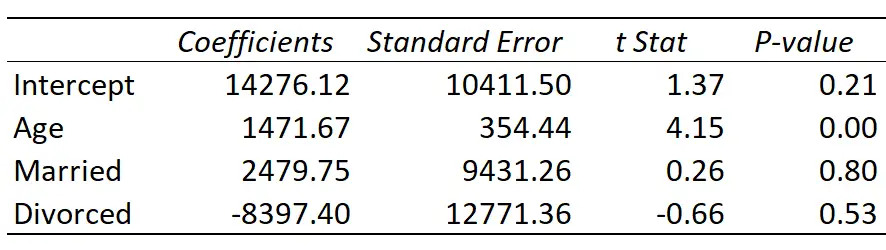
La droite de régression ajustée est définie comme :

Revenu = 14 276,21 + 1 471,67*(Âge) + 2 479,75*(Marié) – 8 397,40*(Divorcé)

Nous pouvons utiliser cette équation pour trouver le revenu estimé d’un individu en fonction de son âge et de son état civil. Par exemple, une personne âgée de 35 ans et mariée aurait un revenu estimé à 68 264 $ :

Revenu = 14 276,21 + 1 471,67*(35) + 2 479,75*(1) – 8 397,40*(0) = 68 264 $

Voici comment interpréter les coefficients de régression du tableau :

• Interception : L’ordonnée à l’origine représente le revenu moyen d’une personne célibataire âgée de zéro an. Évidemment, vous ne pouvez pas avoir zéro an, cela n’a donc aucun sens d’interpréter l’interception par elle-même dans ce modèle de régression particulier.
• Âge : Chaque année d’augmentation de l’âge est associée à une augmentation moyenne de 1 471,67 $ du revenu. Puisque la valeur p (0,00) est inférieure à 0,05, l’âge est un prédicteur statistiquement significatif du revenu.
• Marié : Une personne mariée gagne en moyenne 2 479,75 $ de plus qu’une personne célibataire. Puisque la valeur p (0,80) n’est pas inférieure à 0,05, cette différence n’est pas statistiquement significative.
• Divorcé : Une personne divorcée gagne en moyenne 8 397,40 $ de moins qu’une personne célibataire. Puisque la valeur p (0,53) n’est pas inférieure à 0,05, cette différence n’est pas statistiquement significative.

Étant donné que les deux variables fictives n’étaient pas statistiquement significatives, nous pourrions supprimer l’état matrimonial comme prédicteur du modèle, car il ne semble pas ajouter de valeur prédictive au revenu.

Ressources additionnelles

Variables qualitatives et quantitatives
Le piège variable factice
Comment lire et interpréter un tableau de régression
Une explication des valeurs P et de la signification statistique