Qu’est-ce que le test Q de Cochran ? (Définition & #038; Exemple)
Le test Q de Cochran est un test statistique utilisé pour déterminer si la proportion de « réussites » est égale dans trois groupes ou plus dans lesquels les mêmes individus apparaissent dans chaque groupe.
Par exemple, nous pouvons utiliser le test Q de Cochran pour déterminer si la proportion d’élèves qui réussissent un test est égale lorsque l’on utilise trois techniques d’étude différentes.

Étapes pour effectuer le test Q de Cochran
Le test Q de Cochran utilise les hypothèses nulles et alternatives suivantes :
Hypothèse nulle (H 0 ) : La proportion de « réussites » est la même dans tous les groupes
Hypothèse alternative (H A ) : La proportion de « réussites » est différente dans au moins un des groupes
La statistique du test est calculée comme suit :
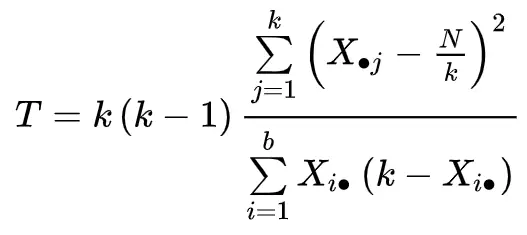
où:
- k : Le nombre de traitements (ou « groupes »)
- Xj : le total de la colonne pour le jème traitement
- b : Le nombre de blocs
- Xi. : Le total de la ligne pour le ième bloc
- N : Le total général
La statistique de test T suit une distribution du Chi carré avec k-1 degrés de liberté.
Si la valeur p associée à la statistique du test est inférieure à un certain niveau de signification (comme α = 0,05), nous pouvons rejeter l’hypothèse nulle et conclure que nous disposons de preuves suffisantes pour affirmer que la proportion de « succès » est différente dans au moins au moins un des groupes.
Exemple : test Q de Cochran
Supposons qu’un chercheur veuille savoir si trois techniques d’étude différentes conduisent à des proportions différentes de taux de réussite parmi les étudiants.
Pour tester cela, elle recrute 20 étudiants qui passent chacun un examen de difficulté égale en utilisant trois techniques d’étude différentes. Les résultats sont montrés plus bas:

Pour effectuer le test Q de Cochran, nous pouvons utiliser un logiciel statistique car il peut être fastidieux à réaliser manuellement.
Voici le code que nous pouvons utiliser pour créer cet ensemble de données et effectuer le test Q de Cochran dans le langage de programmation statistique R :
#load DescTools package library(DescTools) #create dataset df <- data.frame(student=rep(1:20, each=3), technique=rep(c('A', 'B', 'C'), times=20), outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1)) #perform Cochran's Q test CochranQTest(outcome ~ technique| student, data=df) Cochran's Q test data: outcome and technique and student Q = 0.33333, df = 2, p-value = 0.8465
À partir du résultat du test, nous pouvons observer ce qui suit :
- La statistique du test est de 0,333
- La valeur p correspondante est de 0,8465
Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.
Cela signifie que nous n’avons pas suffisamment de preuves pour affirmer que la technique d’étude utilisée par les étudiants conduit à des proportions différentes de taux de réussite.
