Qu’est-ce qu’une distribution catégorielle ?
Une distribution catégorielle est une distribution de probabilité discrète qui décrit la probabilité qu’une variable aléatoire prenne une valeur appartenant à l’une des K catégories, où chaque catégorie est associée à une probabilité.
Pour qu’une distribution soit classée comme distribution catégorielle, elle doit répondre aux critères suivants :
- Les catégories sont discrètes.
- Il existe deux catégories potentielles ou plus.
- La probabilité que la variable aléatoire prenne une valeur dans chaque catégorie doit être comprise entre 0 et 1.
- La somme des probabilités pour toutes les catégories doit totaliser 1.
L’exemple le plus évident de distribution catégorielle est la distribution des résultats associés au lancement d’un dé. Il y a K = 6 résultats potentiels et la probabilité de chaque résultat est de 1/6 :
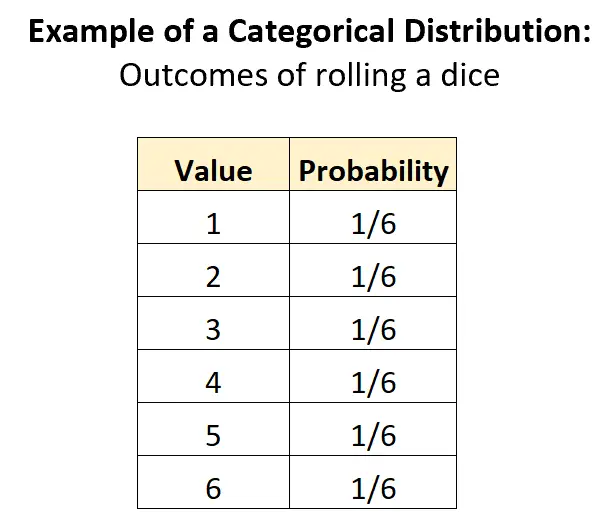
Cette distribution satisfait à tous les critères pour être classée comme distribution catégorielle :
- Les catégories sont discrètes (par exemple la variable aléatoire ne peut prendre que des valeurs discrètes – 1, 2, 3, 4, 5, 6)
- Il existe deux catégories potentielles ou plus.
- La probabilité de chaque catégorie est comprise entre 0 et 1.
- La somme des probabilités totalise 1 : 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.
Règle générale :
Si vous pouvez compter le nombre de résultats, alors vous travaillez avec une variable aléatoire discrète – par exemple, compter le nombre de fois qu’une pièce tombe sur face.
Mais si vous pouvez mesurer le résultat, vous travaillez avec une variable aléatoire continue – par exemple mesurer la taille, le poids, le temps, etc.
Autres exemples de distributions catégorielles
Il existe de nombreuses distributions catégorielles dans le monde réel, notamment :
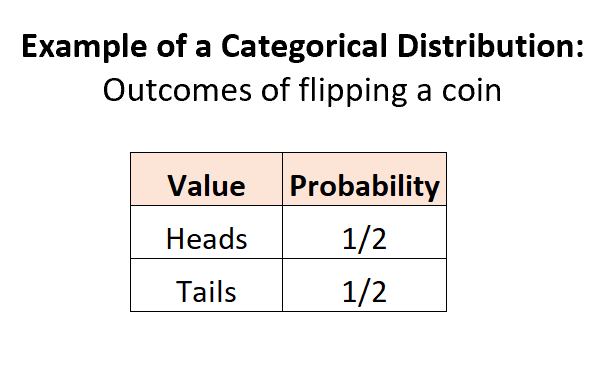
Exemple 1 : lancer une pièce.
Lorsque nous tirons à pile ou face, il y a 2 résultats discrets potentiels, la probabilité de chaque résultat est comprise entre 0 et 1, et la somme des probabilités est égale à 1 :
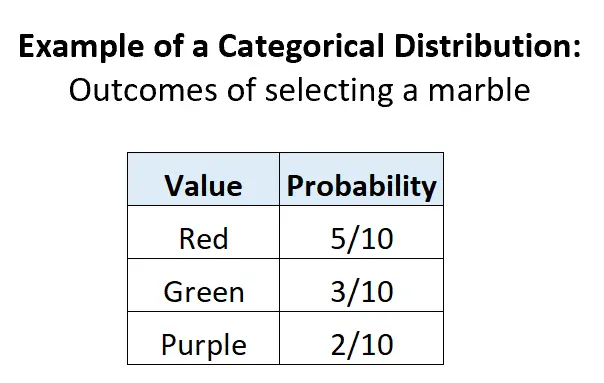
Exemple 2 : Sélection de billes dans une urne.
Supposons qu’une urne contienne 5 billes rouges, 3 billes vertes et 2 billes violettes. Si nous sélectionnons au hasard une bille de l’urne, il y a 3 résultats discrets potentiels, la probabilité de chaque résultat est comprise entre 0 et 1, et la somme des probabilités est égale à 1 :
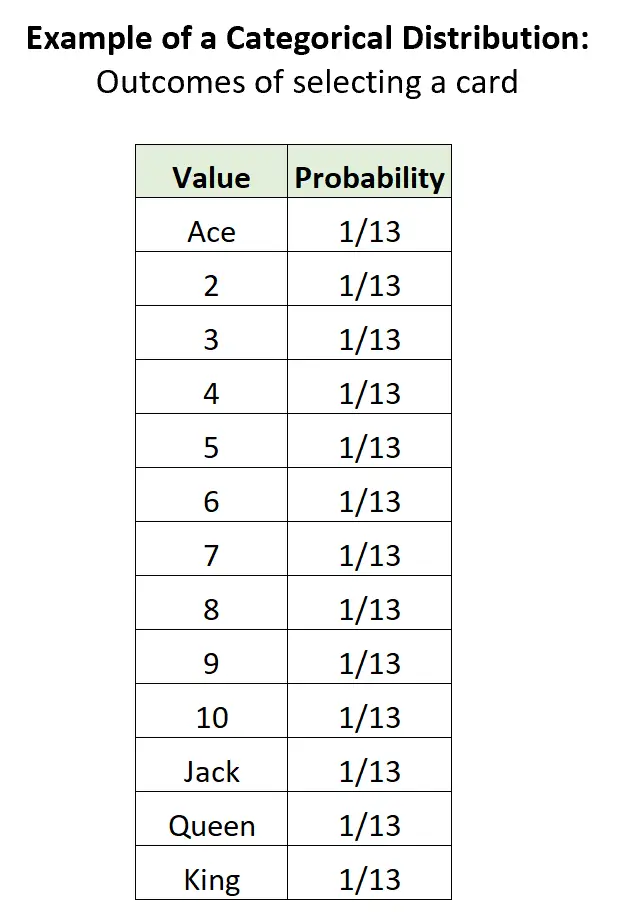
Exemple 3 : Sélection d’une carte dans un deck.
Si nous sélectionnons au hasard une carte dans un jeu standard de 52 cartes, il existe 13 résultats discrets potentiels, la probabilité de chaque résultat est comprise entre 0 et 1, et la somme des probabilités est égale à 1 :
Relation avec d’autres distributions
Pour qu’une distribution soit classée comme distribution catégorielle , elle doit avoir K ≥ 2 résultats potentiels et n = 1 essai.
En utilisant cette terminologie, une distribution catégorielle est similaire aux distributions suivantes :
Distribution de Bernoulli : K = 2 résultats, n = 1 essai
Distribution binomiale : K = 2 critères de jugement, n ≥ 1 essai
Distribution multinomiale : K ≥ 2 résultats, n ≥ essai
Ressources additionnelles
Que sont les variables aléatoires ?
Une introduction à la distribution binomiale
Une introduction à la distribution multinomiale
